giúp e vs ạ

giúp e vs ạ

a)
\(=2y\left(10y-3\right)+15\left(10y-3\right)\\ =\left(10y-3\right)\left(2y+15\right)\)
b)
\(=3x\left(x-7y\right)-24\left(x-7y\right)\\ =\left(x-7y\right)\left(3x-24\right)\)
\(=3\left(x-7y\right)\left(x-8\right)\)
c)
\(=21x\left(4x+5\right)+9\left(4x+5\right)\\ =\left(4x+5\right)\left(21x+9\right)\\ =3\left(4x+5\right)\left(7x+3\right)\)
d)
\(=12\left(x-5\right)+5y\left(5-x\right)\\ =12\left(x-5\right)-5y\left(x-5\right)\\ =\left(x-5\right)\left(12-5y\right)\)
e)
\(=5x\left(2y-z\right)+x^2\left(2y-z\right)\\ =\left(2y-z\right)\left(5x+x^2\right)\\ =x\left(2y-z\right)\left(5+x\right)\)
f)
\(=2xy\left(y-3z\right)-10x\left(3z-y\right)\\ =2xy\left(y-3z\right)+10x\left(y-3z\right)\\ =\left(y-3z\right)\left(2xy+10x\right)\\ =2x\left(y-3z\right)\left(y+5\right)\)
`HaNa☘D`
a) \(2y\left(10y-3\right)-15\left(3-10y\right)\)
\(=2y\left(10y-3\right)+15\left(10y-3\right)\)
\(=\left(10y-3\right)\left(2y-15\right)\)
b) \(3x\left(x-7y\right)+24\left(7y-x\right)\)
\(=3x\left(x-7y\right)-24\left(x-7y\right)\)
\(=3\left(x-7y\right)\left(x-8\right)\)
c) \(21x\left(4x+5\right)+36x+45\)
\(=21x\left(4x+5\right)+9\left(4x+5\right)\)
\(=3\left(7x+3\right)\left(4x+5\right)\)
d) \(12x-60+5y\left(5-x\right)\)
\(=12\left(x-5\right)-5y\left(x-5\right)\)
\(=\left(x-5\right)\left(12-5y\right)\)
e) \(5x\left(2y-z\right)+2x^2y+x^2z\)
\(=5x\left(2y-z\right)+x^2\left(2y+z\right)\)
\(=x\left(x+5\right)\left(2y-z\right)\)
f) \(2xy^2-6xyz-10x\left(3z-y\right)\)
\(=2xy\left(y-3z\right)+10x\left(y-3z\right)\)
\(=2x\left(y-3z\right)\left(y+5\right)\)
Cho x-y=8 và xy=20 . Tính (x+y)^2
(x+y)^2=(x-y)^2+4xy
=8^2+4*20
=64+80
=144
1) 4x³ - 16x
= 4x(x² - 4)
= 4x(x - 2)(x + 2)
2) x⁴ - y⁴
= (x² - y²)(x² + y²)
= (x - y)(x + y)(x² + y²)
3) x² - 6x + 9 - y²
= (x² - 6x + 9) - y²
= (x - 3)² - y²
= (x - y - 3)(x + y - 3)
4) x² - 4x - 5
= x² - 4x + 4 - 9
= (x² - 4x + 4) - 3²
= (x - 2)² - 3²
= (x - 2 - 3)(x - 2 + 3)
= (x - 5)(x + 1)
5) x² - 9x + 20
= x² - 4x - 5x + 20
= (x² - 4x) - (5x - 20)
= x(x - 4) - 5(x - 4)
= (x - 4)(x - 5)
6) xy² + x²y + 1/4 y³
= y(x² + xy + 1/4 y²)
= y(x + y/2)²
7) x³ - y⁶
= x³ - (y²)³
= (x - y²)(x² + xy² + y⁴)
8) x² + 2xy - 4x - 8y
= (x² + 2xy) - (4x + 8y)
= x(x + 2y) - 4(x + 2y)
= (x + 2y)(x - 4)
9) 3x² + 3x - 6
= 3(x² + x - 6)
= 3(x² - 2x + 3x - 6)
= 3[(x² - 2x) + (3x - 6)]
= 3[x(x - 2) + 3(x - 2)]
= 3(x - 2)(x + 3)
10) 3x² - 4x - 7
= 3x² + 3x - 7x - 7
= (3x² + 3x) - (7x - 7)
= 3x(x + 1) - 7(x + 1)
= (x + 1)(3x - 7)
11) Ta có:
49y² + 28y + 4
= (7y)² + 2.7y.2 + 2²
= (7y + 2)²
Vậy độ dài cạnh hình vuông là 7y + 2
Tìm giá trị lớn nhất : -x^2-4x-5
\(-x^2-4x-5\\ =-\left(x^2+4x+5\right)\\ =-\left(x^2+4x+4+1\right)\\ =-\left(x^2+2.2x+2^2+1\right)\\ =-\left(x^2+2.2x+2^2\right)-1\\ =-\left(x+2\right)^2-1\le-1\)
Giá trị của biểu thức \(-x^2-4x-5\) đạt max khi và chỉ khi \(-\left(x+2\right)^2=0\Leftrightarrow\left(x+2\right)^2=0\Leftrightarrow x+2=0\Leftrightarrow x=-2\)
`HaNa☘D`
-x^2-4x-5
=-(x^2+4x+5)
=-(x^2+4x+4+1)
=-(x+2)^2-1<=-1
Dấu = xảy ra khi x=-2
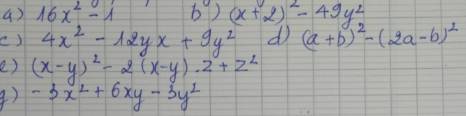
cho tôi xin đáp án nhanh nhất có thể nha!!!
a) \(16x^2-1\)
\(=\left(4x\right)^2-1^2\)
\(=\left(4x-1\right)\left(4x+1\right)\)
b) \(\left(x+2\right)^2-49y^2\)
\(=\left(x+2\right)^{^2}-\left(7y\right)^2\)
\(=\left[\left(x+2\right)-7y\right]\left[\left(x+2\right)+7y\right]\)
\(=\left(x+2-7y\right)\left(x+2+7y\right)\)
c) \(4x^2-12xy+9y^2\)
\(=\left(2x\right)^2-2\cdot2x\cdot3y+\left(3y\right)^2\)
\(=\left(2x-3y\right)^2\)
d) \(\left(a+b\right)^2-\left(2a-b\right)^2\)
\(=\left[\left(a+b\right)+\left(2a-b\right)\right]\left[\left(a+b\right)-\left(2a-b\right)\right]\)
\(=\left(a+b+2a-b\right)\left(a+b-2a+b\right)\)
\(=3a\cdot\left(2b-a\right)\)
e) \(\left(x-y\right)^2-2\left(x-y\right)z+z^2\)
\(=\left[\left(x-y\right)-z\right]^2\)
\(=\left(x-y-z\right)^2\)
g) \(-3x^2+6xy-3y^2\)
\(=-\left(3x^2-6xy+3y^2\right)\)
\(=-3\left(x^2-2xy+y^2\right)\)
\(=-3\left(x-y\right)^2\)
a: 16x^2-1=(4x)^2-1=(4x-1)(4x+1)
b: (x+2)^2-49y^2
=(x+2)^2-(7y)^2
=(x+2+7y)(x+2-7y)
c: 4x^2-12xy+9y^2=(2x-3y)^2
d: (a+b)^2-(2a-b)^2
=(a+b+2a-b)(a+b-2a+b)
=(2b-a)*3a
g: =-3(x^2-2xy+y^2)
=-3(x-y)^2

cho tôi xin đáp án nhanh nhất có thể nha
\(a,6a^2b+9ab^2\)
\(=3ab\left(2a+3b\right)\)
\(b,5x^3y^2-15x^2y^3\)
\(=5x^2y^2\left(x-3y\right)\)
\(c,2x\left(x+1\right)-3y\left(x+1\right)\)
\(=\left(x+1\right)\left(2x-3y\right)\)
\(d,\left(x-y\right)^2-x\left(x-y\right)\)
\(=\left(x-y\right)\left(x-y-x\right)\)
\(=-y\left(x-y\right)\)
\(e,y\left(x-1\right)-x\left(1-x\right)\)
\(=y\left(x-1\right)+x\left(x-1\right)\)
\(=\left(x-1\right)\left(y+x\right)\)
\(g,2a\left(a-b\right)+2b\left(b-a\right)\)
\(=2a\left(a-b\right)-2b\left(a-b\right)\)
\(=\left(2a-2b\right)\left(a-b\right)\)
\(=2\left(a-b\right)^2\)
#Urushi☕
a: 6a^2b+9ab^2
=3ab*2a+3ab*3b
=3ab(2a+3b)
b: 5x^3y^2-15x^2y^3
=5x^2y^2*x-5x^2y^2*3y
=5x^2y^2(x-3y)
c: 2x(x+1)-3y(x+1)
=(x+1)(2x-3y)
d: =(x-y)(x-y-x)
=-y(x-y)
e: =y(x-1)+x(x-1)
=(x-1)(x+y)
g: =2a(a-b)-2b(a-b)
=(a-b)(2a-2b)
=2(a-b)^2
a)\(6a^2b+9ab^2\)=ab(6a+9b)
b)\(5x^3y^2-15x^2y^3\)=5\(x^2y^2\)(x-3y)
c)2x(x+1)-3y(x+1)=(x+1)(2x-3y)
d)\(\left(x-y\right)^2-x\left(x-y\right)\)=(x-y)(x-y-x)
e)y(x-1)-x(1-x)=(x-1)(y+x)
g)2a(a-b)+2b(b-a)=(a-b)(2a-2b)
Phân tích đa thức thành phân tử
7x-6x^2-2
`#040911`
`7x - 6x^2 - 2`
`= -6x^2 + 3x + 4x - 2`
`= -(6x^2 - 3x) + (4x - 2)`
`= -3x(2x - 1) + 2(2x - 1)`
`= (-3x + 2)(2x - 1)`
=-6x^2+3x+4x-2
=-3x(2x-1)+2(2x-1)
=(2x-1)(-3x+2)

hẹp mi với ạ
Bài 5:
a)
\(x^4+x^3+x+1\\ =x^3\left(x+1\right)+\left(x+1\right)\\ =\left(x^3+1\right)\left(x+1\right)\)
b)
\(x^4-x^3-x+1\\ =x^3\left(x-1\right)-\left(x-1\right)\\ =\left(x^3-1\right)\left(x-1\right)\\ =\left(x-1\right)\left(x^2+x+1\right)\left(x-1\right)\)
c)
\(3x^2-12y^2\\ =\left(\sqrt{3}x\right)^2-\left(\sqrt{12}y\right)^2\\ =\left(\sqrt{3}x-\sqrt{12}y\right)\left(\sqrt{3}x+\sqrt{12}y\right)\\ =\sqrt{3}\left(x-\sqrt{4}y\right).\sqrt{3}\left(x+\sqrt{4}y\right)\\ =3\left(x-\sqrt{4}y\right)\left(x+\sqrt{4}y\right)\)
7:
a: (2x-1)^2-25=0
=>(2x-1)^2=25
=>2x-1=-5 hoặc 2x-1=5
=>2x=6 hoặc 2x=-4
=>x=-2 hoặc x=3
b: 8x^3-50x=0
=>4x^3-25x=0
=>x(4x^2-25)=0
=>x(2x-5)(2x+5)=0
=>x=0 hoặc 2x-5=0 hoặc 2x+5=0
=>x=0;x=5/2;x=-5/2
c: 3x(x-1)+(x-1)=0
=>(x-1)(3x+1)=0
=>x=1 hoặc x=-1/3
d: =>2(x+3)-x(x+3)=0
=>(x+3)(2-x)=0
=>x=-3 hoặc x=2
e: Thiếu vế phải rồi bạn
f: x^3+27+(x+3)(x-9)=0
=>(x+3)(x^2-3x+9)+(x+3)(x-9)=0
=>(x+3)(x^2-3x+9+x-9)=0
=>(x+3)(x^2-2x)=0
=>x(x-2)(x+3)=0
=>\(x\in\left\{0;2;-3\right\}\)
Bài 6:
\(B=\left(x-1\right)x^2-4x\left(x-1\right)+4\left(x-1\right)\\ =\left(x-1\right)\left(x^2-4x+4\right)\\ =\left(x-1\right)\left(x-2\right)^2\)
Thay x = 3 vào biểu thức B, ta có:
\(B=\left(3-1\right)\left(3-2\right)^2=2\cdot1^2=2\)
Đề:Phân tích bằng phương pháp tách một hạng tử thành nhiều hạng tử
10: =x^2-3x-4x+12
=x(x-3)-4(x-3)
=(x-3)(x-4)
11: =x^2-2x-5x+10
=x(x-2)-5(x-2)
=(x-2)(x-5)
12: =x^2+x+5x+5
=x(x+1)+5(x+1)
=(x+1)(x+5)
13: =3x^2-6x+x-2
=3x(x-2)+(x-2)
=(x-2)(3x+1)
14: =2x^2+4x-3x-6
=2x(x+2)-3(x+2)
=(x+2)(2x-3)
15: =7x^2+49x+x+7
=7x(x+7)+(x+7)
=(x+7)(7x+1)
18: =2x^2+4x+x+2
=2x(x+2)+(x+2)
=(x+2)(2x+1)
20: =2(x^2+5x+4)
=2(x+1)(x+4)
Giúp mình với ạ

Bài 1A:
\(a,x^2-xy+x-y\\ =x\left(x-y\right)+\left(x-y\right)\\ =\left(x+1\right)\left(x-y\right)\\ b,xz+yz+4x+4y\\ =z\left(x+y\right)+4\left(x+y\right)\\ =\left(x+y\right)\left(z+4\right)\\ c,x^2-x-y^2+y\\ =\left(x-y\right)\left(x+y\right)-\left(x-y\right)\\ =\left(x-y\right)\left(x+y-1\right)\\ d,x^2+2x+2z-z^2\\ =\left(x-z\right)\left(x+z\right)+2\left(x+z\right)\\ =\left(x+z\right)\left(x-z+2\right)\)
Bài 1B:
\(a,x^2+2xy+x+2y\\ =x\left(x+2y\right)+\left(x+2y\right)\\ =\left(x+2y\right)\left(x+1\right)\\ b,2xy+yz+2x+z\\ =y\left(2x+z\right)+\left(2x+z\right)\\ =\left(y+1\right)\left(2x+z\right)\\ c,y^2-2y-z^2-2z\\ =\left(y-z\right)\left(y+z\right)-2\left(y+z\right)\\ =\left(y+z\right)\left(y-z-2\right)\\ d,x^3-x-y+y^3\\ =\left(x+y\right)\left(x^2-xy+y^2\right)-\left(x+y\right)\\ =\left(x+y\right)\left(x^2-xy+y^2-1\right)\)
1B
a)
\(=x\left(x+2y\right)+\left(x+2y\right)\\ =\left(x+1\right)\left(x+2y\right)\)
b)
\(=y\left(2x+z\right)+\left(2x+z\right)\\ =\left(y+1\right)\left(2x+z\right)\)
c)
\(=\left(y^2-z^2\right)-\left(2y+2z\right)\\ =\left(y-z\right)\left(y+z\right)-2\left(y+z\right)\\ =\left(y+z\right)\left(y-z-2\right)\)
d)
\(=\left(x^3+y^3\right)-\left(x+y\right)\\ =\left(x+y\right)\left(x^2-xy+y^2\right)-\left(x+y\right)\\ =\left(x+y\right)\left(x^2-xy+y^2-1\right)\)