Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Lời giải:

$x^3+y^3+3xy(x+y)=x^3+3x^2y+3xy^2+y^3=(x+y)^3$

P.s: Lần sau bạn chú ý ghi đầy đủ yêu cầu đề nhé.

a: \(16-x^2=4^2-x^2=\left(4-x\right)\left(4+x\right)\)

b: \(x^2-8x+16\)

\(=x^2-2\cdot x\cdot4+4^2\)

\(=\left(x-4\right)^2\)

c: \(x^2-2x+1-y^2\)

\(=\left(x^2-2x+1\right)-y^2\)

\(=\left(x-1\right)^2-y^2\)

\(=\left(x-1-y\right)\left(x-1+y\right)\)

d: \(x^2+2xy+y^2-1\)

\(=\left(x^2+2xy+y^2\right)-1\)

\(=\left(x+y\right)^2-1\)

\(=\left(x+y+1\right)\left(x+y-1\right)\)

a: \(x^3-4x=x\cdot x^2-x\cdot4\)

\(=x\left(x^2-4\right)\)

\(=x\left(x-2\right)\left(x+2\right)\)

b: \(xy-3x\)

\(=x\cdot y-x\cdot3\)

=x(y-3)

c: \(x^2+4xy+4y^2-25\)

\(=\left(x^2+4xy+4y^2\right)-25\)

\(=\left(x+2y\right)^2-5^2\)

\(=\left(x+2y+5\right)\left(x+2y-5\right)\)

d: \(x^2+25-10x\)

\(=x^2-2\cdot x\cdot5+5^2\)

\(=\left(x-5\right)^2\)

e: \(x^3-8y^3\)

\(=x^3-\left(2y\right)^3\)

\(=\left(x-2y\right)\left(x^2+2xy+4y^2\right)\)

a: \(a^3-3a+3b-b^3\)

\(=\left(a^3-b^3\right)-\left(3a-3b\right)\)

\(=\left(a-b\right)\left(a^2+ab+b^2\right)-3\left(a-b\right)\)

\(=\left(a-b\right)\left(a^2+ab+b^2-3\right)\)

b: \(a^2+6ab+9b^2-1\)

\(=\left(a^2+6ab+9b^2\right)-1\)

\(=\left(a+3b\right)^2-1\)

\(=\left(a+3b-1\right)\left(a+3b+1\right)\)

c: \(4x^2-25+\left(2x+7\right)\left(5-2x\right)\)

\(=\left(4x^2-25\right)-\left(2x+7\right)\left(2x-5\right)\)

\(=\left(2x-5\right)\left(2x+5\right)-\left(2x+7\right)\left(2x-5\right)\)

\(=\left(2x-5\right)\left(2x+5-2x-7\right)\)

\(=-2\cdot\left(2x-5\right)\)

d: \(x^2+2x-15\)

\(=x^2+5x-3x-15\)

\(=\left(x^2+5x\right)-\left(3x+15\right)\)

\(=x\left(x+5\right)-3\left(x+5\right)\)

\(=\left(x+5\right)\left(x-3\right)\)

e: \(2x^3+3x^2-5x\)

\(=x\left(2x^2+3x-5\right)\)

\(=x\left(2x^2+5x-2x-5\right)\)

\(=x\left[x\left(2x+5\right)-\left(2x+5\right)\right]\)

\(=x\left(2x+5\right)\left(x-1\right)\)

f: \(2x^3-4x^2+2x-4\)

\(=2\left(x^3-2x^2+x-2\right)\)

\(=2\left[x^2\left(x-2\right)+\left(x-2\right)\right]\)

\(=2\left(x-2\right)\left(x^2+1\right)\)

g: \(x^3-4x^2-8x+8\)

\(=\left(x^3+8\right)-\left(4x^2+8x\right)\)

\(=\left(x+2\right)\left(x^2-2x+4\right)-4x\left(x+2\right)\)

\(=\left(x+2\right)\left(x^2-2x+4-4x\right)\)

\(=\left(x+2\right)\left(x^2-6x+4\right)\)

h: \(x^2-7xy+10y^2\)

\(=x^2-2xy-5xy+10y^2\)

\(=\left(x^2-2xy\right)-\left(5xy-10y^2\right)\)

\(=x\left(x-2y\right)-5y\left(x-2y\right)\)

\(=\left(x-2y\right)\left(x-5y\right)\)

Câu 17:

Xét ΔADC có OE//DC

nên \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)

Xét ΔBDC có OH//DC

nên \(\dfrac{OH}{DC}=\dfrac{BO}{BD}\left(2\right)\)

Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)

\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)

Do đó: ΔOAB đồng dạng với ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)

=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)

=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)

=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)

=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)

=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\dfrac{OE}{DC}=\dfrac{OH}{DC}\)

=>OE=OH

Câu 15:

a: \(3x\left(x-1\right)+x-1=0\)

=>\(3x\left(x-1\right)+\left(x-1\right)=0\)

=>\(\left(x-1\right)\left(3x+1\right)=0\)

=>\(\left[{}\begin{matrix}x-1=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)

b: \(x^2-6x=0\)

=>\(x\cdot x-x\cdot6=0\)

=>x(x-6)=0

=>\(\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)

a: \(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)

\(=\left(x^2+x\right)^2+2\left(x^2+x\right)+\left(x^2+x\right)+2-12\)

\(=\left(x^2+x\right)^2+3\left(x^2+x\right)-10\)

\(=\left(x^2+x\right)^2+5\left(x^2+x\right)-2\left(x^2+x\right)-10\)

\(=\left(x^2+x\right)\left(x^2+x+5\right)-2\left(x^2+x+5\right)\)

\(=\left(x^2+x+5\right)\left(x^2+x-2\right)\)

\(=\left(x^2+x+5\right)\left(x^2+2x-x-2\right)\)

\(=\left(x^2+x+5\right)\left[x\left(x+2\right)-\left(x+2\right)\right]\)

\(=\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)

b: \(\left(x^2+2x\right)^2+9x^2+18x+20\)

\(=\left(x^2+2x\right)^2+9\left(x^2+2x\right)+20\)

\(=\left(x^2+2x\right)^2+4\left(x^2+2x\right)+5\left(x^2+2x\right)+20\)

\(=\left(x^2+2x\right)\left(x^2+2x+4\right)+5\left(x^2+2x+4\right)\)

\(=\left(x^2+2x+4\right)\left(x^2+2x+5\right)\)

c: \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)

\(=\left(x+2\right)\left(x+8\right)\left(x+4\right)\left(x+6\right)+16\)

\(=\left(x^2+8x+2x+16\right)\left(x^2+6x+4x+24\right)+16\)

\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)

\(=\left(x^2+10x\right)^2+24\left(x^2+10x\right)+16\left(x^2+10x\right)+384+16\)

\(=\left(x^2+10x\right)^2+40\left(x^2+10x\right)+400\)

\(=\left(x^2+10x+20\right)^2\)

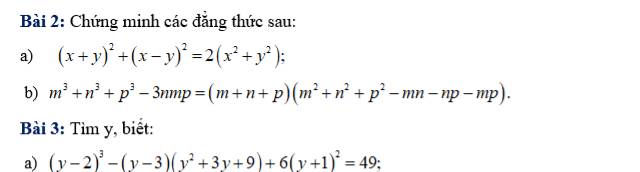
Bài 3:

a: \(\left(y-2\right)^3-\left(y-3\right)\left(y^2+3y+9\right)+6\left(y+1\right)^2=49\)

=>\(y^3-6y^2+12y-8-\left(y^3-27\right)+6\left(y^2+2y+1\right)=49\)

=>\(y^3-6y^2+12y-8-y^3+27+6y^2+12y+6=49\)

=>\(24y+25=49\)

=>24y=24

=>y=1

Bài 2:

a: \(\left(x+y\right)^2+\left(x-y\right)^2\)

\(=x^2+2xy+y^2+x^2-2xy+y^2\)

\(=2x^2+2y^2=2\left(x^2+y^2\right)\)

b: \(m^3+n^3+p^3-3mnp\)

\(=\left(m+n\right)^3-3mn\left(m+n\right)+p^3-3mnp\)

\(=\left(m+n\right)^3+p^3-3mn\left(m+n\right)-3mpn\)

\(=\left(m+n+p\right)\left[\left(m+n\right)^2-p\left(m+n\right)+p^2\right]-3mn\left(m+n+p\right)\)

\(=\left(m+n+p\right)\left(m^2+2mn+n^2-pm-pn+p^2-3mn\right)\)

\(=\left(m+n+p\right)\left(m^2+n^2+p^2-mn-mp-np\right)\)

Bài 2

a) \(VT=\left(x+y\right)^2+\left(x-y\right)^2\)

\(=x^2+2xy+y^2+x^2-2xy+y^2\)

\(=\left(x^2+x^2\right)+\left(2xy-2xy\right)+\left(y^2+y^2\right)\)

\(=2x^2+2y^2\)

\(=2\left(x^2+y^2\right)\)

\(=VP\)

Vậy \(\left(x+y\right)^2+\left(x-y^2\right)=2\left(x^2+y^2\right)\)

b) \(VP=\left(m+n+p\right)\left(m^2+n^2+p^2-mn-np-mp\right)\)

\(=m^3+mn^2+mp^2-m^2n-mnp-m^2p+m^2n+n^3+np^2-mn^2-n^2p-mnp+m^2p+n^2p+p^3-mnp-np^2-mp^2\)

\(=m^3+n^3+p^3+\left(mn^2-mn^2\right)+\left(mp^2-mp^2\right)+\left(-m^2n+m^2n\right)+\left(-mnp-mnp-mnp\right)+\left(n^2p-n^2p\right)+\left(np^2-np^2\right)+\left(m^2p-m^2p\right)\)

\(=m^3+n^3+p^3-3mnp\)

\(=VP\)

Vậy \(m^3+n^3+p^3-3mnp=\left(m+n+p\right)\left(m^2+n^2+p^2-mn-np-mp\right)\)

Bài 3

a) \(\left(y-2\right)^3-\left(y-3\right)\left(y^2+3y+9\right)+6\left(y+1\right)^2=49\)

\(y^3-6y^2+12y-8-y^3+27+6y^2+12y+6=49\)

\(\left(y^3-y^3\right)+\left(-6y^2+6y^2\right)+\left(12y+12y\right)+25=49\)

\(24y=49-25\)

\(24y=24\)

\(y=\dfrac{24}{24}\)

\(y=1\)

\(\left(a+b+c\right)^3=a^3+b^3+c^3\)

=>\(a^3+b^3+c^3+3\left(a+b\right)\left(a+c\right)\left(b+c\right)=a^3+b^3+c^3\)

=>\(3\left(a+b\right)\left(a+c\right)\left(b+c\right)=0\)

=>\(\left(a+b\right)\left(a+c\right)\left(b+c\right)=0\)

\(T=\left(a+b\right)\cdot\left(b+c\right)^2\cdot\left(c+a\right)^2\)

\(=\left(a+b\right)\left(a+c\right)\left(b+c\right)\cdot\left(b+c\right)\left(a+c\right)\)

\(=0\cdot\left(b+c\right)\left(a+c\right)\)

=0

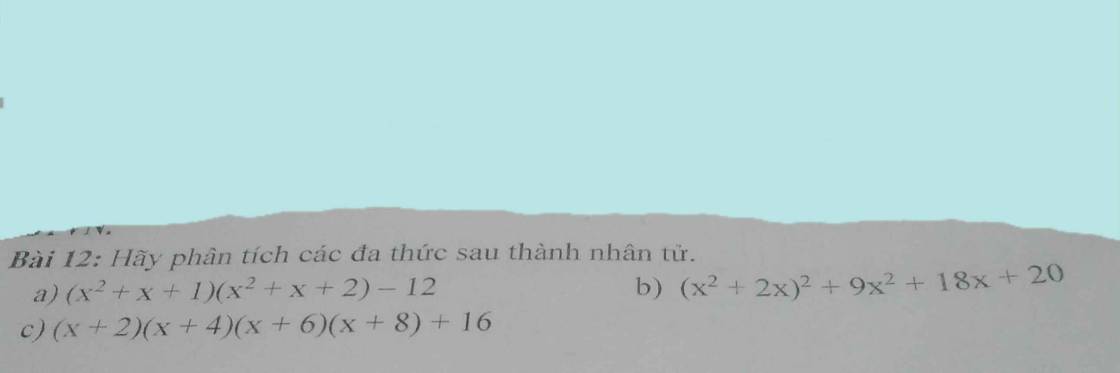
a) \(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)

Đặt: \(x^2+x+1=y\), khi đó biểu thức trở thành:

\(y\left(y+1\right)-12\)

\(=y^2+y-12\)

\(=y^2-3y+4y-12\)

\(=y\left(y-3\right)+4\left(y-3\right)\)

\(=\left(y-3\right)\left(y+4\right)\)

\(=\left(x^2+x+1-3\right)\left(x^2+x+1+4\right)\)

\(=\left(x^2+x-2\right)\left(x^2+x+5\right)\)

\(=\left(x^2-x+2x-2\right)\left(x^2+x+5\right)\)

\(=\left[x\left(x-1\right)+2\left(x-1\right)\right]\left(x^2+x+5\right)\)

\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+5\right)\)

b) \(\left(x^2+2x\right)^2+9x^2+18x+20\)

\(=\left(x^2+2x\right)^2+9\left(x^2+2x\right)+20\)

Đặt: \(x^2+2x=a\), khi đó biểu thức trở thành:

\(a^2+9a+20\)

\(=a^2+4a+5a+20\)

\(=a\left(a+4\right)+5\left(a+4\right)\)

\(=\left(a+4\right)\left(a+5\right)\)

\(=\left(x^2+2x+4\right)\left(x^2+2x+5\right)\)

c) \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)

\(=\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]+16\)

\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)

Đặt: \(x^2+10x+20=y\), khi đó biểu thức trở thành:

\(\left(y-4\right)\left(y+4\right)+16\)

\(=y^2-16+16\)

\(=y^2\)

\(=\left(x^2+10x+20\right)^2\)

$\text{#}Toru$

$(x^2-2)^2+4(x-1)^2-4(x^2-2)(x-1)=0$

$\Leftrightarrow(x^2-2)^2-4(x^2-2)(x-1)+4(x-1)^2=0$

$\Leftrightarrow(x^2-2)^2-2\cdot(x^2-2)\cdot2(x-1)+[2(x-1)]^2=0$

$\Leftrightarrow[(x^2-2)-2(x-1)]^2=0$

$\Leftrightarrow(x^2-2-2x+2)^2=0$

$\Leftrightarrow(x^2-2x)^2=0$

$\Leftrightarrow x^2-2x=0$

$\Leftrightarrow x(x-2)=0$

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

Vậy: $x\in\{0;2\}$.