Bài 12: Chia đa thức một biến đã sắp xếp
Nội dung lý thuyết
Các phiên bản khác1. Phép chia hết
Xét bài toán: Thực hiện phép chia đa thức \(2x^4-13x^3+15x^2+11x-3\) cho đa thức \(x^2-4x-3\).
Ta thực hiện theo các bước:
- Sắp xếp đa thức bị chia và đa thức chia theo đúng thứ tự giảm dần của lũy thừa.
Ở đây, các đa thức đã được sắp xếp theo thứ tự trên.
- Đặt phép chia.

Chia hạng tử bậc cao nhất của đa thức bị chia cho hạng tử bậc cao nhất của đa thức chia, viết kết quả vào dòng thương:
\(2x^4:x^2=2x^2\)
Nhân \(2x^2\) với đa thức chia \(x^2-4x-3\), viết kết quả theo quy tắc các lũy thừa giống nhau thì thẳng cột. Đến đây, lấy đa thức bị chia trừ đi tích vừa nhận được:
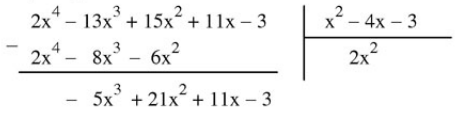
Hiệu \(-5x^3+21x^2+11x-3\) được gọi là dư thứ nhất.
- Bây giờ, ta thực hiện phép chia dư thứ nhất cho đa thức chia.
Chia hạng tử bậc cao nhất của dư thứ nhất cho hạng tử bậc cao nhất của đa thức chia, viết kết quả vào dòng thương:
\(-5x^3:x^2=-5x\)
Lấy dư thứ nhất trừ đi tích của \(-5x\) và đa thức chia, ta được dư thứ hai:
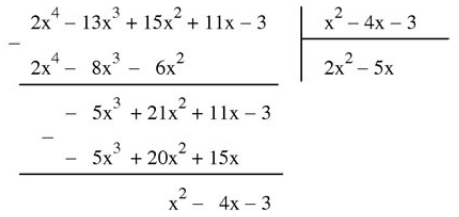
Tiếp tục thực hiện tương tự như trên, ta có:
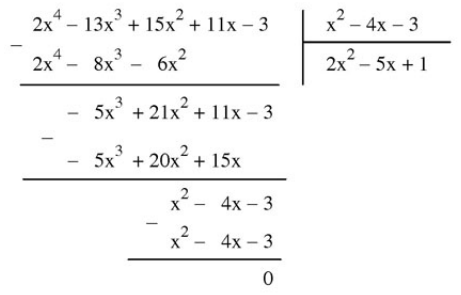
- Dư cuối cùng bằng 0, ta kết thúc phép toán và được thương là \(2x^2-5x+1\). Khi đó, ta viết:
\(\left(2x^4-13x^3+15x^2+11x-3\right):\left(x^2-4x-3\right)=2x^2-5x+1.\)
Các phép chia có số dư bằng 0 được gọi là các phép chia hết.
2. Phép chia có dư
Xét bài toán: Thực hiện phép chia đa thức \(5x^3-3x^2+7\) cho đa thức \(x^2+1\).
Thực hiện tương tự các bước làm trong ví dụ phía trên, ta có:

Đến đây, ta thấy: Bậc của đa thức dư \(-5x+10\) bằng 1, nhỏ hơn bậc của đa thức chia \(x^2+1\). Do đó, phép chia không thể thực hiện tiếp được nữa.
Trong trường hợp này, ta nói đây là phép chia có dư, đa thức \(-5x+10\) được gọi là dư. Khi đó, ta có thể viết:
\(5x^3-3x^2+7=\left(x^2+1\right)\left(5x-3\right)+\left(-5x+10\right).\)
Chú ý: Với hai đa thức tùy ý \(A\) và \(B\) của cùng một biến (\(B\ne0\)), tồn tại duy nhất một cặp đa thức \(Q\) và \(R\) sao cho \(A=B.Q+R\), trong đó \(R=0\) hoặc bậc của \(R\) nhỏ hơn bậc của \(B\). Khi đó, \(R\) được gọi là dư trong phép chia \(A\) cho \(B\).
- Nếu \(R=0\): phép chia \(A\) cho \(B\) là phép chia hết.
- Nếu \(R\ne0\): phép chia \(A\) cho \(B\) là phép chia có dư.
Nhận xét:
- Trước khi thực hiện phép chia, cần sắp xếp các hạng tử của cả đa thức chia và đa thức bị chia theo đúng thứ tự giảm dần của lũy thừa.
- Khi đặt phép tính, cần đặt các hạng tử cùng lũy thừa thẳng cột với nhau.
- Cẩn thận khi làm việc với các dấu cộng, trừ của phép toán.
@543261@@543445@