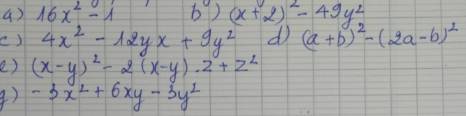a) \(16x^2-1\)
\(=\left(4x\right)^2-1^2\)
\(=\left(4x-1\right)\left(4x+1\right)\)
b) \(\left(x+2\right)^2-49y^2\)
\(=\left(x+2\right)^{^2}-\left(7y\right)^2\)
\(=\left[\left(x+2\right)-7y\right]\left[\left(x+2\right)+7y\right]\)
\(=\left(x+2-7y\right)\left(x+2+7y\right)\)
c) \(4x^2-12xy+9y^2\)
\(=\left(2x\right)^2-2\cdot2x\cdot3y+\left(3y\right)^2\)
\(=\left(2x-3y\right)^2\)
d) \(\left(a+b\right)^2-\left(2a-b\right)^2\)
\(=\left[\left(a+b\right)+\left(2a-b\right)\right]\left[\left(a+b\right)-\left(2a-b\right)\right]\)
\(=\left(a+b+2a-b\right)\left(a+b-2a+b\right)\)
\(=3a\cdot\left(2b-a\right)\)
e) \(\left(x-y\right)^2-2\left(x-y\right)z+z^2\)
\(=\left[\left(x-y\right)-z\right]^2\)
\(=\left(x-y-z\right)^2\)
g) \(-3x^2+6xy-3y^2\)
\(=-\left(3x^2-6xy+3y^2\right)\)
\(=-3\left(x^2-2xy+y^2\right)\)
\(=-3\left(x-y\right)^2\)
a: 16x^2-1=(4x)^2-1=(4x-1)(4x+1)
b: (x+2)^2-49y^2
=(x+2)^2-(7y)^2
=(x+2+7y)(x+2-7y)
c: 4x^2-12xy+9y^2=(2x-3y)^2
d: (a+b)^2-(2a-b)^2
=(a+b+2a-b)(a+b-2a+b)
=(2b-a)*3a
g: =-3(x^2-2xy+y^2)
=-3(x-y)^2