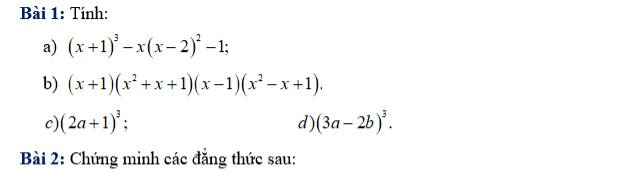
Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

\(a,\left(x+1\right)^3-x\left(x-2\right)^2-1\\ =\left(x^3+3x^2+3x+1\right)-x\left(x^2-4x+4\right)-1\\ =x^3-x^3+3x^2+4x^2+3x-4x+1-1\\ =7x^2-x\\ ---\\ b,\left(x+1\right)\left(x^2+x+1\right)\left(x-1\right)\left(x^2-x+1\right)\\ =\left[\left(x+1\right)\left(x^2-x+1\right)\right].\left[\left(x-1\right)\left(x^2+x+1\right)\right]=\left(x^3+1\right)\left(x^3-1\right)=x^6-1\\ ---\\ c,\left(2x+1\right)^3=\left(2a\right)^3+3.\left(2a\right)^2.1+3.2a.1^2+1^3=8a^3+12a^2+6a+1\\ d,\left(3a-2b\right)^3=\left(3a\right)^3-3.\left(3a\right)^2.2b+3.3a.\left(2b\right)^2-\left(2b\right)^3\\ =27a^3-54a^2b+36ab^2-8b^3\)

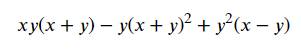
\(xy\left(x+y\right)-y\left(x+y\right)^2+y^2\left(x-y\right)\)

\(=\left(x+y\right)\left(xy-xy-y^2\right)+y^2\left(x-y\right)\)

\(=-y^2\left(x+y\right)+y^2\left(x-y\right)\)

\(=y^2\left(-x-y+x-y\right)\)

\(=-2y^3\)

a: \(x^2-9-x^2\left(x^2-9\right)\)

\(=\left(x^2-9\right)-x^2\left(x^2-9\right)\)

\(=\left(x^2-9\right)\left(1-x^2\right)\)

\(=\left(1-x\right)\left(1+x\right)\left(x-3\right)\left(x+3\right)\)

b: \(x^2\left(x-y\right)+y^2\left(y-x\right)\)

\(=x^2\left(x-y\right)-y^2\left(x-y\right)\)

\(=\left(x-y\right)\left(x^2-y^2\right)\)

\(=\left(x-y\right)\left(x-y\right)\left(x+y\right)=\left(x-y\right)^2\cdot\left(x+y\right)\)

c: \(x^3+27+\left(x+3\right)\left(x-9\right)\)

\(=\left(x+3\right)\left(x^2-3x+9\right)+\left(x+3\right)\left(x-9\right)\)

\(=\left(x+3\right)\left(x^2-3x+9+x-9\right)\)

\(=\left(x+3\right)\left(x^2-2x\right)=x\left(x-2\right)\left(x+3\right)\)

d: \(x^2+5x+6\)

\(=x^2+2x+3x+6\)

\(=x\left(x+2\right)+3\left(x+2\right)=\left(x+2\right)\left(x+3\right)\)

e: \(3x^2-4x-4\)

\(=3x^2-6x+2x-4\)

\(=3x\left(x-2\right)+2\left(x-2\right)\)

\(=\left(x-2\right)\left(3x+2\right)\)

g: \(x^4+64y^4\)

\(=x^4+16x^2y^2+64y^4-16x^2y^2\)

\(=\left(x^2+8y^2\right)^2-\left(4xy\right)^2\)

\(=\left(x^2+8y^2-4xy\right)\left(x^2+8y^2+4xy\right)\)

h: \(a^2+b^2+2a-2b-2ab\)

\(=a^2-2ab+b^2+2a-2b\)

\(=\left(a-b\right)^2+2\left(a-b\right)=\left(a-b\right)\left(a-b+2\right)\)

i: \(\left(x+1\right)^2-2\left(x+1\right)\left(y-3\right)+\left(y-3\right)^2\)

\(=\left(x+1-y+3\right)^2\)

\(=\left(x-y+4\right)^2\)

k: \(x^2\left(x+1\right)-2x\left(x+1\right)+\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2-2x+1\right)\)

\(=\left(x+1\right)\left(x-1\right)^2\)

a: Xét tứ giác BHCD có

M là trung điểm chung của BC và HD

=>BHCD là hình bình hành

b: BHCD là hình bình hành

=>BH//CD và BD//CH

BH//CD

BH\(\perp\)CA

Do đó: CD\(\perp\)CA

=>ΔCDA vuông tại C

BD//CH

AB\(\perp\)CH

Do đó: BA\(\perp\)BD

=>ΔBAD vuông tại B

c: ΔBAD vuông tại B có BI là đường trung tuyến

nên IA=IB=ID

ΔCAD vuông tại C có CI là đường trung tuyến

nên CI=AI=DI

=>IA=IB=IC=ID

`#3107.101107`

`x(y - 1) + 3(y - 1)`

`= (x + 3)(y - 1)`

x(y-1)+3(y-1)

=(y-1)(x+3)

Giải thích: đặt y-1 ra làm chung .... đa thức còn x+3

`#3107.101107`

`(x^2x^2 - 8)^2 - 1`

`= (x^4 - 8)^2 - 1^2`

`= (x^4 - 8 - 1)(x^4 - 8 + 1)`

`= (x^4 - 9)(x^4 - 7)`

`= [ (x^2)^2 - 3^2](x^4 - 7)`

`= (x^2 - 3)(x^2 + 3)(x^4 - 7)`

\(x^2-7x-8\\=x^2+x-8x-8\\=x(x+1)-8(x+1)\\=(x+1)(x-8)\)

\(=y\left(4x^2-4xy+y^2-49\right)\)

\(=y\left[\left(2x-y\right)^2-49\right]\)

\(=y\left(2x-y-7\right)\left(2x-y+7\right)\)

Biểu thức này không phân tích được thành nhân tử nhé. Bạn xem xem có viết sai đề không.

`x^2-4=2(x+2)^2`.

`<=> x^2-4=2x^2+8x+8`.

`<=> x^2+8x+12=0`

`<=> (x+6)(x+2)=0`

`<=> x+6=0` hoặc `x+2=0`

`<=> x=-6` hoặc `x=-2`.