Cho tam giác cân ABC có AB = BC. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. Chứng minh MN // AC
Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử
Do CN là phân giác, áp dụng định lý phân giác:
\(\dfrac{BN}{AN}=\dfrac{BC}{AC}\)
Do AM là phân giác, áp dụng định lý phân giác:
\(\dfrac{BM}{CM}=\dfrac{AB}{AC}\)
Mà \(AB=BC\Rightarrow\dfrac{BC}{AC}=\dfrac{AB}{AC}\)
\(\Rightarrow\dfrac{BN}{AN}=\dfrac{BM}{CM}\Rightarrow MN||AC\) (định lý Talet đảo)
Đúng 0
Bình luận (0)
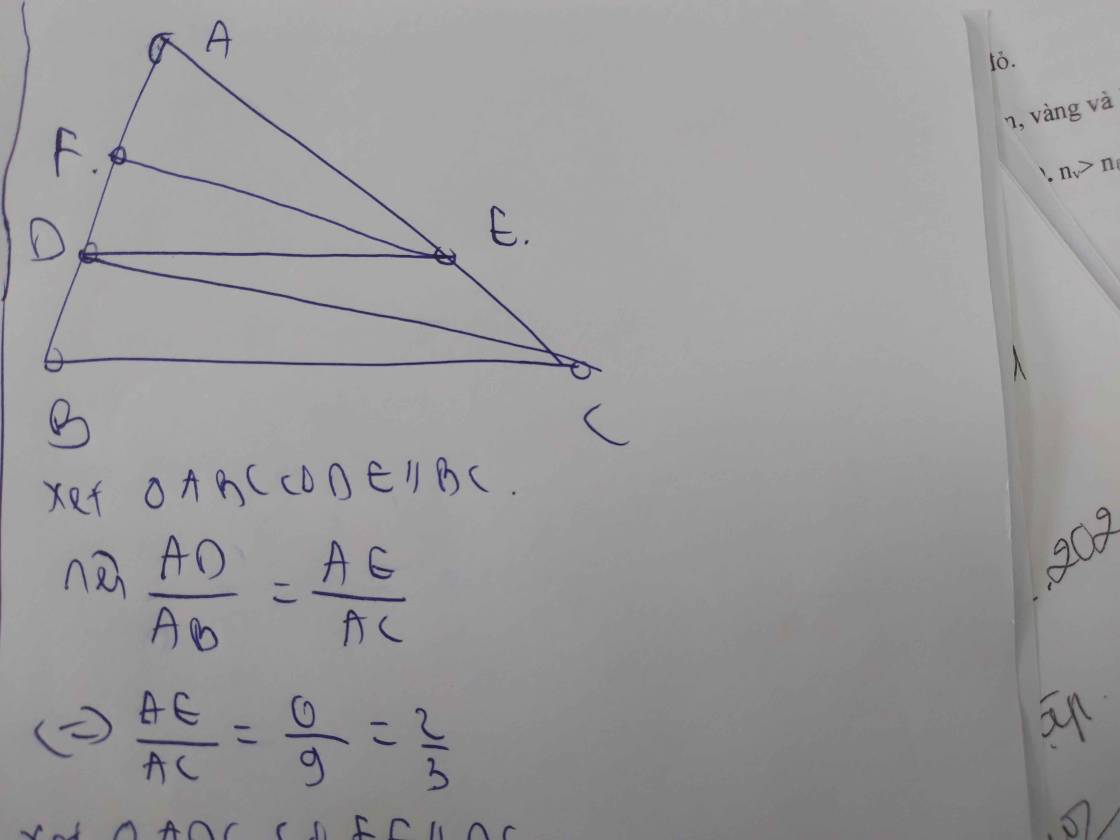
Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E Є AC), kẻ EF song song với CD (F Є AB). Tính độ dài AF.
Cho a+b=1, tính giá trị biểu thức sau: M=a³+b³+3ab(a²+b²)+6a²b²(a+b) Cứu mình với
\(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ba\left[\left(a+b\right)^2-2ab\right]+6a^2b^2\)
\(=1-3ab+3ab\left(1-2ab\right)+6a^2b^2\)
\(=1-3ab+3ab-6a^2b^2+6a^2b^2\)
=1
Đúng 0
Bình luận (0)
Phân tích đa thức thành Nhân tử:4xy-x²+9-4y²
4xy - x² + 9 - 4y²
= -(x² - 4xy + 4y² - 9)
= -[(x² - 4xy + 4y²) - 3²]
= -[(x - 2y)² - 3²]
= -(x - 2y - 3)(x - 2y + 3)
Đúng 1
Bình luận (0)
cho a+b+c=6, a2+b2+c2=12
Tính giá trị A=(a-3)2020+(b-3)2020+(c-3)2020
Lời giải:
Ta có:
$2(ab+bc+ac)=(a+b+c)^2-(a^2+b^2+c^2)=6^2-12=24=2(a^2+b^2+c^2)$
$\Rightarrow 2(a^2+b^2+c^2)-2(ab+bc+ac)=0$
$\Leftrightarrow (a^2+b^2-2ab)+(b^2+c^2-2bc)+(c^2+a^2-2ac)=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
$\Rightarrow a-b=b-c=c-a=0$
$\Rightarrow a=b=c$. Mà $a+b+c=6$ nên $a=b=c=2$
Khi đó:
$A=(2-3)^{2020}+(2-3)^{2020}+(2-3)^{2020}=1+1+1=3$
Đúng 2
Bình luận (0)
4x2 – y2 + 4y – 4
\(4x^2-y^2+4y-4\\=4x^2-(y^2-4y+4)\\=4x^2-(y^2-2\cdot y\cdot2+2^2)\\=(2x)^2-(y-2)^2\\=[2x-(y-2)][2x+(y-2)]\\=(2x-y+2)(2x+y-2)\)
Đúng 2
Bình luận (0)
a: \(25x^2\left(x-3y\right)-15\left(3y-x\right)\)
\(=25x^2\left(x-3y\right)+15\left(x-3y\right)\)
\(=\left(x-3y\right)\left(25x^2+15\right)\)
\(=5\left(5x^2+3\right)\left(x-3y\right)\)
b: \(x^4-5x^2+4\)
\(=x^4-x^2-4x^2+4\)
\(=\left(x^4-x^2\right)-\left(4x^2-4\right)\)
\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)\)
\(=\left(x^2-1\right)\left(x^2-4\right)\)
\(=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức
a,x3 + x2 + x+1
b. ax+ay .3x - 3y
c.x2 + ab + ax +bx
d.xy + 1+x+y
a: \(x^3+x^2+x+1\)
\(=\left(x^3+x^2\right)+\left(x+1\right)\)
\(=x^2\left(x+1\right)+\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+1\right)\)
b: Sửa đề: \(ax+ay-3x-3y\)
\(=\left(ax+ay\right)-\left(3x+3y\right)\)
\(=a\left(x+y\right)-3\left(x+y\right)\)
\(=\left(x+y\right)\left(a-3\right)\)
c: \(x^2+ab+ax+bx\)
\(=\left(x^2+ax\right)+\left(ab+bx\right)\)
\(=x\left(x+a\right)+b\left(a+x\right)\)
\(=\left(x+a\right)\left(x+b\right)\)
d: \(xy+1+x+y\)
\(=\left(xy+x\right)+\left(y+1\right)\)
\(=x\left(y+1\right)+\left(y+1\right)\)
\(=\left(x+1\right)\left(y+1\right)\)
Đúng 3
Bình luận (0)
a.
\(x^3+x^2+x+1\\ =x^2\left(x+1\right)+\left(x+1\right)\\ =\left(x^2+1\right)\left(x+1\right)\)
b.
\(ax+ay-3x-3y\\ =ax+ay-\left(3x+3y\right)\\ =a\left(x+y\right)-3\left(x+y\right)\\ =\left(a-3\right)\left(x+y\right)\)
c.
\(x^2+ab+ax+bx\\ =\left(x^2+ax\right)+\left(ab+bx\right)\\ =x\left(x+a\right)+b\left(a+x\right)\\ =\left(x+a\right)\left(x+b\right)\)
d.
\(xy+1+x+y\\ =\left(xy+x\right)+\left(1+y\right)\\ =x\left(y+1\right)+\left(y+1\right)\\ =\left(x+1\right)\left(y+1\right)\)
Đúng 2
Bình luận (1)
b.
ax+ay−3x−3y=ax+ay−(3x+3y)=a(x+y)−3(x+y)=(a−3)(x+y)
d.
xy+1+x+y=(xy+x)+(1+y)=x(y+1)+(y+1)=(x+1)(y+1)
Đúng 0
Bình luận (0)
\(13,x^2-x-3x+3\\ =x\left(x-1\right)-3\left(x-1\right)\\ =\left(x-3\right)\left(x-1\right)\\ ---\\ 16,x^3-3x^2-4x+12\\ =x^2\left(x-3\right)-4\left(x-3\right)\\ =\left(x-3\right)\left(x^2-4\right)\\ =\left(x-3\right)\left(x-2\right)\left(x+2\right)\\ ---\\ 15,x^2-2x-3x+6\\ =x\left(x-2\right)-3\left(x-2\right)\\ =\left(x-3\right)\left(x-2\right)\\ ---\\ 14,x^2+x+3x+3\\ =x\left(x+1\right)+3\left(x+1\right)\\ =\left(x+3\right)\left(x+1\right)\\ ---\\ 17,45+x^3-5x^2-9x\\ =x^2\left(x-5\right)-9\left(x-5\right)\\ =\left(x^2-9\right)\left(x-5\right)\\ =\left(x-3\right)\left(x+3\right)\left(x-5\right)\\ ---\\ 18,x^5+x^4+x+1\\ =x^4\left(x+1\right)+\left(x+1\right)\\ =\left(x^4+1\right)\left(x+1\right)\)
Đúng 3
Bình luận (0)
\(26,3x^2-3xy-5x+5y\\ =3x\left(x-y\right)+5\left(x-y\right)\\ =\left(3x+5\right)\left(x-y\right)\\ ---\\ 27,xz+yz-5x-5y\\ =z\left(x+y\right)-5\left(x+y\right)\\ =\left(z-5\right)\left(x+y\right)\\ ----\\ 21,x^5+x^4+x+1\\ =x^4\left(x+1\right)+\left(x+1\right)\\ =\left(x^4+1\right)\left(x+1\right)\\ ---\\ 24,ax+ay+bx+by\\ =a\left(x+y\right)+b\left(x+y\right)\\ =\left(a+b\right)\left(x+y\right)\\ ---\\ 27,5a^2-5ax-7a+7x\\ =5a\left(a-x\right)-7\left(a-x\right)\\ =\left(5a-7\right)\left(a-x\right)\\ ---\\ 30,3x^2-3xy-5x+5y\\ =3x\left(x-y\right)-5\left(x-y\right)\\ =\left(3x-5\right)\left(x-y\right)\)
Đúng 2
Bình luận (0)
\(19,x^4-9x^3+x^2-9x\\ =x^3\left(x-9\right)+x\left(x-9\right)\\ =\left(x^3+x\right)\left(x-9\right)\\ =x\left(x^2+1\right)\left(x-9\right)\\ ---\\ 22,x^3+x^2+x+1\\ =x^2\left(x+1\right)+\left(x+1\right)\\ =\left(x^2+1\right)\left(x+1\right)\\ ---\\ 25,x^2-xy+x-y\\ =x\left(x-y\right)+\left(x-y\right)\\ =\left(x-y\right)\left(x+1\right)\\ ---\\ 20,x^3+x^2+x+1\\ =x^2\left(x+1\right)+\left(x+1\right)\\ =\left(x+1\right)\left(x^2+1\right)\\ ---\\ 28,x^2-xy+x-y\\ =x\left(x-y\right)+\left(x-y\right)\\ =\left(x+1\right)\left(x-y\right)\\ ---\\ 23,x^3+7x^2-4x-28\\ =x^2\left(x+7\right)-4\left(x+7\right)\\ =\left(x^2-4\right)\left(x+7\right)\\ =\left(x-2\right)\left(x+2\right)\left(x+7\right)\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Chi tiết nhất ạ thanks mn nhiều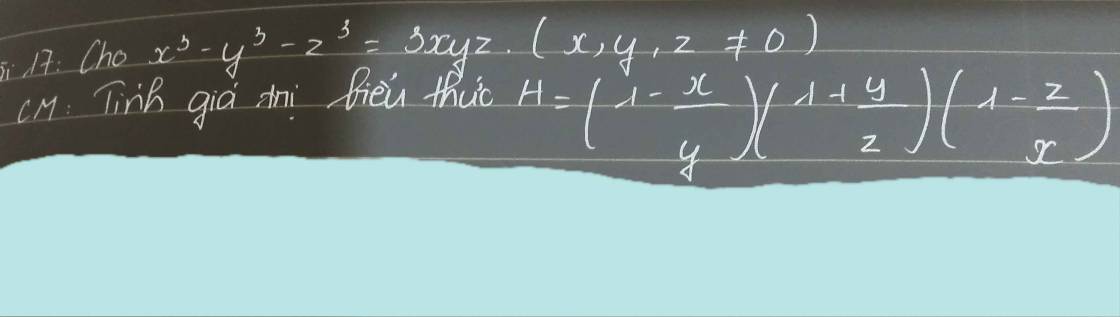
\(x^3-y^3-z^3=3xyz\)
=>\(\left(x-y\right)^3-z^3+3xy\left(x-y\right)-3xyz=0\)
=>\(\left(x-y-z\right)\left[\left(x-y\right)^2+z\left(x-y\right)+z^2\right]+3xy\left(x-y-z\right)=0\)
=>\(\left(x-y-z\right)\left[x^2-2xy+y^2+xz-zy+z^2+3xy\right]=0\)
=>\(\left(x-y-z\right)\left(x^2+y^2+z^2+xy+xz-yz\right)=0\)
=>\(\left(x-y-z\right)\left(2x^2+2y^2+2z^2+2xy+2xz-2yz\right)=0\)
=>\(\left(x-y-z\right)\left[\left(x^2+2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(x^2+2xz+z^2\right)\right]=0\)
=>\(\left(x-y-z\right)\left[\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2\right]=0\)
=>\(\left[{}\begin{matrix}x-y-z=0\\\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=y+z\\y=z=-x\end{matrix}\right.\)
\(H=\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1-\dfrac{z}{x}\right)\)
\(=\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}\cdot\dfrac{x-z}{x}\)
TH1: x=y+z
=>\(H=\dfrac{y-x}{y}\cdot\dfrac{x}{z}\cdot\dfrac{x-z}{x}\)
\(=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{y-x}{y}=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{-z}{y}=-1\)
TH2: y=z=-x
=>y+x+z=0(vô lý vì x,y,z đều dương)
Vậy: H=-1
Đúng 1
Bình luận (0)