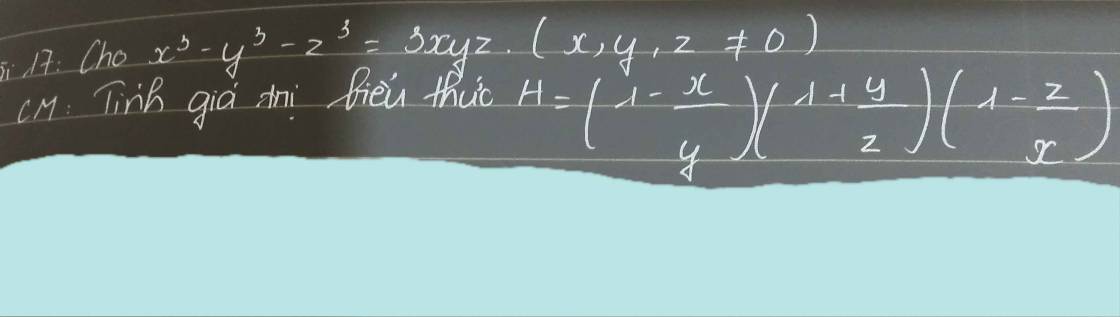\(x^3-y^3-z^3=3xyz\)
=>\(\left(x-y\right)^3-z^3+3xy\left(x-y\right)-3xyz=0\)
=>\(\left(x-y-z\right)\left[\left(x-y\right)^2+z\left(x-y\right)+z^2\right]+3xy\left(x-y-z\right)=0\)
=>\(\left(x-y-z\right)\left[x^2-2xy+y^2+xz-zy+z^2+3xy\right]=0\)
=>\(\left(x-y-z\right)\left(x^2+y^2+z^2+xy+xz-yz\right)=0\)
=>\(\left(x-y-z\right)\left(2x^2+2y^2+2z^2+2xy+2xz-2yz\right)=0\)
=>\(\left(x-y-z\right)\left[\left(x^2+2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(x^2+2xz+z^2\right)\right]=0\)
=>\(\left(x-y-z\right)\left[\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2\right]=0\)
=>\(\left[{}\begin{matrix}x-y-z=0\\\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=y+z\\y=z=-x\end{matrix}\right.\)
\(H=\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1-\dfrac{z}{x}\right)\)
\(=\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}\cdot\dfrac{x-z}{x}\)
TH1: x=y+z
=>\(H=\dfrac{y-x}{y}\cdot\dfrac{x}{z}\cdot\dfrac{x-z}{x}\)
\(=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{y-x}{y}=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{-z}{y}=-1\)
TH2: y=z=-x
=>y+x+z=0(vô lý vì x,y,z đều dương)
Vậy: H=-1