tìm giá trị lớn nhất của các biểu thức sau :
a . A = -x2 + 4x +2
b. B = x - x2 + 2
tìm giá trị lớn nhất của các biểu thức sau :
a . A = -x2 + 4x +2
b. B = x - x2 + 2
a.
\(A=-\left(x^2-4x-2\right)=-\left(x^2-4x+4-6\right)\\ =-\left(x-2\right)^2+6\le6\)
GTLN của A đạt 6 khi và chỉ khi `x=2`
b.
\(B=-\left(x^2-x-2\right)=-\left(x^2-2.\dfrac{1}{2}x+\dfrac{1}{4}-\dfrac{9}{4}\right)\\ =-\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}\le\dfrac{9}{4}\)
GTLN của B đạt \(\dfrac{9}{4}\) khi và chỉ khi \(x=\dfrac{1}{2}\)
a) \(A=-x^2+4x+2\)
\(A=-\left(x^2-4x-2\right)\)
\(A=-\left[\left(x-2\right)^2-6\right]\)
\(A=-\left(x-2\right)^2+6\)
Mà: \(-\left(x-2\right)^2\le0\forall x\) nên
\(A=-\left(x-2\right)^2+6\le6\)
Dấu "=" xảy ra:
\(-\left(x-2\right)^2+6=6\Leftrightarrow x=2\)
Vậy: \(A_{max}=6\) khi \(x=2\)
b) \(B=x-x^2+2\)
\(B=-\left(x^2-x-2\right)\)
\(B=-\left[\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{4}\right]\)
\(B=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}\)
Mà: \(-\left(x-\dfrac{1}{2}\right)^2\le0\forall x\)
Nên: \(B=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}\le\dfrac{9}{4}\forall x\)
Dấu "=" xảy ra:
\(-\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}=\dfrac{9}{4}\Leftrightarrow x=\dfrac{1}{2}\)
Vậy: \(B_{max}=\dfrac{9}{4}\) khi \(x=\dfrac{1}{2}\)
tìm giá trị nhỏ nhất của các biểu thức sau
a. A = x2 - 4x + 6
b. B = y2 - y + 1
c . C = x2 - 4x + y2 - y + 5
a.
\(A=x^2-4x+4+2=\left(x-2\right)^2+2\ge2\)
GTNN của A đạt 2 khi và chỉ khi \(x=2\)
b.
\(B=y^2-2.\dfrac{1}{2}y+\dfrac{1}{4}+\dfrac{3}{4}=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
GTNN của B đạt \(\dfrac{3}{4}\) khi và chỉ khi \(y=\dfrac{1}{2}\)
c.
\(C=x^2-4x+4+y^2-2.\dfrac{1}{2}y+\dfrac{1}{4}+\dfrac{3}{4}\\ =\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
GTNN của C đạt \(\dfrac{3}{4}\) khi và chỉ khi \(\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
a) \(A=x^2-4x+6\)
\(A=x^2-4x+4+2\)
\(A=\left(x-2\right)^2+2\)
Mà: \(\left(x-2\right)^2\ge0\forall x\) nên \(A=\left(x-2\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra:
\(\left(x-2\right)^2+2=2\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)
Vậy: \(A_{min}=2\) khi \(x=2\)
b) \(B=y^2-y+1\)
\(B=y^2-2\cdot\dfrac{1}{2}\cdot y+\dfrac{1}{4}+\dfrac{3}{4}\)
\(B=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(y-\dfrac{1}{2}\right)^2\ge\forall x\) nên \(B=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu "=" xảy ra:
\(\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\dfrac{3}{4}\Leftrightarrow y-\dfrac{1}{2}=0\)
\(\Leftrightarrow y=\dfrac{1}{2}\)
Vậy \(B_{min}=\dfrac{3}{4}\) khi \(y=\dfrac{1}{2}\)
c) \(C=x^2-4x+y^2-y+5\)
\(C=x^2-4x+4+y^2-y+\dfrac{1}{4}+\dfrac{3}{4}\)
\(C=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left\{{}\begin{matrix}\left(x-2\right)^2\ge0\forall x\\\left(y-\dfrac{1}{2}\right)^2\ge0\forall x\end{matrix}\right.\) nên
\(C=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu "=" xảy ra:
\(\left\{{}\begin{matrix}x-2=0\\y-\dfrac{1}{2}=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: \(C_{min}=\dfrac{3}{4}\) khi \(\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
tính giá trị biểu thức
a. N = x2 - 10x + 25 tại x = 55
b. P = x4 / 4 - x2y + y2 tại x = 4 ; y = 1/2
a) \(N=x^2-10x+25\)
\(N=x^2-2\cdot5\cdot x+5^2\)
\(N=\left(x-5\right)^2\)
Thay x = 55 vào N ta có:
\(N=\left(55-5\right)^2=2500\)
b) \(P=\dfrac{x^4}{4}-x^2y+y^2\)
\(P=\left(\dfrac{x^2}{2}\right)^2-2\cdot\dfrac{x^2}{2}\cdot y+y^2\)
\(P=\left(\dfrac{x^2}{2}-y\right)^2\)
Thay x = 4 và \(y=\dfrac{1}{2}\) vào P ta có:
\(P=\left(\dfrac{4^2}{2}-\dfrac{1}{2}\right)^2=\dfrac{225}{4}\)
Viết các đa thức sau dưới dạng bình phương của một tổng hoặc hiệu
4x2 + 4x + 1
\(4x^2+4x+1\)
\(=\left(2x\right)^2+2\cdot2x\cdot1+1^2\)
\(=\left(2x+1\right)^2\)
Tìm x
X+5=x(x+5)^2
X(x-2)=(x-2)
a: x(x+5)^2=x+5
=>(x+5)(x^2+5x-1)=0
=>x+5=0 hoặc x^2+5x-1=0
=>\(x\in\left\{-5;\dfrac{-5+\sqrt{29}}{2};\dfrac{-5-\sqrt{29}}{2}\right\}\)
b: x(x-2)=(x-2)
=>(x-2)(x-1)=0
=>x=2 hoặc x=1
Phân tích đa thức thành phân tử x^2-xy+y-y
Sửa đề: x^2-xy+x-y
=(x^2-xy)+(x-y)
=x(x-y)+(x-y)
=(x-y)(x+1)
Phân tích đa thức thành phân tử x(x-y)+x-2
Cái này không phân tích được nha bạn
Bài tập: Phân tích đa thức thành nhân tử (bài tổng hợp)
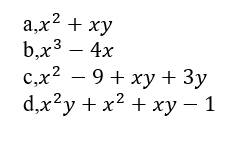
a) x² + xy
= x(x + y)
b) x³ - 4x
= x(x² - 4)
= x(x - 2)(x + 2)
c) x² - 9 + xy + 3y
= (x² - 9) + (xy + 3y)
= (x - 3)(x + 3) + y(x + 3)
= (x + 3)(x + y - 3)
d) x²y + x² + xy - 1
= (x²y + xy) + (x² - 1)
= xy(x + 1) + (x - 1)(x + 1)
= (x + 1)(xy + x - 1)
x2 - 1 -2xy +2y
( x + 3 )2 - ( 2x - 5 ) x ( x + 3 )
( 3x + 2 )2 + ( 3x -2 )2 -2 ( 9x2 - 4 )
`x^2 -1-2xy+2y`
`=(x^2-1)-(2xy-2y)`
`=(x-1)(x+1)-2y(x-1)`
`=(x-1)(x+1-2y)`
__
`(x+3)^2-(2x-5)(x+3)`
`=(x+3)(x+3-2x+5)`
`=(x+3)(-x+8)`
__
`(3x+2)^2 +(3x-2)^2-2(9x^2-4)`
`= (3x+2)^2 +(3x-2)^2-2(3x-2)(3x+2)`
`= (3x+2)^2-2(3x-2)(3x+2)+(3x-2)^2`
`=[(3x+2)-(3x-2)]^2`
`=(3x+2-3x+2)^2`
`= 4^2=16`
\(x^2-1-2xy+2y\\ =\left(x^2-1\right)-\left(2xy-2y\right)\\ =\left(x-1\right)\left(x+1\right)-2y\left(x-1\right)\\ =\left(x-1\right)\left(x+1-2y\right)\)
\(\left(x+3\right)^2-\left(2x-5\right)\left(x+3\right)\\ =\left(x+3\right)\left(x+3-2x+5\right)\\ =\left(x+3\right)\left(8-x\right)\)
\(\left(3x+2\right)^2+\left(3x-2\right)^2-2\left(9x^2-4\right)\\ =9x^2+12x+4+9x^2-12x+4-18x^2+8\\ =4+4+8\\ =16\)
1) 10a³ - 10a 2) 5xy - 40a³b³ xy 3) 5a² + 10ab + 5b² 4) 6p² - 12p + 6 5) m² + 2mn + n² - p² 6) 54x³ + 16y³ 7) 1 - m² + 2mn - b²
1: =10(a^3-a)
=10a(a^2-1)
=10a(a-1)(a+1)
2: \(=5xy\left(1-8a^3b^3\right)\)
\(=5xy\left(1-2ab\right)\left(1+2ab+4a^2b^2\right)\)
3: \(=5\left(a^2+2ab+b^2\right)=5\left(a+b\right)^2\)
4: \(=6\left(p^2-2p+1\right)=6\left(p-1\right)^2\)
5: =(m+n)^2-p^2
=(m+n-p)(m+n+p)
6: =2(27x^3+8y^3)
=2(3x+2y)(9x^2-6xy+4y^2)
1) 10a³ - 10a
= 10a(a² - 1)
= 10a(a - 1)(a + 1)
2) 5xy - 40a³b³xy
= 5xy(1 - 8a³b³)
= 5xy(1 - 2ab)(1 + 2ab + 4a²b²)
3) 5a² + 10ab + 5b²
= 5(a² + 2ab + b²)
= 5(a + b)²
4) 6p² - 12p + 6
= 6(p² - 2p + 1)
= 6(p - 1)²
5) m² + 2mn + n² - p²
= (m + n)² - p²
= (m + n - p)(m + n + p)
6) 54x³ + 16y³
= 2(27x³ + 8y³)
= 2[(3x)³ + (2y)³]
= 2(3x + 2y)(9x² - 6xy + 4y²)
7) Sửa đề:
1 - m² + 2mn - n²
= 1 - (m² - 2mn + n²)
= 1 - (m - n)²
= (1 + m - n)(1 - m + n)