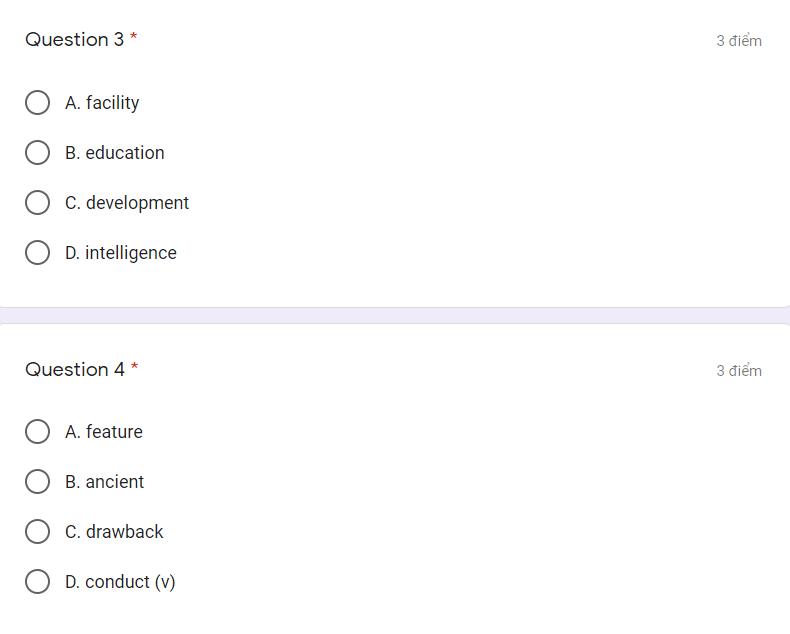
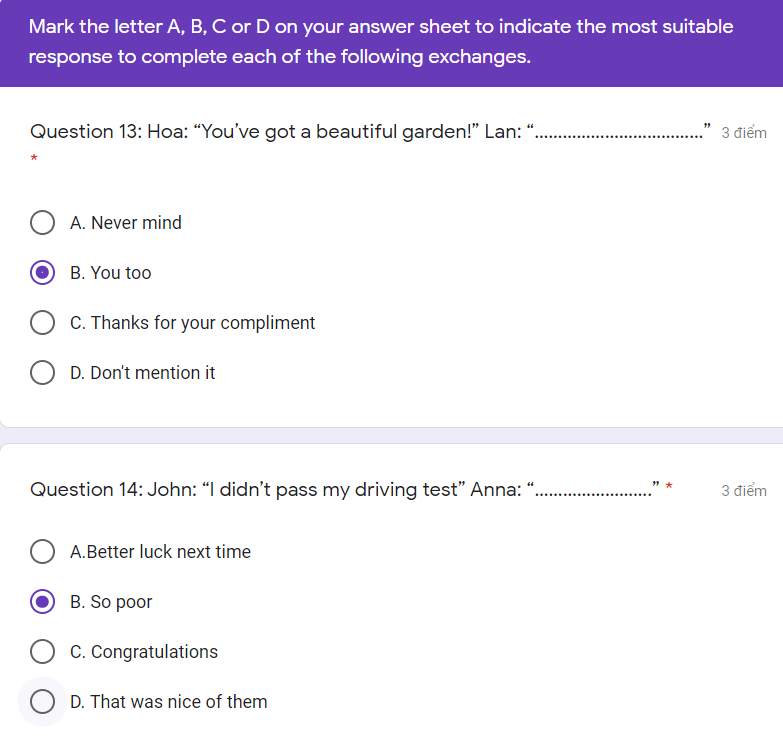
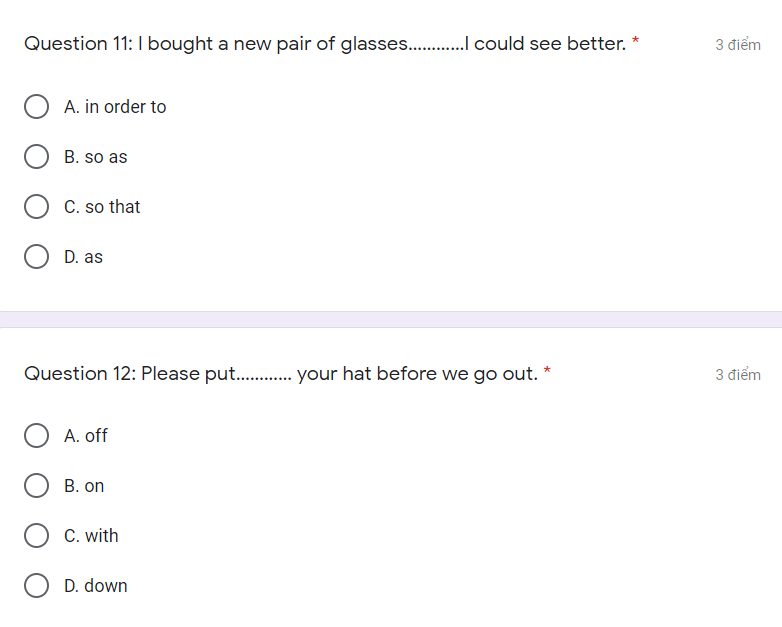
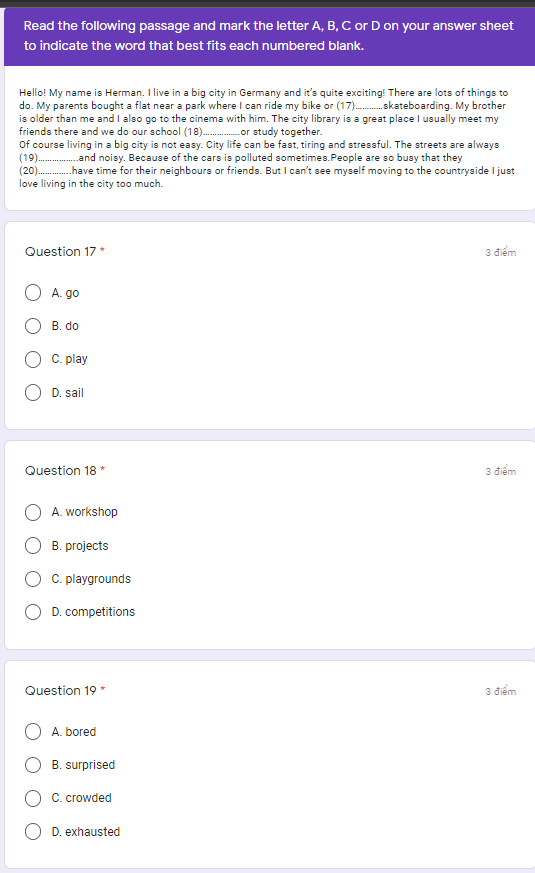
Mọi người khoanh giúp em mấy câu này với ạ
NC
Những câu hỏi liên quan
Mọi người check giúp em câu đã khoanh với ạ, sai thì chữa giúp em! Làm giúp câu chưa khoanh nữa ạ. Em cảm ơn!! 
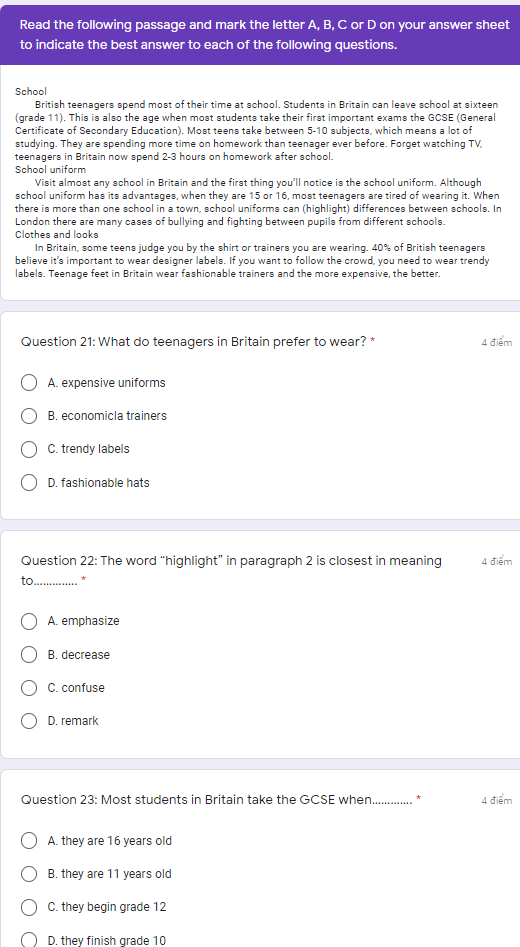
Para 1 - b
Para 2 - a
Para 3 - c
T - F - T - T - NG
1 B
2 A
3 D
4 D
5 A
Đúng 1
Bình luận (0)
Mọi người trình bày cách giải mấy câu này giúp em với ạ!!
Đọc tiếp
Mọi người trình bày cách giải mấy câu này giúp em với ạ!!

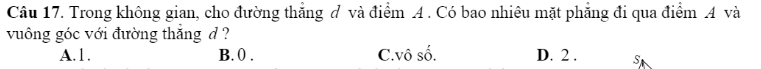
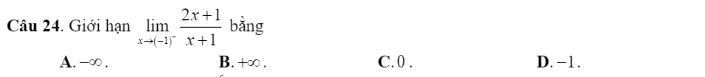

2.B (t/c của giới hạn)
6.B H/s ko x/đ với x = 0 -> Ko liên tục tại đ x = 0
17.C
24. \(\lim\limits_{x\rightarrow\left(-1\right)^-}\dfrac{2x+1}{x+1}\) . Thấy : \(\lim\limits_{x\rightarrow\left(-1\right)^-}2x+1=2.\left(-1\right)+1=-1\)
\(\lim\limits_{x\rightarrow\left(-1\right)^-}x+1=0\) ; \(x\rightarrow\left(-1\right)^-\Rightarrow x+1< 0\).
Do đó : \(\lim\limits_{x\rightarrow\left(-1\right)^-}=+\infty\) . Chọn B
Đúng 3
Bình luận (0)
33 . B
Trên (SAB) ; Lấy H là TĐ của AB ; ta có : SH \(\perp AB\) ( \(\Delta SAB\) đều ) ; HC \(\perp AB\) ( \(\Delta ABC\) đều )
Ta có : (SAB) \(\perp\left(ABC\right)\) ; \(\left(SAB\right)\cap\left(ABC\right)=AB;SH\perp AB\)
\(\Rightarrow SH\perp\left(ABC\right)\)
\(SC\cap\left(ABC\right)=C\) . Suy ra : \(\left(SC;\left(ABC\right)\right)=\widehat{SCH}\)
Có : \(SH\perp HC\) => \(\Delta SHC\) vuông tại H
G/s \(\Delta\)ABC đều có cạnh là a \(\Rightarrow AB=a\)
\(\Delta SAB\) đều => SA = SB = AB = a
Tính được : \(SH=HC=\dfrac{\sqrt{3}}{2}a\)
\(\Delta SHC\) vuông tại H : \(tan\widehat{SCH}=\dfrac{SH}{HC}=1\)
\(\Rightarrow\widehat{SCH}=45^o\) => ...
Đúng 3
Bình luận (0)
Mọi người giúp em mấy câu này với ạ!! Một vài câu cũng được mà làm hết thì càng tốt

4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
Đúng 1
Bình luận (0)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
Đúng 1
Bình luận (0)
7.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-\left(x+1\right)+\left(x+1-\sqrt[3]{1+3x}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{1+2x}+x+1}+\dfrac{x^2\left(x+3\right)}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{1+2x}+x+1}+\dfrac{x+3}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{3}{1+1+1}=1\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2x+3\right)=3\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Mọi người ơi giúp em câu 99 này với ạ ,để em áp dụng cho mấy bài sau 😊 😊😊
a) CuO + 2HCl → CuCl2 + H2O (1)
ZnO + 2HCl → ZnCl2 + H2O (2)
b) Gọi số mol CuO, ZnO lần lượt là x, y
mhh = mCuO + mZnO → 80x + 81y = 12,1 (*)
nHCl = 0,1 . 3 = 0,3 mol
Theo (1): nHCl (1) = 2nCuO = 2x
Theo (2): nHCl (2) = 2nZnO = 2y
nHCl = 2x + 2y = 0,3 (**)
Từ (*) và (**) → x = 0,05; y = 0,1
%mCuO=0,05.8012,1.100%=33,06%%mZnO=100%−33,06%=66,94%%mCuO=0,05.8012,1.100%=33,06%%mZnO=100%−33,06%=66,94%
c) CuO + H2SO4 → CuSO4 + H2O
0,05 → 0,05
ZnO + H2SO4 → ZnSO4 + H2O
0,1 → 0,1
nH2SO4 = 0,05 + 0,1 = 0,15 mol
mH2SO4 = 0,15 . 98 = 14,7g
mdd H2SO4 = 14,7 : 20% = 73,5(g)
cho mik xin 1 like zới đc khum:))
Đúng 1
Bình luận (0)
Mọi người ơi giúp em trả lời mấy câu này vs ạ ..em cảm ơn ạ

1, A
2, A
3, B
4, B
5, A
6, C
7, A
8, B
9, A
10, B
11, C
12, D
Đúng 0
Bình luận (0)
mọi người giúp em mấy bài này với ạ =(((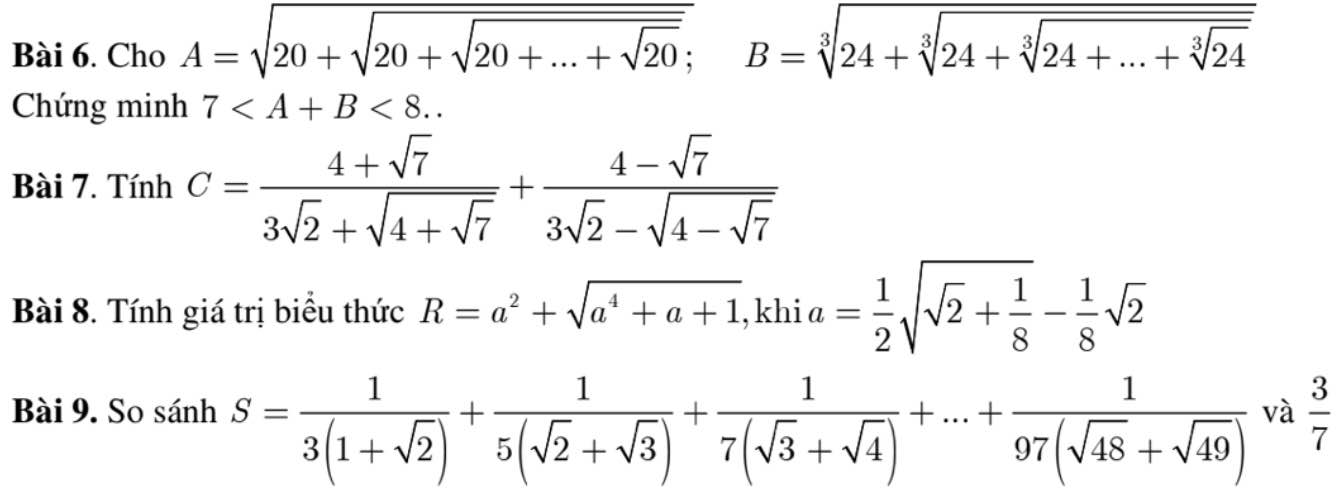
Bài 7:
Ta có: \(C=\dfrac{4+\sqrt{7}}{3\sqrt{2}+\sqrt{4+\sqrt{7}}}+\dfrac{4-\sqrt{7}}{3\sqrt{2}-\sqrt{4-\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{6+\sqrt{8+2\sqrt{7}}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{6-\sqrt{8-2\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{7+\sqrt{7}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{7-\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{7}-1\right)\left(4+\sqrt{7}\right)}{6\sqrt{7}}+\dfrac{\sqrt{2}\left(\sqrt{7}+1\right)\left(4-\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(-3+3\sqrt{7}+3+3\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\sqrt{2}\)
Đúng 2
Bình luận (0)
6.
Ta có:
\(A=\sqrt{20+\sqrt{20+...+\sqrt{20}}}>\sqrt{20+\sqrt{\dfrac{1}{16}}}=\dfrac{9}{2}\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}>\sqrt[3]{24}=\sqrt[3]{\dfrac{192}{8}}>\sqrt[3]{\dfrac{125}{8}}=\dfrac{5}{2}\)
\(\Rightarrow A+B>\dfrac{9}{2}+\dfrac{5}{2}=7\)
\(A=\sqrt[]{20+\sqrt[]{20+...+\sqrt[]{20}}}< \sqrt[]{20+\sqrt[]{20+...+\sqrt[]{25}}}=5\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}< \sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{27}}}=3\)
\(\Rightarrow A+B< 5+3=8\)
Đúng 1
Bình luận (0)
8.
Ta có:
\(a=\dfrac{1}{2}\sqrt{\sqrt{2}+\dfrac{1}{8}}-\dfrac{\sqrt{2}}{8}\Rightarrow\dfrac{1}{2}\sqrt{\sqrt{2}+\dfrac{1}{8}}=a+\dfrac{\sqrt{2}}{8}\)
\(a^2=\dfrac{1}{4}\left(\sqrt{2}+\dfrac{1}{8}\right)+\dfrac{1}{32}-\dfrac{\sqrt{2}}{4}.\dfrac{1}{2}\sqrt{\sqrt{2}+\dfrac{1}{8}}\)
\(=\dfrac{\sqrt{2}}{4}+\dfrac{1}{32}+\dfrac{1}{32}-\dfrac{\sqrt{2}}{4}\left(a+\dfrac{\sqrt{2}}{8}\right)\)
\(=\dfrac{\sqrt{2}}{4}+\dfrac{1}{16}-\dfrac{\sqrt{2}}{4}a-\dfrac{1}{16}\)
\(=\dfrac{\sqrt{2}}{4}\left(1-a\right)\)
\(\Rightarrow a^4=\dfrac{1}{8}\left(a^2-2a+1\right)\)
\(\Rightarrow a^4+a+1=\dfrac{1}{8}\left(a^2-2a+1\right)+a+1=\dfrac{1}{8}\left(a+3\right)^2\)
\(\Rightarrow R=a^2+\dfrac{\sqrt{2}}{4}\left(a+3\right)=\dfrac{\sqrt{2}}{4}\left(1-a\right)+\dfrac{\sqrt{2}}{4}\left(a+3\right)=\sqrt{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
mọi người giúp em làm câu này với ạ cảm ơn mọi người nhiêu ạ

C NHA BN CÂU 45 KO LÀM ĐC
Mọi ơi giúp e giải mấy câu này với ạ! Em cần gấp!
2. There used to have many old buildings 10 years ago
3. I wish a new mall didn't build
4. I have had this wardrobe since my wedding day
5. She hasn't been seen for two years
Đúng 3
Bình luận (0)
2. There used to be many old buildings 10 years ago.
3. I wish a new mall weren't built here.
4. I have bought this wardrobe since my wedding day.
5. She hasn't been seen (by me) for two years.
Đúng 3
Bình luận (0)
Mọi người giúp mình giải mấy câu này với ạ! Mình cần gấp trước 10h tối ạ!
1.
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
2.
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 2
Bình luận (0)
3.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{5}{8}\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{2\pi}{3}+k2\pi\\4x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
4.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\dfrac{1}{4}\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x=\dfrac{1}{4}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{1}{4}\)
\(\Leftrightarrow cos4x=-1\)
\(\Leftrightarrow4x=\pi+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Moij người giúp em xem xem mấy câu khoanh đúng chưa ạ,ai giải đc mấy cái kia giúp vs :))
Đọc tiếp
Moij người giúp em xem xem mấy câu khoanh đúng chưa ạ,ai giải đc mấy cái kia giúp vs :))