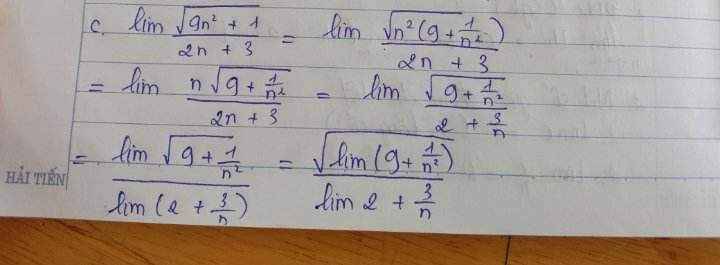4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
7.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-\left(x+1\right)+\left(x+1-\sqrt[3]{1+3x}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{1+2x}+x+1}+\dfrac{x^2\left(x+3\right)}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{1+2x}+x+1}+\dfrac{x+3}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{3}{1+1+1}=1\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2x+3\right)=3\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
9.
\(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\left(\sqrt[]{1+x^2}+x\right)^4-\left(\sqrt[]{1+x^2}-x\right)^4}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\left[\left(\sqrt[]{1+x^2}+x\right)^2+\left(\sqrt[]{1+x^2}-x\right)^2\right]\left[\left(\sqrt[]{1+x^2}+x\right)^2-\left(\sqrt[]{1+x^2}-x\right)^2\right]}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\left[\left(\sqrt[]{1+x^2}+x\right)^2+\left(\sqrt[]{1+x^2}-x\right)^2\right].2\sqrt[]{1+x^2}.2x}{x}\)
\(=\lim\limits_{x\rightarrow0}4\sqrt[]{1+x^2}.\left[\left(\sqrt[]{1+x^2}+x\right)^2+\left(\sqrt[]{1+x^2}-x\right)^2\right]\)
\(=4.1.\left(1+1\right)=8\)
\(f\left(0\right)=3.0+8=8\)
\(\Rightarrow\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\)
Hàm liên tục tại \(x=0\)
8.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\left(1+2020x\right)^{2021}-\left(1+2021x\right)^{2020}}{2021x^2}\)
(Mũ quá to nên thêm bớt HĐT hoặc khai triển nhị thức Newton sẽ tạo ra 1 biểu thức phức tạp, do đó để đơn giản chúng ta sẽ sử dụng quy tắc L'Hopital để tính giới hạn)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{2020.2021\left(1+2020x\right)^{2020}-2020.2021\left(1+2021x\right)^{2019}}{2.2021x}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{2020\left(1+2020x\right)^{2020}-2020\left(1+2021x\right)^{2019}}{2x}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{2020^3\left(1+2020x\right)^{2019}-2019.2020.2021\left(1+2021x\right)^{2018}}{2}\)
\(=\dfrac{2020^3-2019.2020.2021}{2}=1010\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x^2+1010\right)=1010\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\)Hàm liên tục tại \(x=0\)
Câu 8 ko để ý kĩ đề, sửa lại đoạn \(\lim\limits_{x\rightarrow0^+}...\) thành \(\lim\limits_{x\rightarrow0}...\) và \(\lim\limits_{x\rightarrow0^-}...\) thành \(f\left(0\right)\)
10.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\dfrac{\left(\sqrt[]{x}-1\right)\left(\sqrt[3]{x}-1\right)\left(\sqrt[4]{x}-1\right)}{\left(x^2-1\right)^3}\)
\(=\lim\limits_{x\rightarrow1^+}\dfrac{\dfrac{\left(x-1\right)}{\sqrt[]{x}+1}.\dfrac{x-1}{\sqrt[3]{x^2}+\sqrt[3]{x}+1}.\dfrac{x-1}{\left(\sqrt[4]{x}+1\right)\left(\sqrt[]{x}+1\right)}}{\left(x-1\right)^3\left(x+1\right)^3}\)
\(=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\left(x+1\right)^3\left(\sqrt[]{x}+1\right)\left(\sqrt[3]{x^2}+\sqrt[3]{x}+1\right)\left(\sqrt[4]{x}+1\right)\left(\sqrt[]{x}+1\right)}\)
\(=\dfrac{1}{2^3.2.3.2.2}=\dfrac{1}{192}\)
\(f\left(1\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(3-x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)\ne\lim\limits_{x\rightarrow1^-}f\left(x\right)\)
Hàm gián đoạn tại \(x=1\)