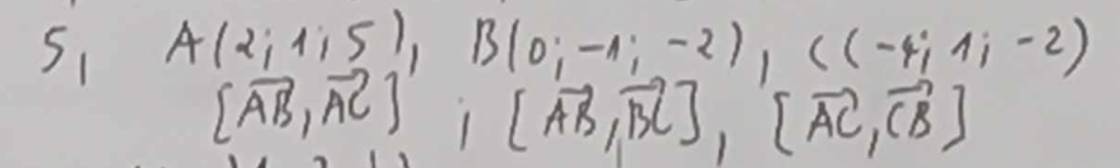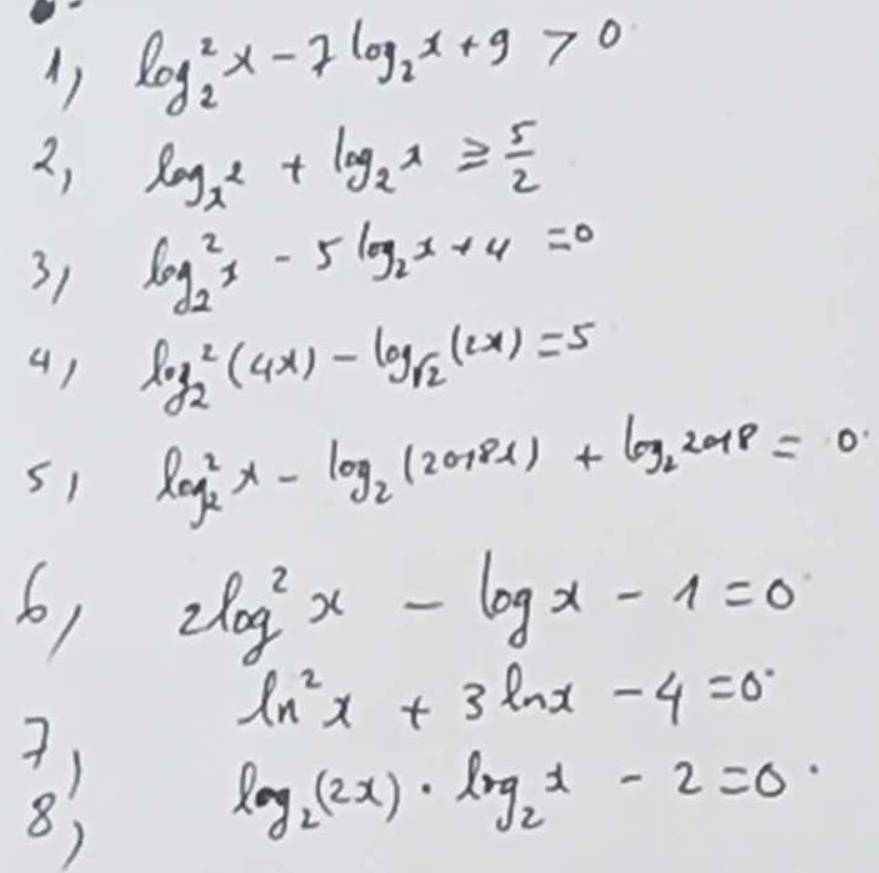Gọi \(x_1\), \(x_2\) là các nghiệm phương trình \(\log^2_5x-4\log_5x+2=0\). Tính \(x_1x_2\).
Ôn tập cuối năm môn Đại số 11
Đặt \(log_5x=t\) \(\Rightarrow x=5^t\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}t_1+t_2=4\\t_1t_2=2\end{matrix}\right.\)
\(\Rightarrow x_1x_2=5^{t_1}.5^{t_2}=5^{t_1+t_2}=5^4=625\)
Đúng 1
Bình luận (0)
Cho 2 số thực dương \(a\), \(b\) thỏa mãn \(\log_{20}a=\log_8b=\log_{125}\left(5a+12b\right)\). Tính \(P=\dfrac{a+b}{b}\).
Đặt \(log_{20}a=log_8b=log_{125}\left(5a+12b\right)=k\)
\(\Rightarrow\left\{{}\begin{matrix}a=20^k\\b=8^k\\5a+12b=125^k\end{matrix}\right.\)
\(\Rightarrow5.20^k+12.8^k=125^k\)
\(\Rightarrow5.\left(\dfrac{4}{25}\right)^k+12.\left(\dfrac{8}{125}\right)^k=1\)
Đặt \(\left(\dfrac{2}{5}\right)^k=x>0\)
\(\Rightarrow5x^2+12x^3=1\)
\(\Leftrightarrow\left(3x-1\right)\left(4x^2+3x+1\right)=0\)
\(\Leftrightarrow x=\dfrac{1}{3}\)
\(\Rightarrow\left(\dfrac{2}{5}\right)^k=\dfrac{1}{3}\)
\(P=\dfrac{a+b}{b}=\dfrac{a}{b}+1=\dfrac{20^k}{8^k}+1=\left(\dfrac{5}{2}\right)^k+1=3+1=4\)
Đúng 2
Bình luận (0)
Để đầu tư mở rộng kinh doanh, cô Ba vay ngân hàng số tiền 200 triệu đồng với lãi suất 1% / tháng. Cô Ba muốn hoàn nơ cho ngân hàng theo cách sau: sau đùng một tháng kể từ ngày vay, cô bắt đầu hoàn nợ; hai lần hoàn ng liên tiếp cách nhau đúng 1 tháng, số tiền hoàn nợ ở mỗi lần là như nhau và cô Ba trả hết nợ sau đúng 6 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền X mà cô Ba phải trả cho ngân hàng mỗi tháng là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời gian cô Ba hoàn nợ...
Đọc tiếp
Để đầu tư mở rộng kinh doanh, cô Ba vay ngân hàng số tiền 200 triệu đồng với lãi suất 1% / tháng. Cô Ba muốn hoàn nơ cho ngân hàng theo cách sau: sau đùng một tháng kể từ ngày vay, cô bắt đầu hoàn nợ; hai lần hoàn ng liên tiếp cách nhau đúng 1 tháng, số tiền hoàn nợ ở mỗi lần là như nhau và cô Ba trả hết nợ sau đúng 6 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền X mà cô Ba phải trả cho ngân hàng mỗi tháng là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời gian cô Ba hoàn nợ.
Gọi A là số tiền vay (ở đây là 200tr), r% là lãi suất hàng tháng, X là số tiền hoàn nợ mỗi tháng.
Sau tháng thứ nhất, số tiền nợ ngân hàng là: \(A.\left(1+r\right)^1\) (triệu)
Sau đó trả X triệu nên số tiền nợ là: \(S_1=A\left(1+r\right)^1-X=A\left(1+r\right)^1-X.\dfrac{\left(1+r\right)^1-1}{r}\)
Cuối tháng thứ hai, số tiền nợ ngân hàng là: \(\left[A\left(1+r\right)^1-X\right].\left(1+r\right)=A\left(1+r\right)^2-X\left(1+r\right)\)
Trả tiếp X triệu nên số tiền nợ là: \(S_2=A\left(1+r\right)^2-X\left(1+r\right)-X=A.\left(1+r\right)^2-X.\dfrac{\left(1+r\right)^2-1}{r}\)
Theo quy luật trên, sau n tháng thì số tiền nợ ngân hàng là:
\(S_n=A.\left(1+r\right)^n-X.\dfrac{\left(1+r\right)^n-1}{r}\)
Do trả hết sau \(n=6\) tháng nên \(S_6=0\)
\(\Rightarrow200\left(1+1\%\right)^6-X.\dfrac{\left(1+1\%\right)^6-1}{1\%}=0\)
\(\Rightarrow X\approx34,51\) (triệu đồng)
Đúng 1
Bình luận (0)
Ông Năm gửi tiết kiệm số tiền 10 triệu đồng ở một ngân hàng với lãi suất 5%/năm theo hình thức lãi kép. Hỏi sau 10 năm thì ông Năm nhận được số tiền cả vốn lẫn lãi là bao nhiêu?
Số tiền nhận được sau 10 năm là:
\(10tr.\left(1+5\%\right)^{10}=16288946\) (đồng)
Đúng 1
Bình luận (0)
Xét các số thực x, y thỏa mãn log_2left(x+sqrt{x^2+1}right)+log_2left(y+sqrt{y^2+1}right)4. Kí hiệu m là giá trị nhỏ nhất Px+y. Mệnh đề nào sau đây đúng?A. minleft(4;5right)B. minleft(3;dfrac{7}{2}right)C. minleft(dfrac{7}{2};4right)D. minleft(dfrac{5}{2};3right)
Đọc tiếp
Xét các số thực \(x\), \(y\) thỏa mãn \(\log_2\left(x+\sqrt{x^2+1}\right)+\log_2\left(y+\sqrt{y^2+1}\right)=4\). Kí hiệu \(m\) là giá trị nhỏ nhất \(P=x+y\). Mệnh đề nào sau đây đúng?
A. \(m\in\left(4;5\right)\)
B. \(m\in\left(3;\dfrac{7}{2}\right)\)
C. \(m\in\left(\dfrac{7}{2};4\right)\)
D. \(m\in\left(\dfrac{5}{2};3\right)\)
\(log_2\left(x+\sqrt{x^2+1}\right)+log_2\left(y+\sqrt{y^2+1}\right)=4\)
\(\Leftrightarrow log_2\left[\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)\right]=4\)
\(\Leftrightarrow\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=16\)
Đặt \(\left\{{}\begin{matrix}x+\sqrt{x^2+1}=a>0\\y+\sqrt{y^2+1}=b>0\end{matrix}\right.\) \(\Rightarrow ab=16\)
\(\sqrt{x^2+1}=a-x\Rightarrow x^2+1=a^2-2ax+x^2\)
\(\Rightarrow2ax=a^2-1\Rightarrow x=\dfrac{a^2-1}{2a}\)
Tương tự \(\Rightarrow y=\dfrac{b^2-1}{2b}\)
\(P=x+y=\dfrac{a^2-1}{2a}+\dfrac{b^2-1}{2b}=\dfrac{a+b}{2}-\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
\(=\dfrac{a+b}{2}-\dfrac{1}{2}\left(\dfrac{a+b}{ab}\right)=\dfrac{a+b}{2}-\dfrac{a+b}{32}\) (do \(ab=16\))
\(=\dfrac{15}{32}\left(a+b\right)\ge\dfrac{15}{32}.2\sqrt{ab}=\dfrac{15}{32}.2\sqrt{16}=\dfrac{15}{4}\)
\(\Rightarrow m=\dfrac{15}{4}=3,75\) (C đúng)
Đúng 2
Bình luận (0)
Cho các số thực dương \(x\), \(y\) thỏa mãn \(\log_{x+y}\left(x^2+y^2\right)\le1\). Giá trị lớn nhất biểu thức \(A=6\left(x+y\right)^2-14\left(x+y\right)+44\) là?
Nếu \(0< x+y< 1\)
Do \(0< x+y< 1\Rightarrow\left\{{}\begin{matrix}0< x< 1\\0< y< 1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x^2< x\\y^2< y\end{matrix}\right.\)
\(\Rightarrow1>x+y>x^2+y^2\)
\(\Rightarrow log_{x+y}\left(x^2+y^2\right)>1\) (trái với giả thiết)
\(\Rightarrow x+y>1\)
Khi đó ta có: \(log_{x+y}\left(x^2+y^2\right)\le1\Leftrightarrow x+y\ge x^2+y^2\ge\dfrac{1}{2}\left(x+y\right)^2\)
\(\Rightarrow x+y\le2\)
Đặt \(x+y=a\Rightarrow1< a\le2\)
\(A=6a^2-14a+44=6a^2-14a+4+40=2\left(a-2\right)\left(3a-1\right)+40\)
Do \(1< a\le2\Rightarrow\left\{{}\begin{matrix}a-2\le0\\3a-1>0\end{matrix}\right.\) \(\Rightarrow\left(a-2\right)\left(3a-1\right)\le0\)
\(\Rightarrow A\le40\)
\(A_{max}=40\) khi \(a=2\) hay \(x=y=1\)
Đúng 3
Bình luận (0)
1. tích có hướng vectơ
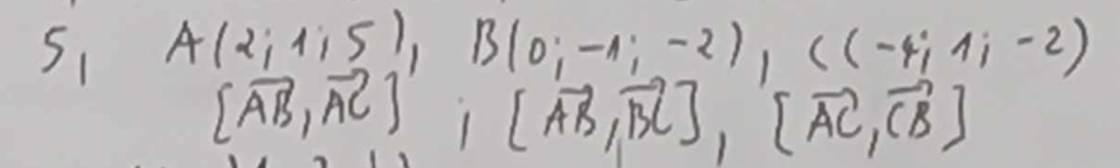
\(\left(\sqrt{5}+2\right)^{x-1}=\left(\sqrt{5}-2\right)^{\dfrac{x-1}{x+1}}\)
\(\left(\sqrt{5}+2\right)^{x-1}=\left(\sqrt{5}-2\right)^{\dfrac{x-1}{x+1}}\)
=>\(\left(\sqrt{5}+2\right)^{x-1}=\left(\sqrt{5}+2\right)^{\dfrac{-x+1}{x+1}}\)
=>\(x-1=\dfrac{-x+1}{x+1}\)
=>\(\left(x-1\right)\left(1+\dfrac{1}{x+1}\right)=0\)
=>\(\left[{}\begin{matrix}x-1=0\\x+1=-1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
3: \(log_2^2x-5\cdot log_2x=4=0\)
=>\(\left(log_2x-1\right)\left(log_2x-4\right)=0\)
=>\(\left[{}\begin{matrix}log_2x-1=0\\log_2x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}log_2x=1\\log_2x=4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
6: \(2\cdot log^2x-logx-1=0\)
=>\(2\cdot log^2x-2logx+logx-1=0\)
=>\(\left(logx-1\right)\left(2logx+1\right)=0\)
=>\(\left[{}\begin{matrix}logx=1\left(nhận\right)\\logx=-\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\Leftrightarrow logx=1\)
=>\(x=10\)
7: \(ln^2x+3lnx-4=0\)
=>\(\left(lnx+4\right)\left(lnx-1\right)=0\)
=>\(\left[{}\begin{matrix}lnx+4=0\\lnx-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}lnx=-4\\lnx=1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=e^{-4}\\x=e^1=e\end{matrix}\right.\)
2:
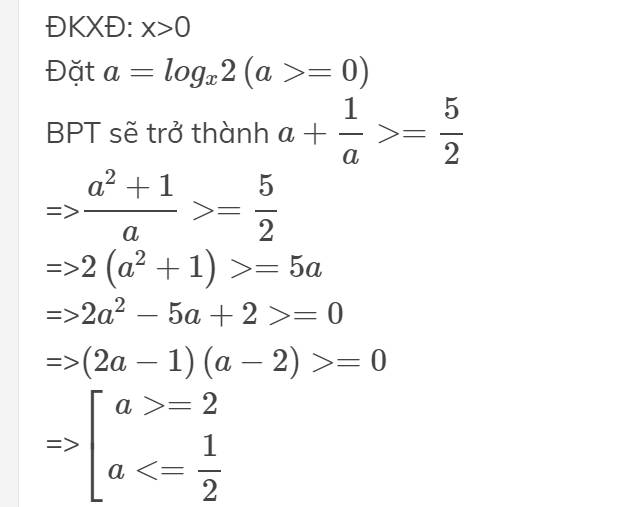
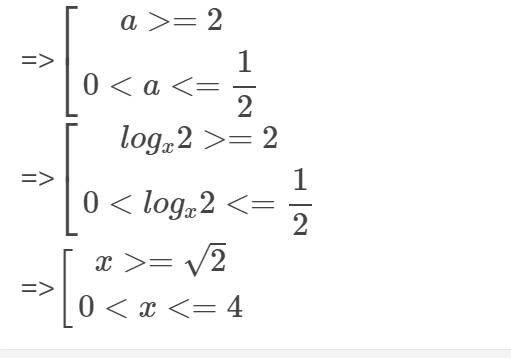
4:
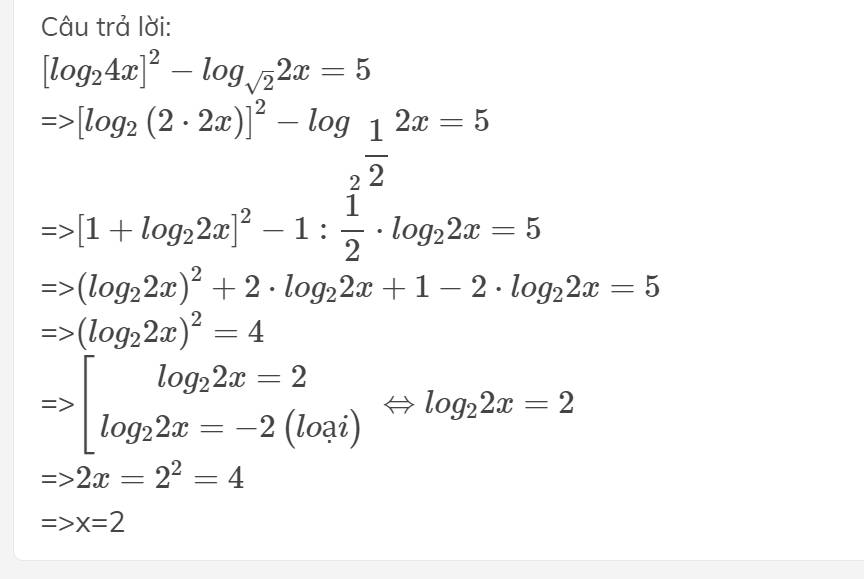
Đúng 1
Bình luận (0)