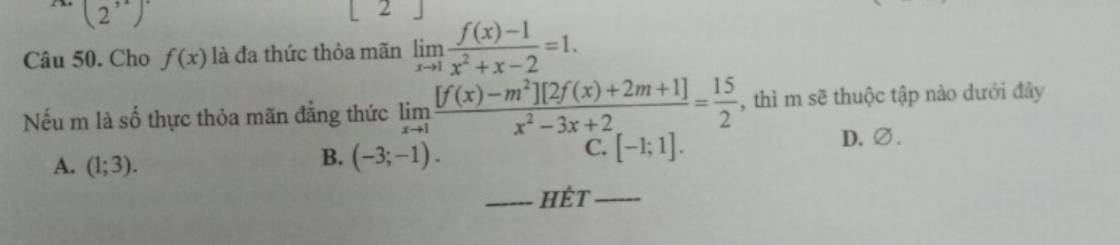Chương 4: GIỚI HẠN

Chọn \(f\left(x\right)=3x-2\)

Giới hạn đã cho hữu hạn khi \(\left[{}\begin{matrix}3x-2-m^2=0\\2.\left(3x-2\right)+2m+1=0\end{matrix}\right.\) có nghiệm \(x=1\)

TH1: \(3x-2-m^2=0\) có nghiệm \(x=1\Rightarrow m^2=1\Rightarrow m=\pm1\)

Với \(m=1\Rightarrow\lim\limits_{x\rightarrow1}\dfrac{\left(3x-3\right)\left(6x-1\right)}{x^2-3x+2}=-15\left(ktm\right)\)

Với \(m=-1\Rightarrow\lim\limits_{x\rightarrow1}\dfrac{\left(3x-3\right)\left(6x-5\right)}{x^2-3x+2}=-3\left(ktm\right)\)

TH2: \(2\left(3x-2\right)+2m+1=0\) có nghiệm \(x=1\)

\(\Rightarrow m=-\dfrac{3}{2}\)

\(\lim\limits_{x\rightarrow1}\dfrac{\left(3x-2-\dfrac{9}{4}\right)\left(6x-6\right)}{x^2-3x+2}=\dfrac{15}{2}\) (thỏa mãn)

Vậy \(m=-\dfrac{3}{2}\)

Giả thiết suy ra \(f\left(1\right)=1\)

Giới hạn \(\dfrac{\left[f\left(x\right)-m^2\right].\left[2f\left(x\right)+2m+1\right]}{x^2-3x+2}\) hữu hạn nên \(\left[f\left(x\right)-m^2\right]\left[2f\left(x\right)+2m+1\right]=0\) có nghiệm \(x=1\)

\(\Rightarrow\left[f\left(1\right)-m^2\right].\left[2f\left(1\right)+2m+1\right]=0\)

\(\Rightarrow\left(1-m^2\right)\left(2m+3\right)=0\)

\(\Rightarrow m=\left\{-\dfrac{3}{2};-1;1\right\}\)

Lần lượt thay 3 giá trị ta được \(m=-\dfrac{3}{2}\) thỏa mãn (đến đoạn này biện pháp tốt nhất là chọn hàm \(f\left(x\right)=x^2+x-1\) rồi CALC là 3s xong kết quả chứ tính tay 3 con giới hạn chắc hết ngày)

Giới hạn đến 2- thì là x nhỏ hơn 2, giới hạn đến 2+ thì là lớn hơn 2

Mà thật ra là bạn chỉ nên quan đến khi x tiến đến 2- hay 2+ khi có dấu căn hoặc là giá trị tuyệt đối thôi, còn trong những dạng này thì thay như bình thường. Mẫu bằng 0 thì xem trên tử, tử bằng 0 thì biến đổi hoặc tử khác 0 thì sẽ ra kết quả luôn

\(\lim\limits_{x\rightarrow2^-}\dfrac{3x^2+x-1}{2x^2-5x+2}\)

\(=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow2^-}3x^2+x-1=3\cdot2^2+2-1=3\cdot4+1=13>0\\\lim\limits_{x\rightarrow2^-}2x^2-5x+2=2\cdot2^2-5\cdot2+2=0\\\end{matrix}\right.\)

Giới hạn 1 phía thì gần như bạn kia nói (mặc dù cuối cùng lại kết luận sai). Với \(x\rightarrow2^-\) thì đồng nghĩa \(x< 2\), nên khi đó nhìn lên khu vực xét dấu của \(2x^2-5x+2\) ta sẽ biết nó âm hay dương.

Nếu giới hạn \(x\rightarrow2\) mà tử, mẫu có cùng nhân tử \(x-2\) (nghĩa là rút gọn được) thì làm bình thường. Còn nếu chỉ có mẫu tiến tới 0, tử tiến tới 1 số khác 0 thì có thể kết luận ngay là giới hạn này ko tồn tại (ngoại trừ trường hợp dấu của mẫu số ko đổi khi x đi qua 2, ví dụ như \(\left(2x^2-5x+2\right)^2\) thì nó luôn dương, hoặc \(\left|2x^2-5x+2\right|\) cũng vậy)

Ví dụ cụ thể: \(\lim\limits_{x\rightarrow2^-}\dfrac{3x^2+x-1}{2x^2-5x+2}=-\infty\)

\(\lim\limits_{x\rightarrow2}\dfrac{3x^2+x-1}{2x^2-5x+2}\) không tồn tại.

\(\lim\limits_{x\rightarrow2}\dfrac{3x^2+x-1}{\left|2x^2-5x+2\right|}=+\infty\)

\(\lim\limits_{x\rightarrow2}\dfrac{3x^2+x-1}{-\left(2x^2-5x+2\right)^2}=-\infty\)

Theo định nghĩa về giới hạn tại 1 điểm: giới hạn tại 1 điểm chỉ tồn tại khi giới hạn trái và giới hạn phải tại đó bằng nhau.

Nghĩa là muốn \(\lim\limits_{x\rightarrow a}f\left(x\right)\) thì \(\lim\limits_{x\rightarrow a^+}f\left(x\right)=\lim\limits_{x\rightarrow a^-}f\left(x\right)\)

Trong ví dụ của em \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=-\infty\) còn \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=+\infty\)

Rõ ràng là \(-\infty\ne+\infty\) nên \(\lim\limits_{x\rightarrow2}\dfrac{3x^2+x-1}{2x^2-5x+2}\) ko tồn tại

\(a+\dfrac{x+1}{\sqrt{x^2-x+1}}-\dfrac{3x+3}{\sqrt{x}}=0\) có nghiệm \(x=1\)

\(\Rightarrow a+\dfrac{2}{\sqrt{1}}-\dfrac{6}{\sqrt{1}}=0\Rightarrow a=4\)

\(4+\dfrac{x+1}{\sqrt{x^2-x+1}}-\dfrac{3x+3}{\sqrt{x}}=3\left(2-\dfrac{x+1}{\sqrt{x}}\right)+\left(\dfrac{x+1}{\sqrt{x^2-x+1}}-2\right)\)

\(=-3\left(\dfrac{\left(x-1\right)^2}{\sqrt{x}\left(x+1+2\sqrt{x}\right)}\right)+\dfrac{-3\left(x-1\right)^2}{\sqrt{x^2-x+1}\left(x+1-2\sqrt{x^2-x+1}\right)}\)

Rút gọn với \(\left(x-1\right)^2\) bên ngoài rồi thay dố là được

Dạng \(u_{n+1}=\dfrac{au_n+b}{cu_n+d}\) này có 1 cách làm chung:

Đặt \(v_n=u_n+k\) với k sao cho sau khi chuyển vế rút gọn thì tử số của \(\dfrac{au_n+b}{cu_n+d}\) triệt tiêu mất số hạng tự do b là được.

Ví dụ ở bài này, ta đặt ra nháp:

\(u_n=v_n+k\Rightarrow v_{n+1}+k=\dfrac{4\left(v_n+k\right)+2}{v_n+3+k}\)

\(\Rightarrow v_{n+1}=\dfrac{4v_n+4k+2}{v_n+k+3}-k=\dfrac{4v_n+4k+2-k\left(v_n+k+3\right)}{v_n+k+3}\)

\(=\dfrac{\left(4-k\right)v_n+2-k^2+k}{v_n+k+3}\)

Cần k sao cho \(-k^2+k+2=0\Rightarrow k=-1\) (lấy số nhỏ cho gọn). Vậy là xong. Thực tế ta làm như sau:

Đặt \(u_n=v_n-1\Rightarrow v_1=u_1+1=4\)

\(v_{n+1}-1=\dfrac{4\left(v_n-1\right)+2}{v_n+2}\Rightarrow v_{n+1}=\dfrac{4v_n-2}{v_n+2}+1=\dfrac{5v_n}{v_n+2}\)

(sau đó nghịch đảo 2 vế):

\(\Rightarrow\dfrac{1}{v_{n+1}}=\dfrac{v_n+2}{5v_n}=\dfrac{2}{5}.\dfrac{1}{v_n}+\dfrac{1}{5}\)

(Đây là gần như 1 dãy bình thường rồi)

(Tiếp tục đặt \(\dfrac{1}{v_n}=x_n+k\) sao cho triệt tiêu nốt số hạng \(\dfrac{1}{5}\) bên phải đi:

\(x_{n+1}+k=\dfrac{2}{5}\left(x_n+k\right)+\dfrac{1}{5}\Rightarrow x_{n+1}=\dfrac{2}{5}.x_n+\dfrac{2k}{5}+\dfrac{1}{5}-k\)

\(\Rightarrow\dfrac{2k}{5}+\dfrac{1}{5}-k=0\Rightarrow k=\dfrac{1}{3}\))

Đặt \(\dfrac{1}{v_n}=x_n+\dfrac{1}{3}\Rightarrow x_1=\dfrac{1}{v_1}-\dfrac{1}{3}=\dfrac{1}{4}-\dfrac{1}{3}=-\dfrac{1}{12}\)

\(\Rightarrow x_{n+1}+\dfrac{1}{3}=\dfrac{2}{5}\left(x_n+\dfrac{1}{3}\right)+\dfrac{1}{5}\Leftrightarrow x_{n+1}=\dfrac{2}{5}x_n\)

Đây là công thức cấp số nhân dạng , do đó ta có: \(x_n=-\dfrac{1}{12}.\left(\dfrac{2}{5}\right)^{n-1}\)

\(\Rightarrow\dfrac{1}{v_n}=x_n+\dfrac{1}{3}=-\dfrac{1}{12}.\left(\dfrac{2}{5}\right)^{n-1}+\dfrac{1}{3}=-\dfrac{2^{n-1}}{12.5^{n-1}}+\dfrac{4.5^{n-1}}{12}=\dfrac{4.5^{n-1}-2^{n-1}}{12.5^{n-1}}\)

\(\Rightarrow v_n=\dfrac{12.5^{n-1}}{4.5^{n-1}-2^{n-1}}\)

\(\Rightarrow u_n=v_n-1=\dfrac{12.5^{n-1}}{4.5^{n-1}-2^{n-1}}-1\)

\(lim\left(u_n+4\right)=lim\left(\dfrac{12.5^{n-1}}{4.5^{n-1}-2^{n-1}}+3\right)=\dfrac{12}{4}+3=6\)

Đây là cách làm cơ bản, còn trên thực tế, khi trắc nghiệm chỉ cần đơn giản như sau:

Giả sử \(lim\left(u_n\right)=a\), hiển nhiên dãy đã cho dương nên a dương

Lấy giới hạn 2 vế giả thiết:

\(lim\left(u_{n+1}\right)=lim\left(\dfrac{4u_n+2}{u_n+3}\right)\Rightarrow a=\dfrac{4a+2}{a+3}\)

\(\Rightarrow a^2+3a=4a+2\)

\(\Rightarrow a^2-a-2=0\Rightarrow\left[{}\begin{matrix}a=-1\\a=2\end{matrix}\right.\) \(\Rightarrow a=2\)

\(\Rightarrow lim\left(u_n+4\right)=2+4=6\)

Nhanh hơn khoảng 1 tỉ lần :D