Trình bày cách giải mấy câu này giúp mình với ạ :((( khó quá


#chuyên mục chữa đề
mong mọi người trình bày cách giải của mấy câu sai giúp em ạ :((( đề khó quá


11.
\(tan\left(x-\pi\right)=-tan\left(\pi-x\right)=tanx\)
12.
\(sinx+sin3x=2sin\dfrac{x+3x}{2}.cos\dfrac{x-3x}{2}=2sin2x.cos\left(-x\right)=2sin2x.cosx\)
15.
\(x^2+y^2-2x+4y-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=9\)
\(\Rightarrow\) Tâm \(I=\left(1;-2\right)\), bán kính \(R=3\)
Mọi người trình bày cách giải mấy câu này giúp em với ạ!!

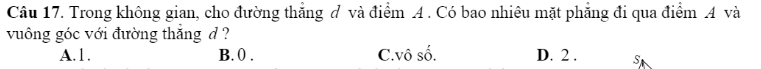
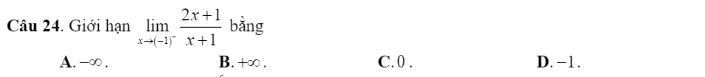

2.B (t/c của giới hạn)
6.B H/s ko x/đ với x = 0 -> Ko liên tục tại đ x = 0
17.C
24. \(\lim\limits_{x\rightarrow\left(-1\right)^-}\dfrac{2x+1}{x+1}\) . Thấy : \(\lim\limits_{x\rightarrow\left(-1\right)^-}2x+1=2.\left(-1\right)+1=-1\)
\(\lim\limits_{x\rightarrow\left(-1\right)^-}x+1=0\) ; \(x\rightarrow\left(-1\right)^-\Rightarrow x+1< 0\).
Do đó : \(\lim\limits_{x\rightarrow\left(-1\right)^-}=+\infty\) . Chọn B
33 . B
Trên (SAB) ; Lấy H là TĐ của AB ; ta có : SH \(\perp AB\) ( \(\Delta SAB\) đều ) ; HC \(\perp AB\) ( \(\Delta ABC\) đều )
Ta có : (SAB) \(\perp\left(ABC\right)\) ; \(\left(SAB\right)\cap\left(ABC\right)=AB;SH\perp AB\)
\(\Rightarrow SH\perp\left(ABC\right)\)
\(SC\cap\left(ABC\right)=C\) . Suy ra : \(\left(SC;\left(ABC\right)\right)=\widehat{SCH}\)
Có : \(SH\perp HC\) => \(\Delta SHC\) vuông tại H
G/s \(\Delta\)ABC đều có cạnh là a \(\Rightarrow AB=a\)
\(\Delta SAB\) đều => SA = SB = AB = a
Tính được : \(SH=HC=\dfrac{\sqrt{3}}{2}a\)
\(\Delta SHC\) vuông tại H : \(tan\widehat{SCH}=\dfrac{SH}{HC}=1\)
\(\Rightarrow\widehat{SCH}=45^o\) => ...

trình bày cách giải của từng câu giúp mình với ạ :((( chứ chọn đáp án thôi thì khó hiểu lắm
7.
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-1;2\right)\\\overrightarrow{AC}=\left(-1;1\right)\end{matrix}\right.\)
\(cosA=\dfrac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}=\dfrac{\left(-1\right).\left(-1\right)+2.1}{\sqrt{1^2+2^2}.\sqrt{1^2+1^2}}=\dfrac{3}{\sqrt{10}}\)
Thật kì diệu là cả 4 đáp án đều sai :D
8.
\(\left\{{}\begin{matrix}\overrightarrow{AC}=\left(x_0-2;-1\right)\\\overrightarrow{AB}=\left(1;0\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AC^2=\left(x_0-2\right)^2+1\\AB^2=1\end{matrix}\right.\)
\(\Rightarrow\left(x_0-2\right)^2+1=4\Rightarrow\left(x_0-2\right)^2=3\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2-\sqrt{3}\\x_0=2+\sqrt{3}\end{matrix}\right.\)
Lại 1 câu rất ảo nữa, có tới 2 giá trị thỏa mãn, nhưng bạn có thể chọn A (ứng với trường hợp thứ nhất)
Trình bày lời giải mấy câu này giúp em với ạ

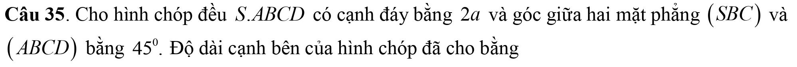
34:
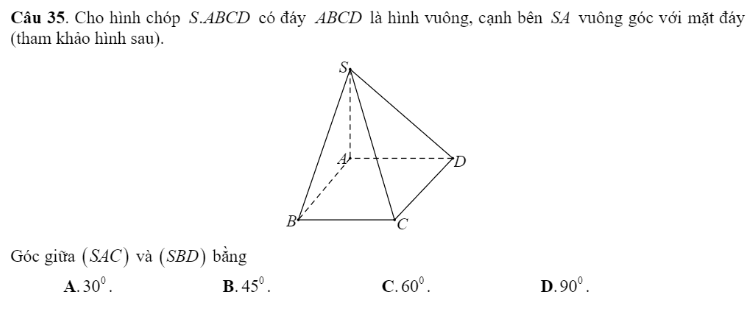
(SBA) giao (SCD)=d đi qua S, d//AB//CD
=>d vuông góc SA,d vuông góc SD
=>(SAB;SCD)=(SA;SD)
tan ASD=AD/AS=1/căn 3
=>góc ASD=30 độ
lần này không phải chữa đề mà là giải đề ạ :(( mấy câu cuối của đề toán lúc nào cũng là vấn đề đối với mấy đứa tệ toán như em . Mong mọi người giúp đỡ và trình bày cách giải ạ

17.
\(f\left(x\right)>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\left(luôn-đúng\right)\\\Delta'=\left(2m-1\right)^2-\left(3m^2-2m+4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow m^2-2m-3< 0\)
\(\Leftrightarrow-1< m< 3\)
\(\Rightarrow m=\left\{0;1;2\right\}\)
18.
\(\pi< x< \dfrac{3\pi}{2}\Rightarrow cosx< 0\)
\(\Rightarrow cosx=-\sqrt{1-sin^2x}=-\dfrac{\sqrt{5}}{3}\)
\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\dfrac{2\sqrt{5}}{5}\)
\(tan\left(x+\dfrac{\pi}{4}\right)=\dfrac{tanx+tan\dfrac{\pi}{4}}{1-tanx.tan\dfrac{\pi}{4}}=\dfrac{\dfrac{2\sqrt{5}}{5}+1}{1-\dfrac{2\sqrt{5}}{5}.1}=9+4\sqrt{5}\)
19.
\(a^2=b^2+c^2+bc\Rightarrow b^2+c^2-a^2=-bc\)
\(\Rightarrow cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{-bc}{2bc}=-\dfrac{1}{2}\)
\(\Rightarrow A=120^0\)
20.
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\)
\(d\left(I;\Delta\right)=\dfrac{\left|2-1-3\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}IH=d\left(I;\Delta\right)\\AH=\dfrac{1}{2}AB\end{matrix}\right.\)
Áp dụng định lý Pitago trong tam giác vuông IAH:
\(IA^2=IH^2+AH^2\Leftrightarrow R^2=IH^2+AH^2\)
\(\Rightarrow AH=\sqrt{2}\Rightarrow AB=2AH=2\sqrt{2}\)
21.
\(2x^2-\left(m+1\right)x+3m-15\le0\)
\(\Leftrightarrow2x^2-x-15-m\left(x-3\right)\le0\)
\(\Leftrightarrow\left(x-3\right)\left(2x+5\right)-m\left(x-3\right)\le0\)
\(\Leftrightarrow\left(x-3\right)\left(2x+5-m\right)\le0\)
Do \(x\in\left[1;2\right]\Rightarrow x-3< 0\) nên BPT tương đương:
\(2x+5-m\ge0\)
\(\Leftrightarrow2x+5\ge m\)
BPT đúng với mọi \(x\in\left[1;2\right]\) khi và chỉ khi: \(m\le7\)
\(\Rightarrow m=\left\{1;2;3;4;5;6;7\right\}\)
Cả 4 đáp án đều sai?
P/s: đã thử lại, chỉ có 7 giá trị nguyên dương là đáp án đúng
Trình bày lời giải mấy câu này giúp em với ạ!! Em xin cảm ơn.
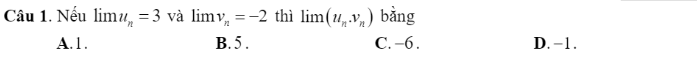



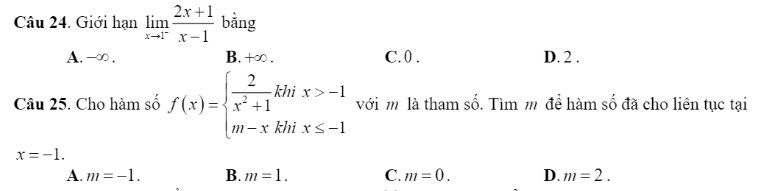

Bạn nào giải giúp mình hai câu này vs ạ , trình bày hộ mình với , mình cám ơn ạ
22/ \(\omega A=8\pi\)
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Leftrightarrow A^2=3,2^2+\dfrac{\left(4,8\pi\right)^2}{\omega^2}\)
\(\Leftrightarrow\omega^2A^2=3,2^2\omega^2+23,04\pi^2\Leftrightarrow64\pi^2=3,2^2.\omega^2+23,04\pi^2\Leftrightarrow\omega=2\pi\left(rad/s\right)\)
\(\Rightarrow f=\dfrac{\omega}{2\pi}=\dfrac{2\pi}{2\pi}=1\left(Hz\right)\Rightarrow D.1Hz\)
23/ \(\omega A=20;\omega^2A=80\Rightarrow\left\{{}\begin{matrix}\omega=4\left(rad/s\right)\\A=5cm\end{matrix}\right.\)
\(\Rightarrow v=\omega\sqrt{A^2-x^2}=4.\sqrt{5^2-4^2}=12\left(cm/s\right)\Rightarrow A.12cm/s\)
#chuyên mục chữa đề
Vẫn là mong được giúp đỡ, câu sai (và mấy câu chưa làm được) thì trình bày cách giải giúp em với ạ


Tính giá trị của biểu thức
A) (-125).(-13).(-a), với a=8
b) (-1).(-2).(-3).(-4).(-5).b, với b=20
Bài này mình bí quá trời luôn, mong mấy bạn giải giúp, mình sẽ like cho, trình bày cách giải mình like thêm nha!