Trong mặt phẳng toạ độ Oxy, cho đường thẳng d: mx + y - m + 4 = 0 và điểm A(2;1). Tính tổng tất cả các giá trị tham số m để khoảng cách từ A đến d bằng \(\sqrt{5}\)
LH
Những câu hỏi liên quan
1. Trong mặt phẳng toạ độ oxy, cho 2 đường thẳng delta :x+2y+40 và d: 2x-y+30. Đường tròn tâm I thuộc d cắt Ox tại A và B, cắt trục Oy tại C và D sao cho ABCD2. Tính khoảng cách từ điểm I đến đường thăng delta2. trong mặt phẳng toạ độ oxy, cho tứ giác ABCD với AB:3x-4y+40, BC: 5+12y-520, CD: 5x-12y-40, AD:3x+4y-120. tìm điểm I nằm trong tứ giác ABCD sao cho d(I, AB)d(I,BC)d(I,CD)d(I,DA)
Đọc tiếp
1. Trong mặt phẳng toạ độ oxy, cho 2 đường thẳng delta :x+2y+4=0 và d: 2x-y+3=0. Đường tròn tâm I thuộc d cắt Ox tại A và B, cắt trục Oy tại C và D sao cho AB=CD=2. Tính khoảng cách từ điểm I đến đường thăng delta
2. trong mặt phẳng toạ độ oxy, cho tứ giác ABCD với AB:3x-4y+4=0, BC: 5+12y-52=0, CD: 5x-12y-4=0, AD:3x+4y-12=0. tìm điểm I nằm trong tứ giác ABCD sao cho d(I, AB)=d(I,BC)=d(I,CD)=d(I,DA)
Trong mặt phẳng toạ độ Oxy cho đường thẳng (d): y=\(-mx-m+3\) và (P): y=\(2x^2\)
a,Tìm toạ độ giao điểm của (d) và (P) khi m=5
Khi \(m=5\) pt (d) có dạng: \(y=-5x-2\)
Phương trình hoành độ giao điểm (d) và (P):
\(2x^2=-5x-2\Leftrightarrow2x^2+5x+2=0\Rightarrow\left[{}\begin{matrix}x=-\frac{1}{2}\\x=-2\end{matrix}\right.\)
Với \(x=-\frac{1}{2}\Rightarrow y=2x^2=\frac{1}{2}\)
Với \(x=-2\Rightarrow y=2x^2=8\)
Vậy có 2 giao điểm: \(\left(-\frac{1}{2};\frac{1}{2}\right)\) và \(\left(-2;8\right)\)
Đúng 0
Bình luận (0)
1. Trong mặt phẳng với hệ toạ độ Oxy, viết phương trình đường thẳng △ song song với đường thẳng d: 2x-y+2015=0 và cắt hai trục toạ độ tại M và N sao cho MN=3√5
2.Trong mặt phẳng với hệ toạ độ Oxy, cho 2 điểm A(1;2) ; B(4;3). Tìm toạ độ điểm M sao cho ∠MAB=135 độ và khoảng cách từ M đến đường thẳng AB bằng √10/2
Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho parabol (P) y=x^2 và đường thẳng (d) y=x+2.
a) vẽ parabol (P) và đường thẳng (d) trên cùng mặt phẳng toạ độ Oxy.
b) Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.
c) viết phương trình đường thẳng (d') có dạng y=ax+b , biết (d') song song với (d) và đi qua điểm M(2:5)
`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
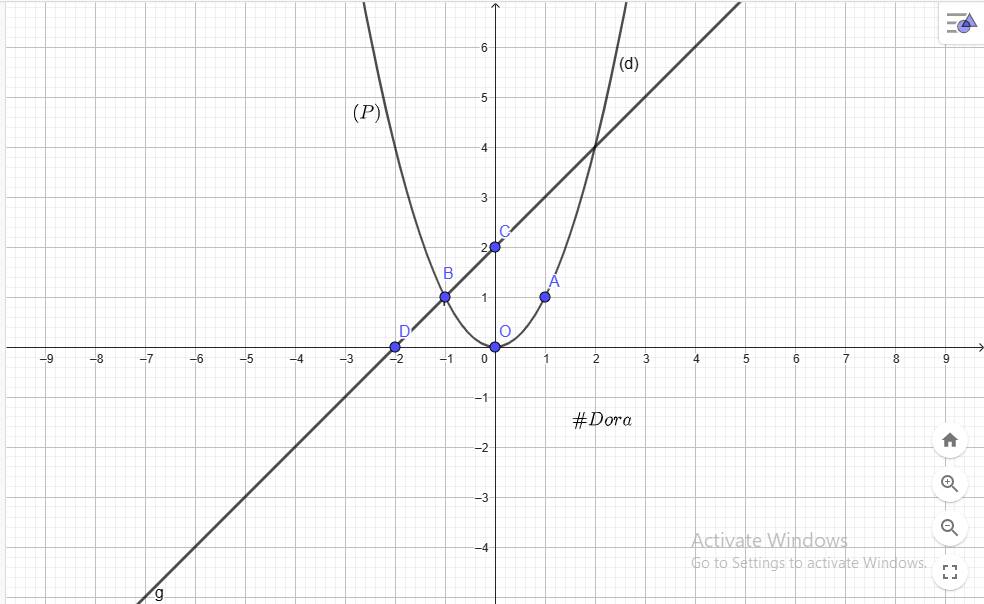
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`
Đúng 4
Bình luận (0)
trong mặt phẳng toạ độ Oxy cho parabol y=3/2x^2 và đường thẳng (d) y=mx+4 a) vẽ đồ thị (P) b) Tìm tất cả giá trị của m để (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1 , x2 thoả mãn x1^2+x2^2-x1x2 =24
b: Phương trình hoành độ giao điểm là:
\(\dfrac{3}{2}x^2-mx-4=0\)
\(\Leftrightarrow3x^2-2mx-8=0\)
ac<0 nên (P) luôn cắt (d) tại hai điểm phân biệt
Theo đề, ta có: \(\left(x_1+x_2\right)^2-3x_1x_2=24\)
\(\Leftrightarrow m^2\cdot\dfrac{4}{9}-3\cdot\dfrac{-8}{3}=24\)
\(\Leftrightarrow m^2\cdot\dfrac{4}{9}=16\)
hay m=6 hoặc m=-6
Đúng 3
Bình luận (1)
Trong mặt phẳng toạ độ Oxy, cho đường thẳng (d): y = 2mx - m2 + 1 và parabol (P): y = x2
a) Tìm toạ độ hai giao điểm của (d) và (P) khi m = 2.
b) Tìm m để đường thẳng (d) cắt (P) tại 2 điểm có hoành độ x1, x2 thoả mãn: 2y1 + 4mx2 - 2m2 - 3 < 0
a: khi m=2 thì (d): y=4x-2^2+1=4x-3
PTHĐGĐ:
x^2-4x+3=0
=>x=1 hoặc x=3
Khi x=1 thì y=1
Khi x=3 thì y=9
b: PTHĐGĐ là;
x^2-2mx+m^2-1=0
Δ=(-2m)^2-4(m^2-1)=4>0
=>(P) luôn cắt (d) tại hai điểm phân biệt
2y1+4m*x2-2m^2-3<0
=>2(2mx1-m^2+1)+4m*x2-2m^2-3<0
=>4m*x1-2m^2+2+4m*x2-2m^2-3<0
=>-4m^2+4m*(x1+x2)-1<0
=>-4m^2+4m*(2m)-1<0
=>-4m^2+8m-1<0
=>\(\left[{}\begin{matrix}m< \dfrac{2-\sqrt{3}}{2}\\m>\dfrac{2+\sqrt{3}}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy,Oxy, cho đường thẳng (d):y2mx−m2+1(d):y2mx−m2+1 và parabol (P):yx2.
a)Tìm toạ độ hai giao điểm của P và d khi m2
b)Tìm m để đường thẳng d cắt p tại 2 điểm có hoành độ x1,x2 thoả mãn:
2y1+4mx2-2x^2-30
(P):yx2.
Đọc tiếp
Trong mặt phẳng tọa độ cho đường thẳng và parabol
b)Tìm m để đường thẳng d cắt p tại 2 điểm có hoành độ x1,x2 thoả mãn:
2y1+4mx2-2x^2-3<0
Trong mặt phẳng Oxy,cho đường thẳng d:x-2y+1=0 và điểm M(2;-2).Toạ độ hình chiếu vuông góc của điểm M lên đường thẳng d là
Phương trình đường vuông góc kẻ từ M đến d là \(2x+y-6=0\)
Hình chiếu của M trên d có tọa độ là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-2y+1=0\\2x+y-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{5}\\y=\dfrac{8}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (3)
Phương trình đường thẳng vuông góc kẻ từ M đến d là \(2x+y-2=0\)
Hình chiếu của M có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}x-2y+1=0\\2x+y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=\dfrac{4}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho A(2;2). Tìm toạ độ điểm B trên đường thẳng (d): y = 2 – x và toạ độ điểm C trên đường thẳng (d’): y = 8 – x sao cho tam giác ABC vuông cân tại A
Ta có B(a;2-a) ; C(b;8-b)
Để tam giác ABC vuông cân tại A
\(\left\{{}\begin{matrix}\overrightarrow{AC}.\overrightarrow{AB}=\overrightarrow{0}\\\overrightarrow{AC}=\overrightarrow{AB}\end{matrix}\right.\) bạn thay vào giải hpt bằng p2 thế nhé
Đúng 1
Bình luận (1)



