Bài 2: Đồ thị hàm số y = ax^2 (a khác 0)
a: Xét (O) có
MA,MC là các tiếp tuyến
Do đó: MA=MC
=>M nằm trên đường trung trực của AC(1)
Ta có: OA=OC
=>O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra MO là đường trung trực của AC
=>MO\(\perp\)AC tại E và E là trung điểm của AC
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)MB tại D
Xét ΔMAB vuông tại A có AD là đường cao
nên \(MD\cdot MB=MA^2\)
mà MA=MC
nên \(MD\cdot MB=MC^2\)
b: Xét tứ giác AEDM có \(\widehat{AEM}=\widehat{ADM}=90^0\)
nên AEDM là tứ giác nội tiếp
c: Gọi giao điểm của BC với AM là K
Ta có: CH\(\perp\)AB
AM\(\perp\)AB
Do đó: CH//AM
Ta có: \(\widehat{MCA}+\widehat{MCK}=\widehat{ACK}=90^0\)
\(\widehat{MAC}+\widehat{MKC}=90^0\)(ΔCKA vuông tại C)
mà \(\widehat{MAC}=\widehat{MCA}\)(ΔMAC cân tại M)
nên \(\widehat{MCK}=\widehat{MKC}\)
=>MK=MC
mà MA=MC
nên MK=MA(3)
Xét ΔBMK có CF//MK
nên \(\dfrac{CF}{MK}=\dfrac{BF}{BM}\left(4\right)\)
Xét ΔBAM có HF//AM
nên \(\dfrac{HF}{AM}=\dfrac{BF}{BM}\left(5\right)\)
Từ (3),(4),(5) suy ra CF=HF
=>F là trung điểm của CH
Xét ΔCAH có
E,F lần lượt là trung điểm của CA,CH
=>EF là đường trung bình của ΔCAH
=>EF//AH
=>EF//AB
Đúng 1
Bình luận (0)
. Xét vị trí tương đối của hai trong bốn đường thẳng sau
(d): y=3x+1; (d): y=-√3x+2
(d): y=3x+2 (d): y = √3x+2
Vì 3=3 và 1<>2
nên hai đường thẳng y=3x+1 song song với y=3x+2
Vì \(3\ne\sqrt{3}\) nên hai đường thẳng y=3x+1 và \(y=\sqrt{3}x+2\) cắt nhau
Vì \(3\ne\sqrt{3}\) nên hai đường thẳng y=3x+2 và \(y=\sqrt{3}x+2\) cắt nhau
Vì \(3\ne-\sqrt{3}\)
nên hai đường thẳng y=3x+1 và \(y=-\sqrt{3}x+2\) cắt nhau
Vì \(3\ne-\sqrt{3}\) và 2=2
nên hai đường thẳng y=3x+2 và \(y=-\sqrt{3}x+2\) cắt nhau tại một điểm trên trục tung
Đúng 3
Bình luận (0)
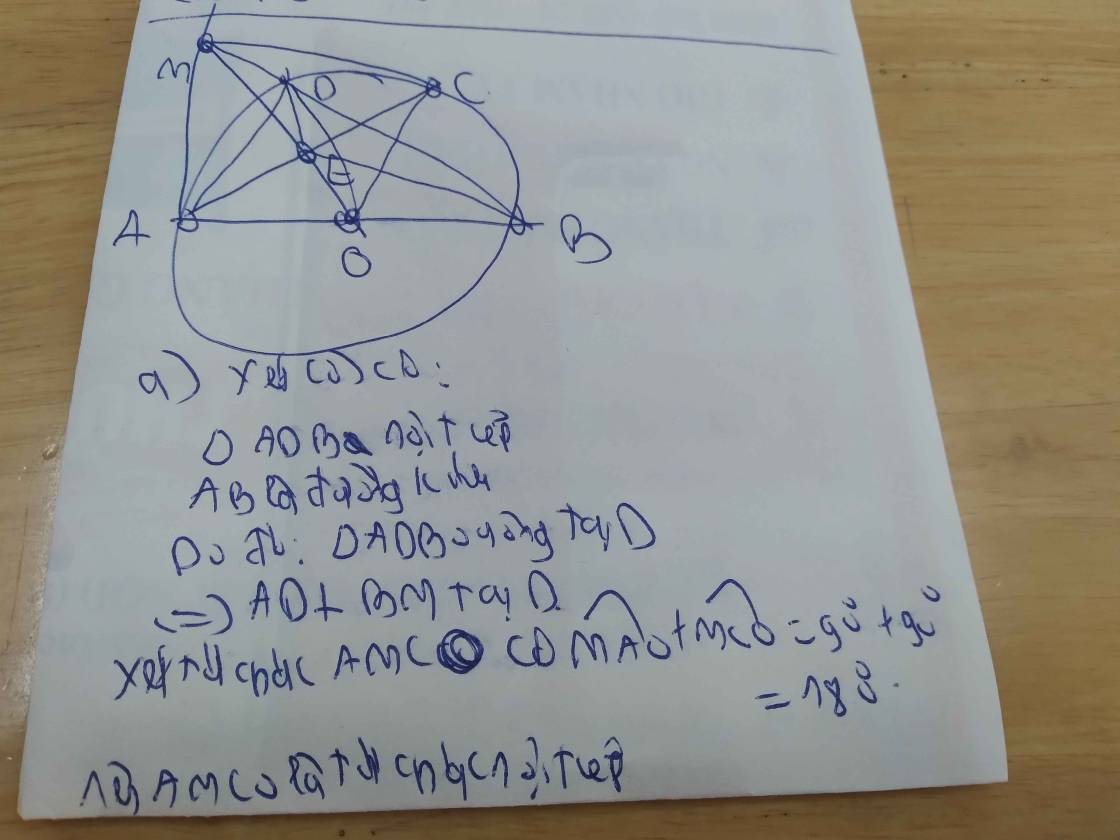
AB, kẻ cho nửa đường tròn tâm O đường kính AB. Trên nửa mặt phẳng chứa nửa đường tròn đường kính AB, kẻ Ax vuông góc với AB. Từ điểm M trên tia Ax kẻ tiếp tuyến MC ( C là tiếp điểm khác A). Đoạn thẳng AC cắt OM tại E, MB cắt nửa đường tròn tại D (D khác B).
a) Chứng minh AMCO và AMDE là các tứ giác nội tiếp được đường tròn. c)
Chứng minh MOD MBE
d) Gọi H là hình chiếu vuông góc của C lên AB là giao điểm của MB và CH. Chúng mình rằng El
b) Chứng minh MC² MB.MD d)
Đọc tiếp
AB, kẻ cho nửa đường tròn tâm O đường kính AB. Trên nửa mặt phẳng chứa nửa đường tròn đường kính AB, kẻ Ax vuông góc với AB. Từ điểm M trên tia Ax kẻ tiếp tuyến MC ( C là tiếp điểm khác A). Đoạn thẳng AC cắt OM tại E, MB cắt nửa đường tròn tại D (D khác B). a) Chứng minh AMCO và AMDE là các tứ giác nội tiếp được đường tròn. c) Chứng minh MOD = MBE d) Gọi H là hình chiếu vuông góc của C lên AB là giao điểm của MB và CH. Chúng mình rằng El b) Chứng minh MC² = MB.MD d)
2)Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = x và đường thẳng (d): y = 2x+ 3 a. Tìm tọa độ các giao điểm của (đ) và (P). b. Gọi A, B là giao điểm của (d) và (P). Tính diện tích tam giác OAB.
Cho hàm số y = f(x) = \(ax^2\). Biết rằng điểm A(1; 2) thuộc đồ thị của hàm số.
a) Xác định hàm số a.
b) Vẽ đồ thị
a: Thay x=1 và y=2 vào \(y=f\left(x\right)=ax^2\), ta được:
\(a\cdot1^2=2\)
=>a*1=2
=>a=2
=>\(y=2x^2\)
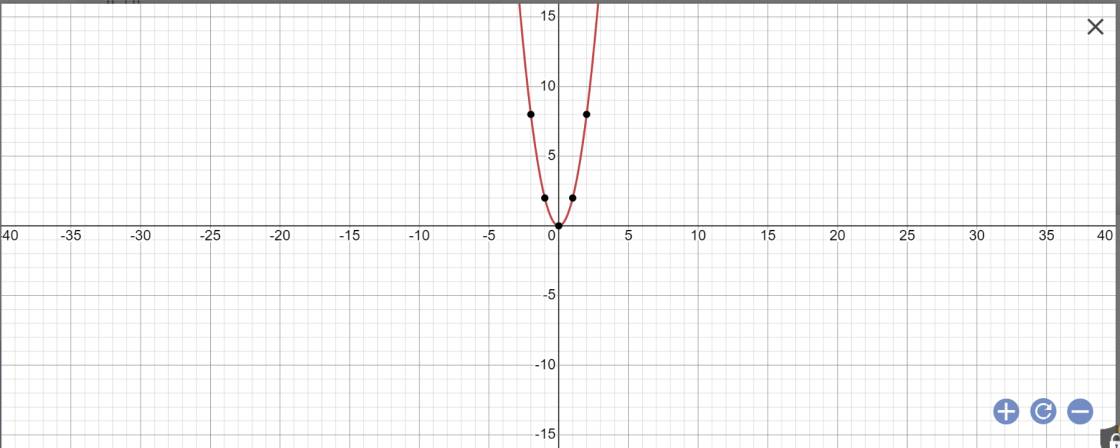
b: bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| \(y=2x^2\) | 8 | 2 | 0 | 2 | 8 |
Đồ thị:
Đúng 2
Bình luận (0)
tìm k để y = x^2 cắt đường thẳng y=30x+k tại 2 điểm có hoành độ là số nguyên tố
PTHĐGĐ là:
x^2-30x-k=0
Δ=(-30)^2-4*1*(-k)=4k+900
Để phương trình có hai nghiệm thì 4k+900>=0
=>k>=-225
x1+x2=30
mà x1,x2 nguyên tố
nên x1=7; x2=23
x1*x2=-k
=>-k=23*7=161
=>k=-161(nhận)
Đúng 0
Bình luận (0)
tìm k để y=^2 cắt y=30x+k tại 2 điểm có hoành độ là các số nguyên tố
(P) y = –x² và đt (d) y = mx + 2 ( m là tham số ) tìm m để (P) tiếp xúc (d)
PTHĐGĐ là:
-x^2-mx-2=0
=>x^2+mx+2=0
Δ=m^2-4*1*2=m^2-8
Để (P) tiếp xúc (d) thì m^2-8=0
=>\(m=\pm2\sqrt{2}\)
Đúng 1
Bình luận (0)
1) Vẽ đồ thị hàm số y=1/2 x² 2) Xác định giá trị của m để đường thẳng y=x+m cắt Parabol (P) tại 2 điểm phân biệt
Cho hàm số y= 1/4x^2 có đồ thị là (P)
a) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy
b) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 100
a) Bảng giá trị:

Đồ thị:
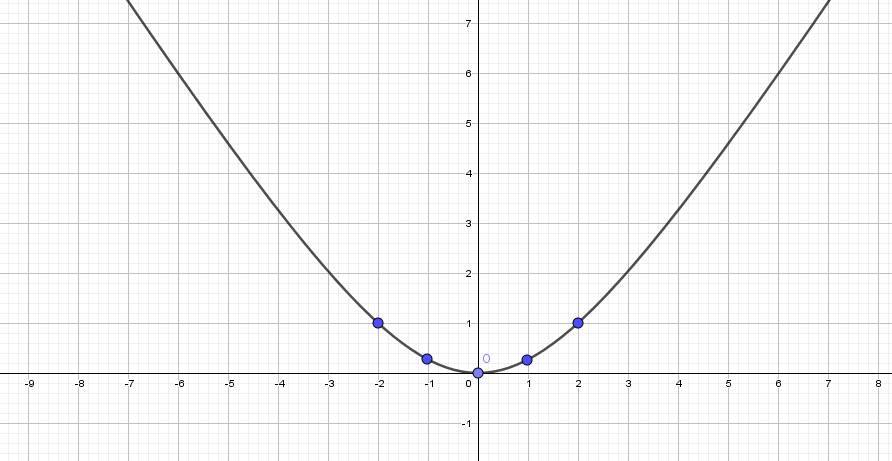
b) Thay y = 100 vào (P) ta được:
\(\dfrac{1}{4}x^2=100\)
\(\Leftrightarrow x^2=100:\dfrac{1}{4}\)
\(\Leftrightarrow x^2=400\)
\(\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-20\end{matrix}\right.\)
Vậy M(-20; 100) hoặc M(20; 100)
Đúng 1
Bình luận (0)
b: y=100
=>1/4x^2=100
=>x^2=400
=>x=20 hoặc x=-20
a: 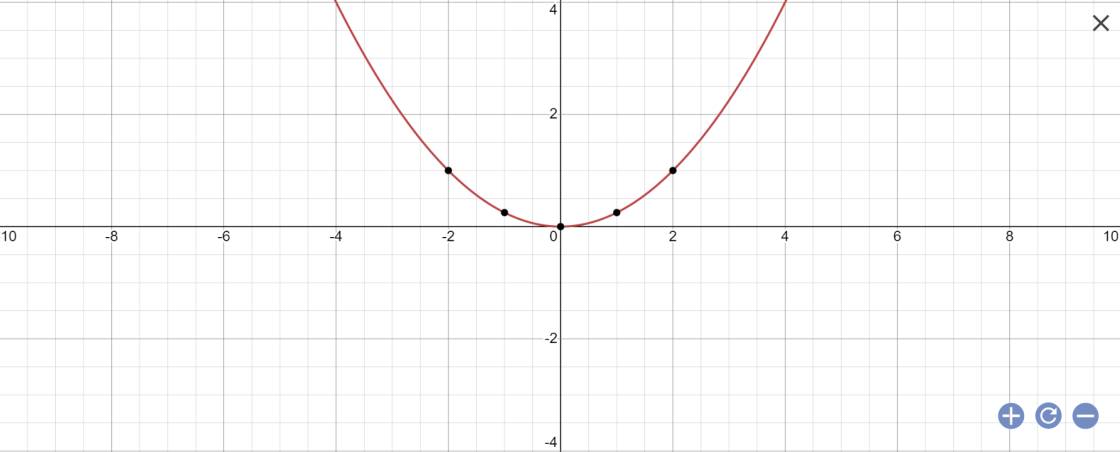
Đúng 0
Bình luận (0)