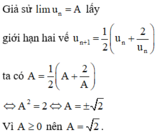cho dãy sô Un được xác định U1=1\(\dfrac{1}{2}\); U2=2\(\dfrac{1}{3}\)
Un+2=3Un+1-2Un với n \(\in\)N tính U25
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TA
Những câu hỏi liên quan
1) cho dãy số (un)(��) được xác định bởi unn^2-1�3�−1a) Tính u1,u2,u3,u4b) 99 là số hạng thứ mấy của dãy2) cho dãy số (un)(��) được xác định bởi u_ndfrac{2n-1}{n+1}a) Tính u1,u2,u3,u4b) dfrac{13}{7} là số hạng thứ mấy của dãy
Đọc tiếp
1) cho dãy số được xác định bởi
a) Tính
2) cho dãy số được xác định bởi
b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
Đúng 0
Bình luận (0)
NH
19 tháng 1 2021 lúc 20:49
Cho dãy số (Un) được xác định bởi: u1 dfrac{1}{3} và un+1 dfrac{2u_n}{2u_nleft(3n-1right)+1}, ∀n ∈ N*.a) Tìm u4 và số hạng tổng quát un của dãy số.b) Tính S dfrac{1}{u_1}+dfrac{1}{u_2}+...+dfrac{1}{u_n} (tổng gồm n số hạng) theo n.Help me!!!Gấp lắm ạThank you so much!!!
Đọc tiếp
Cho dãy số (Un) được xác định bởi: u1 = \(\dfrac{1}{3}\) và un+1 = \(\dfrac{2u_n}{2u_n\left(3n-1\right)+1}\), ∀n ∈ N*.
a) Tìm u4 và số hạng tổng quát un của dãy số.
b) Tính S = \(\dfrac{1}{u_1}+\dfrac{1}{u_2}+...+\dfrac{1}{u_n}\) (tổng gồm n số hạng) theo n.
Help me!!!
Gấp lắm ạ
Thank you so much!!!
MN
28 tháng 3 2021 lúc 20:40
Cho dãy số (un) được xác định như sau: u1= 2017; un-1= n2(un-1 - un) với mọi n ∈ N*, n ≥2. Tìm giới hạn dãy số (un)
Lời giải:
$\frac{u_{n-1}}{u_n}=\frac{n^2}{n^2-1}>0$ với mọi $n\geq 2$ nên $u_{n-1}, u_n$ luôn cùng dấu.
Mà $u_1=2017>0$ nên $u_n>0$ với mọi $n=1,2,...$
Mặt khác:
$n^2(u_{n-1}-u_n)=u_{n-1}>0\Rightarrow u_{n-1}>u_n$ nên dãy $(u_n)$ là dãy giảm.
Dãy giảm và bị chặn dưới nên $u_n$ hội tụ. Đặt $\lim u_n=a$.
Ta có: $a=n^2(a-a)\Rightarrow a=0$
Vậy $\lim u_n=0$
Đúng 0
Bình luận (0)
cho dãy số un xác định bởi \(\left\{{}\begin{matrix}u1=2\\u_{n+1}=un+3\end{matrix}\right.\)với n\(\ge1\) Tính I=lim \(\dfrac{un}{3n+1}\)
Từ công thức dãy số ta thấy \(u_n\) là cấp số cộng với \(\left\{{}\begin{matrix}u_1=2\\d=3\end{matrix}\right.\)
\(\Rightarrow u_n=u_1+\left(n-1\right)d=2+\left(n-1\right)3=3n-1\)
\(\Rightarrow I=\lim\limits\dfrac{3n-1}{3n+1}=1\)
Đúng 1
Bình luận (0)
MN
29 tháng 3 2021 lúc 22:07
Cho dãy số (un), biết u1= 2, un+1= \(\dfrac{2017+u_n}{2019-u_n},n\ge1\) . Xác định công thức số hạng tổng quát un và tìm limun
Đặt \(u_n=v_n+1\Rightarrow v_{n+1}+1=\dfrac{2017+v_n+1}{2019-\left(v_n+1\right)}=\dfrac{2018+v_n}{2018-v_n}\)
\(\Rightarrow v_{n+1}=\dfrac{2018+v_n}{2018-v_n}-1=\dfrac{2v_n}{2018-v_n}\Rightarrow\dfrac{1}{v_{n+1}}=1009\dfrac{1}{v_n}-\dfrac{1}{2}\)
Đặt \(\dfrac{1}{v_n}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{1}{v_1}=\dfrac{1}{u_1-1}=1\\x_{n+1}=1009x_n-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow x_{n+1}-\dfrac{1}{2016}=1009\left(x_n-\dfrac{1}{2016}\right)\)
\(\Rightarrow x_n-\dfrac{1}{2016}\) là CSN với công bội 1009 \(\Rightarrow x_n-\dfrac{1}{2016}=\dfrac{2015}{2016}.1009^{n-1}\)
\(\Rightarrow x_n=\dfrac{2015}{2016}1009^{n-1}+\dfrac{1}{2016}\)
\(\Rightarrow u_n=v_n+1=\dfrac{1}{x_n}+1=\dfrac{2016}{2015.1009^{n-1}+1}+1\)
\(\Rightarrow\lim\left(u_n\right)=1\)
Đúng 2
Bình luận (3)
Cho dãy số (un) xác định bởi : u1=1 ,\(u_{n+1}=\dfrac{3}{2}\left(u_n-\dfrac{n+4}{n^2+3n+2}\right)\)
Tìm công thức số hạng tổng quát un theo n
\(u_{n+1}=\dfrac{3}{2}\left(u_n-\dfrac{n+4}{\left(n+1\right)\left(n+2\right)}\right)=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}+\dfrac{2}{n+2}\right)\)
\(\Leftrightarrow u_{n+1}-\dfrac{3}{n+1+1}=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}\right)\)
Đặt \(u_n-\dfrac{3}{n+1}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-\dfrac{3}{2}=-\dfrac{1}{2}\\v_{n+1}=\dfrac{3}{2}v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội \(\dfrac{3}{2}\)
\(\Rightarrow v_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}\)
\(\Rightarrow u_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}+\dfrac{3}{n+1}\)
Đúng 2
Bình luận (0)
Cho dãy số
u
n
được xác định bởi
u
1
2
u
n
+
1...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 2 u n + 1 = 4 u n + 9
Dãy số v n xác định bởi v n = u n + 3 , với mọi n ≥ 1 . Khẳng định nào dưới đây đúng?
A. Dãy v n là cấp số cộng với công sai d=3 .
B. Dãy v n là cấp số nhân với công bội q=4.
C. Dãy v n là cấp số cộng với công sai d=4 .
D. Dãy v n là cấp số nhân với công bội q= 9
Cho dãy số
u
n
được xác định bởi
u
1
1
;
u
n
+
1
1
2
u
n
+
2
u
n...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 1 ; u n + 1 = 1 2 u n + 2 u n với mọi n ≥ 1 . Tìm lim u n
A. 1
B. -1
C. 2
D. - 2
Cho dãy số (un) xác định bởi : u1=3 , \(u_{n+1}=\dfrac{2u_n+2}{3}\) Với mọi N thuộc N*
Tìm công thức số hạng tổng quát un theo n
\(u_{n+1}=\dfrac{2}{3}u_n+\dfrac{2}{3}\Rightarrow u_{n+1}-2=\dfrac{2}{3}\left(u_n-2\right)\)
Đặt \(u_n-2=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-2=1\\v_{n+1}=\dfrac{2}{3}v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội \(q=\dfrac{2}{3}\Rightarrow v_n=1.\left(\dfrac{2}{3}\right)^{n-1}=\left(\dfrac{2}{3}\right)^{n-1}\)
\(\Rightarrow u_n=v_n+2=\left(\dfrac{2}{3}\right)^{n-1}+2\)
Đúng 1
Bình luận (0)
Cho dãy số
u
n
được xác định bởi
u
1
1
,
u
n
+
1
1
2
u
n
+
2
u
n...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 1 , u n + 1 = 1 2 u n + 2 u n với mọi n ≥ 1 . Tìm giới hạn của u n
A. l i m u n = 1
B. l i m u n = - 1
C. l i m u n = 2
D. l i m u n = - 2
Chọn C.
Phương pháp : Dãy số giảm bị chặn dưới thì có giới hạn.
Cách giải : Dễ thấy dãy số đã cho là dãy số dương.
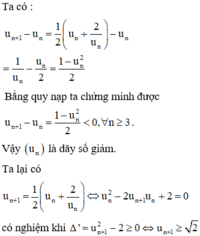
Vậy dãy số đã cho giảm và bị chặn dưới nên có giới hạn.
Đúng 0
Bình luận (0)