cho ba số nguyên theo thứ tự lập thành một cấp số nhân. Nếu tăng số hạng thứ hai thêm 9 đơn vị thì chúng lập thành cấp số cộng. Nếu tăng số hạng thứ hai thêm 2 đơn vị và số hạng thứ ba thêm 18 đơn vị thì chúng lập thành cấp số nhân. Tổng của ba số đó bằng
Bài 5: Ôn tập chương Dãy số. Cấp số cộng và cấp số nhân.
Khi nghiên cứu về một loại virus, người ta nhận thấy sau mỗi phút, số lượng virus tăng lên gấp 3 lần trước đó. Giả sử ban đầu từ 5 con virus, hãy tính số lượng virus có sau 11 phút.
Số lượng virus sau 11 phút là:
\(5\cdot3^{11}=885735\left(con\right)\)
Đúng 0
Bình luận (0)
1. Tìm \(x\) để 3 số \(\left\{{}\begin{matrix}a=x+1\\b=3x-2\\c=x^2-1\end{matrix}\right.\) lập thành cấp số cộng.
2. Tìm số hạng đầu, công sai, số hạng thứ 15 và tổng 15 số hạng đầu tiên của cấp số cộng với:
\(\left\{{}\begin{matrix}u_1+u_5-u_3=10\\u_1+u_6=17\end{matrix}\right.\)
Câu 2:
\(\left\{{}\begin{matrix}u_1+u_5-u_3=10\\u_1+u_6=17\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+u_1+4d-u_1-2d=10\\u_1+u_1+5d=17\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+2d=10\\2u_1+5d=17\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2u_1+4d=20\\2u_1+5d=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2u_1+4d-2u_1-5d=20-17\\2u_1+5d=17\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-d=3\\2u_1+5d=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=-3\\2u_1=17-5d=17+5\cdot3=32\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1=16\\d=-3\end{matrix}\right.\)
Câu 1:
Để a,b,c lập thành cấp số cộng thì
\(\left[{}\begin{matrix}a+c=2b\\a+b=2c\\b+c=2a\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x+1+x^2-1=2\cdot\left(3x-2\right)\\x+1+3x-2=2\left(x^2-1\right)\\x^2-1+3x-2=2\left(x+1\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x^2+x-6x+4=0\\2x^2-2=4x-1\\x^2+3x-3-2x-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x^2-5x+4=0\\2x^2-4x-1=0\\x^2+x-5=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(x-1\right)\left(x-4\right)=0\\2x^2-4x-1=0\\x^2+x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\in\left\{1;4\right\}\\x\in\left\{\dfrac{2+\sqrt{6}}{2};\dfrac{2-\sqrt{6}}{2}\right\}\\x\in\left\{\dfrac{-1+\sqrt{21}}{2};\dfrac{-1-\sqrt{21}}{2}\right\}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
\(u_3=u_1+2d;u_2=u_1+d;u_7=u_1+6d\\ Có:\left\{{}\begin{matrix}u_3-u_7=-8\\u_2.u_7=75\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left(u_1+2d\right)-\left(u_1+6d\right)=-8\\\left(u_1+d\right).\left(u_1+6d\right)=75\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-4d=-8\\u_1^2+7u_1d+6d^2=75\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}d=2\\u^2_1+14u_1+24=75\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}d=2\\u_1^2+14u_1-51=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}d=2\\u_1^2-3u_1+17u_1-51=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}d=2\\u_1\left(u_1-3\right)+17\left(u_1-3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}d=2\\\left(u_1+17\right)\left(u_1-3\right)=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}d=2\\\left[{}\begin{matrix}u_1+17=0\\u_1-3=0\end{matrix}\right.\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}d=2\\\left[{}\begin{matrix}u_1=-17\\u_1=3\end{matrix}\right.\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 1:
\(a\in\left(-\Omega;-\dfrac{\Omega}{2}\right)\)
=>\(cosa< 0\)
\(sin^2a+cos^2a=1\)
=>\(cos^2a=1-\left(-\dfrac{2}{3}\right)^2=\dfrac{5}{9}\)
mà cosa<0
nên \(cosa=-\dfrac{\sqrt{5}}{3}\)
\(sin2a=2\cdot sina\cdot cosa=2\cdot\dfrac{-2}{3}\cdot\dfrac{-\sqrt{5}}{3}=\dfrac{4\sqrt{5}}{9}\)
Đúng 0
Bình luận (0)
Một người đi làm với mức lương khởi điểm là 6 triệu đồng một tháng. Cứ sau 6 tháng, lượng người đó tăng thêm 5%. Tính tổng số lương người đó nhận được sau mười năm đi làm.
Lời giải:
Sau 10 năm đi làm ~ 120 tháng ~ 20 lần tăng lương.
Lương sau 10 năm là:
$6(1+5\text{%})^20=15,92$ (triệu đồng)
Đúng 0
Bình luận (0)
Cho bốn số a,b,c,d biết rằng a,b,c theo thứ tự đó lập thành một cấp số nhân công bội q>1; còn b,c,d theo thứ tự đó lập thành cấp số cộng. Tìm q biết rằng a+d=14 và b+c=12. Giúp mình với mng ơi <3
Tìm các số thực x,y sao cho ba số x + 1; x + 2y và 3y + 3 theo thứ tự là 1 cấp số cộng, đồng thời 3 số x + 1; y + 1 và 3y - 1 theo thứ tự là 1 cấp số nhân.
Vì `x+1;x+2y;3y+3` là `1` CSC `=>2x+4y=x+1+3y+3<=>x=4-y` `(1)`
Vì `x+1;y+1;3y-1` là `1` CSN `=>(y+1)^2=(x+1)(3y-1)` `(2)`
Từ `(1);(2)=>y^2+2y+1=(4-y+1)(3y-1)`
`<=>y^2+2y+1=-3y^2+y+15y-5`
`<=>[(y=3),(y=1/2):}`
`=>[(x=1),(x=7/2):}`
Đúng 1
Bình luận (0)
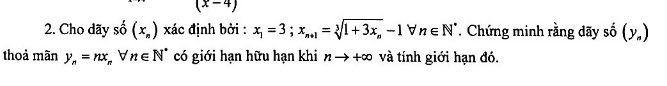
giúp em câu này với ạ em cảm ơn nhiềuuuu
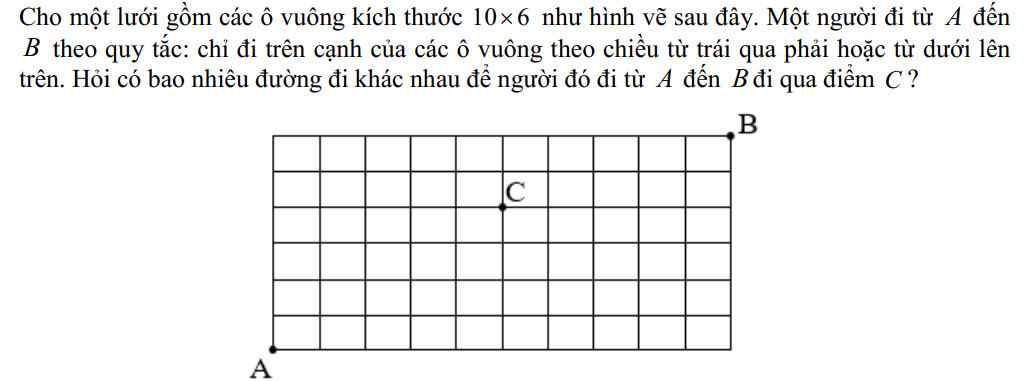
giup em voi em cam on nhieu aaa
Từ A đến C, có 4 đoạn đi lên (nằm song song nhau) và 5 đoạn đi ngang nằm song song
Ta kí hiệu đi lên là L và đi ngang là N, như vậy, số cách đi từ A đến C là số cách sắp xếp 9 kí tự bao gồm 4L và 5N
\(\Rightarrow\) Có \(\dfrac{9!}{5!.4!}\) cách
Tương tự, từ C đến B có 2L và 5N, có \(\dfrac{7!}{2!.5!}\) cách
Tổng cộng: \(\dfrac{9!}{5!.4!}.\dfrac{7!}{2!.5!}\) cách đi từ A đến B
Đúng 1
Bình luận (1)

giúp em với ạ em cảm ơn nhiềuu
\(\dfrac{n}{2n-1}>\dfrac{n}{2n}=\dfrac{1}{2}\)
\(\Rightarrow x_{n+1}>\dfrac{1}{2}.\left(\dfrac{x_n^2+2}{x_n}\right)\ge\dfrac{1}{2}.\dfrac{2\sqrt{2x_n^2}}{x_n}=\sqrt{2}\)
Dãy bị chặn dưới bởi \(\sqrt{2}\)
Ta sẽ chứng minh dãy đã cho là dãy giảm, hay \(x_{n+1}-x_n< 0\) với \(n>1\)
\(\Leftrightarrow\dfrac{n}{2n-1}\left(\dfrac{x_n^2+2}{x_n}\right)-x_n< 0\Leftrightarrow\left(1-n\right)x_n^2+2n< 0\)
\(\Leftrightarrow x_n^2>\dfrac{2n}{n-1}\Leftrightarrow x_n>\sqrt{\dfrac{2n}{n-1}}\)
Do \(x_n=\dfrac{n-1}{2\left(n-1\right)-1}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)=\dfrac{n-1}{2n-3}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)\ge\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}\)
Nên ta chỉ cần chứng minh: \(\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}>\sqrt{\dfrac{2n}{n-1}}\)
\(\Leftrightarrow6n-8>0\) (đúng)
Vậy dãy đã cho là dãy giảm
Dãy giảm và bị chặn dưới nên có giới hạn
Gọi giới hạn của dãy là L, lấy giới hạn 2 vế biểu thức truy hồi:
\(\lim\left(x_{n+1}\right)=\lim\left(\dfrac{n}{2n-1}.\dfrac{x_n^2+2}{x_n}\right)\Rightarrow L=\dfrac{1}{2}\left(\dfrac{L^2+2}{L}\right)\)
\(\Rightarrow L^2=2\Rightarrow L=\sqrt{2}\)
Đúng 1
Bình luận (2)




