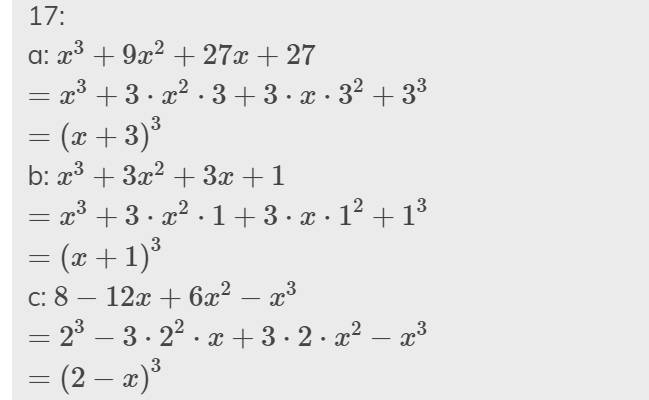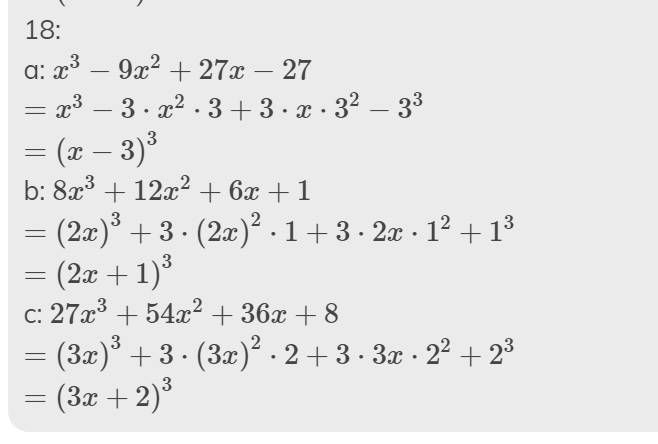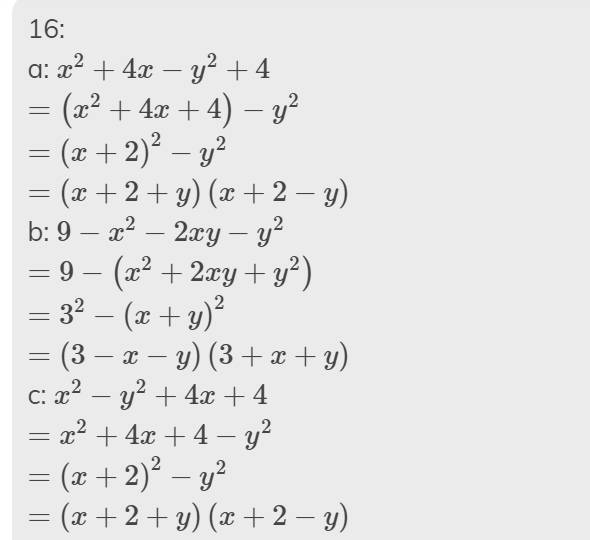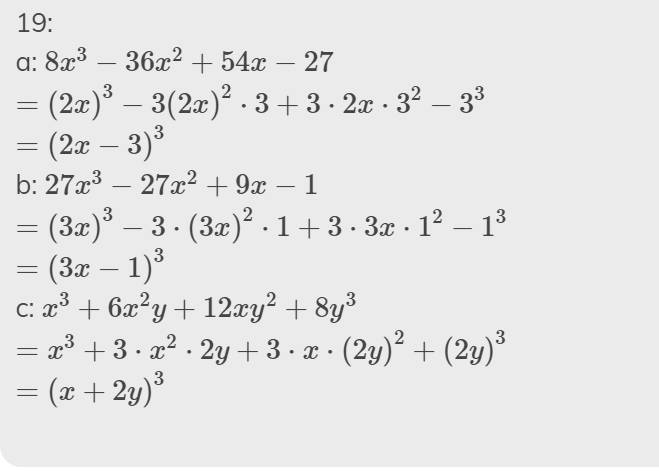Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức

a) \(x^2+5x-6\)

\(=x^2-x+6x-6\)

\(=\left(x^2-x\right)+\left(6x-6\right)\)

\(=x\left(x-1\right)-6\left(x-1\right)\)

\(=\left(x-1\right)\left(x-6\right)\)

b) \(a^2+4a+3\)

\(=a^2+a+3a+3\)

\(=\left(a^2+a\right)+\left(3a+3\right)\)

\(=a\left(a+1\right)+3\left(a+1\right)\)

\(=\left(a+1\right)\left(a+3\right)\)

c) \(16y-5y^2-3\)

\(=-5y^2+y+15y-3\)

\(=\left(-5y^2+y\right)+\left(15y-3\right)\)

\(=-y\left(5y-1\right)+3\left(5y-1\right)\)

\(=\left(5y-1\right)\left(3-y\right)\)

a: \(x^2+5x-6\)

\(=x^2+6x-x-6\)

\(=x\left(x+6\right)-\left(x+6\right)\)

\(=\left(x+6\right)\left(x-1\right)\)

b: \(a^2+4a+3\)

\(=a^2+a+3a+3\)

\(=a\left(a+1\right)+3\left(a+1\right)\)

\(=\left(a+1\right)\left(a+3\right)\)

c: \(16y-5y^2-3\)

\(=-5y^2+15y+y-3\)

\(=-5y\cdot\left(y-3\right)+\left(y-3\right)\)

\(=\left(y-3\right)\left(-5y+1\right)\)

1: Đa thức này ko phân tích được nha bạn

2: \(x^2+8x+7\)

\(=x^2+x+7x+7\)

\(=x\left(x+1\right)+7\left(x+1\right)\)

\(=\left(x+1\right)\left(x+7\right)\)

3: \(x^2-6x-16\)

\(=x^2-8x+2x-16\)

\(=x\left(x-8\right)+2\left(x-8\right)\)

\(=\left(x-8\right)\left(x+2\right)\)

4: \(4x^2-8x+3\)

\(=4x^2-2x-6x+3\)

\(=2x\left(2x-1\right)-3\left(2x-1\right)\)

\(=\left(2x-1\right)\left(2x-3\right)\)

5: \(3x^2-11x+6\)

\(=3x^2-9x-2x+6\)

\(=3x\left(x-3\right)-2\left(x-3\right)\)

\(=\left(x-3\right)\left(3x-2\right)\)

16:

a: \(x^2+4x-y^2+4\)

\(=\left(x^2+4x+4\right)-y^2\)

\(=\left(x+2\right)^2-y^2\)

\(=\left(x+2+y\right)\left(x+2-y\right)\)

b: \(9-x^2-2xy-y^2\)

\(=9-\left(x^2+2xy+y^2\right)\)

\(=3^2-\left(x+y\right)^2\)

\(=\left(3-x-y\right)\left(3+x+y\right)\)

c: \(x^2-y^2+4x+4\)

\(=x^2+4x+4-y^2\)

\(=\left(x+2\right)^2-y^2\)

\(=\left(x+2+y\right)\left(x+2-y\right)\)

19:

a: \(8x^3-36x^2+54x-27\)

\(=\left(2x\right)^3-3\left(2x\right)^2\cdot3+3\cdot2x\cdot3^2-3^3\)

\(=\left(2x-3\right)^3\)

b: \(27x^3-27x^2+9x-1\)

\(=\left(3x\right)^3-3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2-1^3\)

\(=\left(3x-1\right)^3\)

c: \(x^3+6x^2y+12xy^2+8y^3\)

\(=x^3+3\cdot x^2\cdot2y+3\cdot x\cdot\left(2y\right)^2+\left(2y\right)^3\)

\(=\left(x+2y\right)^3\)

17:

a: \(x^3+9x^2+27x+27\)

\(=x^3+3\cdot x^2\cdot3+3\cdot x\cdot3^2+3^3\)

\(=\left(x+3\right)^3\)

b: \(x^3+3x^2+3x+1\)

\(=x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3\)

\(=\left(x+1\right)^3\)

c: \(8-12x+6x^2-x^3\)

\(=2^3-3\cdot2^2\cdot x+3\cdot2\cdot x^2-x^3\)

\(=\left(2-x\right)^3\)

18:

a: \(x^3-9x^2+27x-27\)

\(=x^3-3\cdot x^2\cdot3+3\cdot x\cdot3^2-3^3\)

\(=\left(x-3\right)^3\)

b: \(8x^3+12x^2+6x+1\)

\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot1+3\cdot2x\cdot1^2+1^3\)

\(=\left(2x+1\right)^3\)

c: \(27x^3+54x^2+36x+8\)

\(=\left(3x\right)^3+3\cdot\left(3x\right)^2\cdot2+3\cdot3x\cdot2^2+2^3\)

\(=\left(3x+2\right)^3\)

Bài 9.

\(a,x^2-9\\=x^2-3^2\\=(x-3)(x+3)\\b,49-x^2\\=7^2-x^2\\=(7-x)(7+x)\\c,y^2-81\\=y^2-9^2\\=(y-9)(y+9)\)

Bài 10.

\(a,y^2-121\\=y^2-11^2\\=(y-11)(y+11)\\b,y^2-169\\=y^2-13^2\\=(y-13)(y+13)\\c,y^2-256\\=y^2-16^2\\=(y-16)(y+16)\)

Bài 8.

\(a,-x^2-4y^2+4xy\)

\(=-\left(x^2+4y^2-4xy\right)\)

\(=-\left(x^2-4xy+4y^2\right)\)

\(=-\left[x^2-2\cdot x\cdot2y+\left(2y\right)^2\right]\)

\(=-\left(x-2y\right)^2\)

\(b,-x^4+2x^2-1\)

\(=-\left(x^4-2x^2+1\right)\)

\(=-\left[\left(x^2\right)^2-2\cdot x^2\cdot1+1^2\right]\)

\(=-\left(x^2-1\right)^2\)

\(=-\left(x-1\right)^2\left(x+1\right)^2\)

\(c,x^4+4-4x^2\)

\(=x^4-4x^2+4\)

\(=\left(x^2\right)^2-2\cdot x^2\cdot2+2^2\)

\(=\left(x^2-2\right)^2\)

6:

a: \(4x^2+20xy+25y^2\)

\(=\left(2x\right)^2+2\cdot2x\cdot5y+\left(5y\right)^2\)

\(=\left(2x+5y\right)^2\)

b: \(25x^2+10xy+y^2\)

\(=\left(5x\right)^2+2\cdot5x\cdot y+y^2\)

\(=\left(5x+y\right)^2\)

7:

a: \(10x-x^2-25\)

\(=-\left(x^2-10x+25\right)\)

\(=-\left(x^2-2\cdot x\cdot5+5^2\right)\)

\(=-\left(x-5\right)^2\)

b: \(-x^2-2xy-y^2\)

\(=-\left(x^2+2\cdot x\cdot y+y^2\right)\)

\(=-\left(x+y\right)^2\)

c: \(-x^2+20x-100\)

\(=-\left(x^2-20x+100\right)\)

\(=-\left(x^2-2\cdot x\cdot10+10^2\right)\)

\(=-\left(x-10\right)^2\)

Bài 1

a) x² - 4x + 4

= (x - 2)²

b) x² - 6x + 9

= (x - 3)²

c) x² - 10x + 25

= (x - 5)²

Bài 2

a) 4x² - 12x + 9

= (2x - 3)²

b) 25x² - 20x + 4

= (5x - 2)²

c) 1/9 x² - 10/3 x + 25

= (x/3 - 5)²

Bài 3

a) 4x² - 12xy + 9y²

= (2x - 3y)²

b) 9x² - 30xy + 25y²

= (3x - 5y)²

c) 1/4 y² - 1/3 xy + 1/9 x²

= (y/2 - x/3)²

Bài 4

a) y² + 8y + 16

= (y + 4)²

b) y² + 12y + 36

= (y + 6)²

c) y² - 4y + 4

= (y - 2)²

\(4x^2+4x-3\)

\(=4x^2+6x-2x-3\)

\(=\left(4x^2+6x\right)-\left(2x+3\right)\)

\(=2x\left(2x+3\right)-\left(2x+3\right)\)

\(=\left(2x+3\right)\left(2x-1\right)\)

\(a)\)  \( 49(y-4)^2-9(y+2)^2\)

\(=[7(y-4)]^2-[3(y+2)]^2\)

\(=[7(y-4)-3(y+2)][7(y-4)+3(y+2)]\)

\(=(7y-28-3y-6)(7y-28+3y+6)\)

\(=(4y-34)(10y-22)\)

\(b)\)   \((a^2+b^2-5)^2-2(ab+2)^2\)

\(=\left(a^2+b^2-5\right)^2-\left[\sqrt{2}\left(ab+2\right)\right]^2\)

Xem lại đề...

\(\dfrac{x^2}{2}-2x^2\)

\(=\dfrac{1}{2}x^2-2x^2\)

\(=-\dfrac{3}{2}x^2\) 

1) \(x\left(x-1\right)+\left(1-x\right)^2\)

\(=x\left(x-1\right)+\left(x-1\right)^2\)

\(=\left(x-1\right)\left(x+x-1\right)\)

\(=\left(x-1\right)\left(2x-1\right)\)

2) \(2x\left(x-2\right)-\left(x-2\right)^2\)

\(=\left(x-2\right)\left[2x-\left(x-2\right)\right]\)

\(=\left(x-2\right)\left(2x-x+2\right)\)

\(=\left(x-2\right)\left(x+2\right)\) 

3) \(3x\left(x-1\right)^2-\left(1-x\right)^3\)

\(=3x\left(x-1\right)^2+\left(x-1\right)^3\)

\(=\left(x-1\right)^2\left(3x+x-1\right)\)

\(=\left(x-1\right)^2\left(4x-1\right)\)

4) \(3x\left(x+2\right)-5\left(x+2\right)^2\)

\(=\left(x+2\right)\left[3x-5\left(x+2\right)\right]\)

\(=\left(x+2\right)\left(3x-5x-10\right)\)

\(=\left(x+2\right)\left(-2x-10\right)\)

\(=-2\left(x+2\right)\left(x+5\right)\)