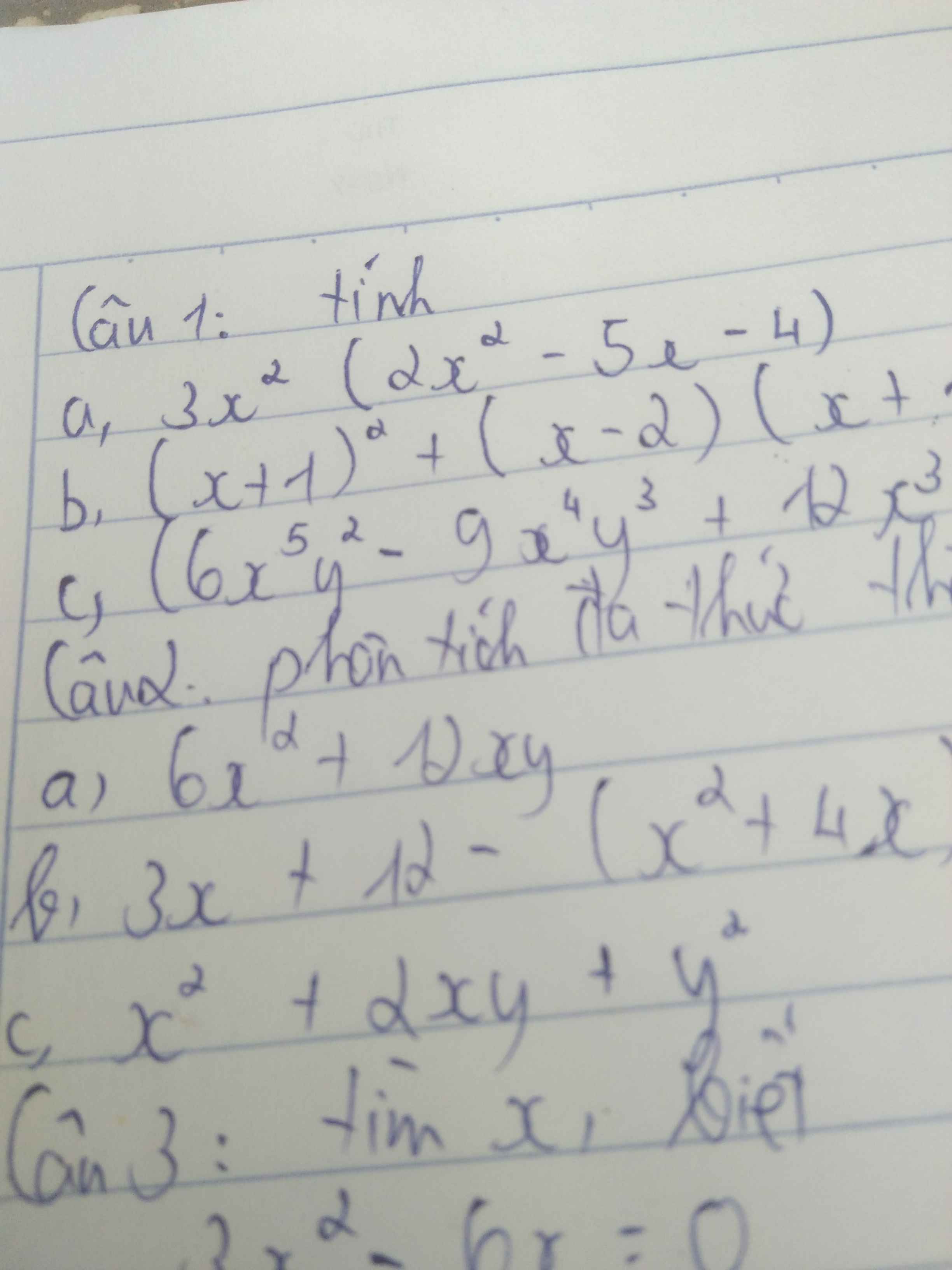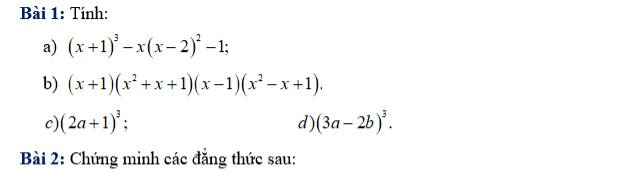\(a,\left(x+1\right)^3-x\left(x-2\right)^2-1\\ =\left(x^3+3x^2+3x+1\right)-x\left(x^2-4x+4\right)-1\\ =x^3-x^3+3x^2+4x^2+3x-4x+1-1\\ =7x^2-x\\ ---\\ b,\left(x+1\right)\left(x^2+x+1\right)\left(x-1\right)\left(x^2-x+1\right)\\ =\left[\left(x+1\right)\left(x^2-x+1\right)\right].\left[\left(x-1\right)\left(x^2+x+1\right)\right]=\left(x^3+1\right)\left(x^3-1\right)=x^6-1\\ ---\\ c,\left(2x+1\right)^3=\left(2a\right)^3+3.\left(2a\right)^2.1+3.2a.1^2+1^3=8a^3+12a^2+6a+1\\ d,\left(3a-2b\right)^3=\left(3a\right)^3-3.\left(3a\right)^2.2b+3.3a.\left(2b\right)^2-\left(2b\right)^3\\ =27a^3-54a^2b+36ab^2-8b^3\)
Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Chi tiết nhất ạ e cảm ơn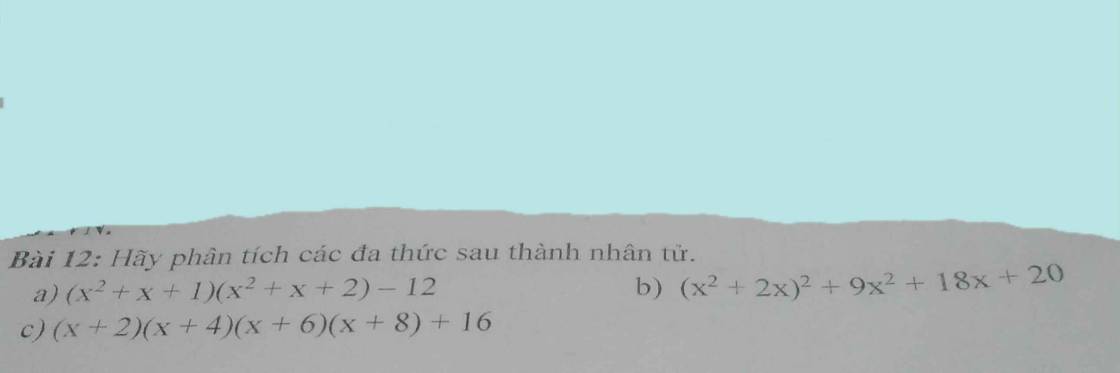
Phân tích đa thức thành phân tử : ax - 2x -a² + 2a Giải chi tiết giúp e vs ạ
Thực hiện phép chia:( chi tiết cho mình nhed, mình cảm ơn ạ)
Ta có:
A(x)= 6x3 - 7x2 - x + m; B(x)= 2x + 1
Hãy thực hiện phép chia A(x) cho B(x).
lm chi tiết
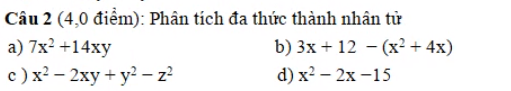
Chi tiết nhâtz
Chi tiết  nhất
nhất
1) Tìm số nguyên a sao cho đa thức (x+a)(x-5)+2 phân tích được thành (x+b)(x+c) với b,c là các số nguyên
2) Phân tích đa thức thành nhân tử: x^7+x^2-1
3) Phân tích đa thức thành nhân tử: x^4-6x^3+12x^2-14x+3
M.n giúp mink vs cần gấp và chi tiết nha
Thank you trước
Đọc tiếp
1) Tìm số nguyên a sao cho đa thức (x+a)(x-5)+2 phân tích được thành (x+b)(x+c) với b,c là các số nguyên
2) Phân tích đa thức thành nhân tử: x\(^7\)+x\(^2\)-1
3) Phân tích đa thức thành nhân tử: x\(^4\)-6x\(^3\)+12x\(^2\)-14x+3
M.n giúp mink vs cần gấp và chi tiết nha
Thank you trước
phân tích đa thức sau thành nhân tử(x3-2xy+3x2).(x-2y)tành nhân tử
giúp em với ạ!em cảm ơn ạ!
giúp với ạ