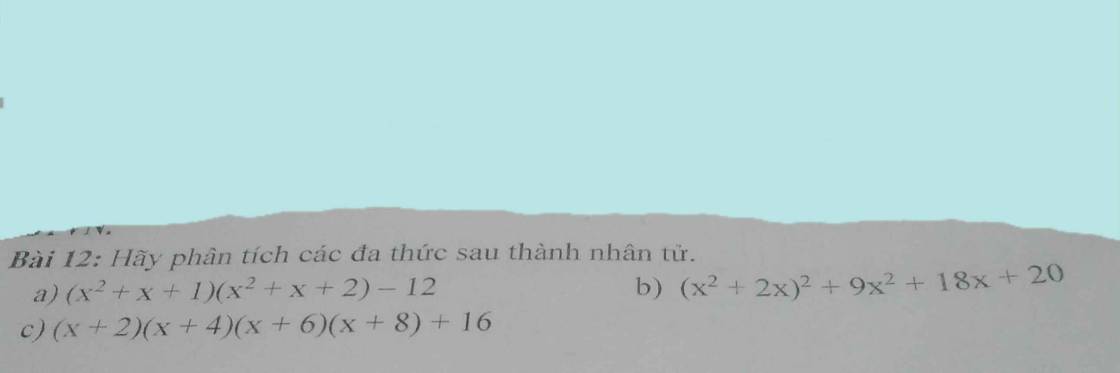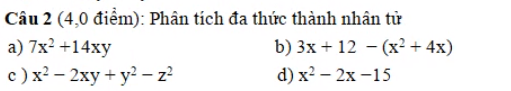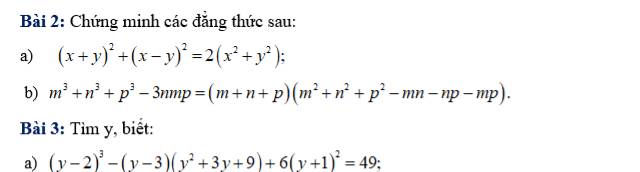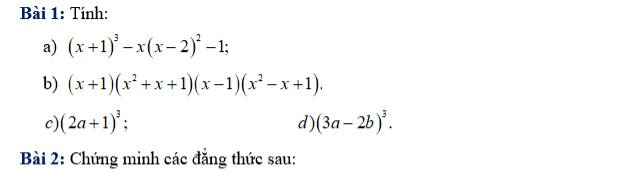a: \(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
\(=\left(x^2+x\right)^2+2\left(x^2+x\right)+\left(x^2+x\right)+2-12\)
\(=\left(x^2+x\right)^2+3\left(x^2+x\right)-10\)
\(=\left(x^2+x\right)^2+5\left(x^2+x\right)-2\left(x^2+x\right)-10\)
\(=\left(x^2+x\right)\left(x^2+x+5\right)-2\left(x^2+x+5\right)\)
\(=\left(x^2+x+5\right)\left(x^2+x-2\right)\)
\(=\left(x^2+x+5\right)\left(x^2+2x-x-2\right)\)
\(=\left(x^2+x+5\right)\left[x\left(x+2\right)-\left(x+2\right)\right]\)
\(=\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
b: \(\left(x^2+2x\right)^2+9x^2+18x+20\)
\(=\left(x^2+2x\right)^2+9\left(x^2+2x\right)+20\)
\(=\left(x^2+2x\right)^2+4\left(x^2+2x\right)+5\left(x^2+2x\right)+20\)
\(=\left(x^2+2x\right)\left(x^2+2x+4\right)+5\left(x^2+2x+4\right)\)
\(=\left(x^2+2x+4\right)\left(x^2+2x+5\right)\)
c: \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)
\(=\left(x+2\right)\left(x+8\right)\left(x+4\right)\left(x+6\right)+16\)
\(=\left(x^2+8x+2x+16\right)\left(x^2+6x+4x+24\right)+16\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)
\(=\left(x^2+10x\right)^2+24\left(x^2+10x\right)+16\left(x^2+10x\right)+384+16\)
\(=\left(x^2+10x\right)^2+40\left(x^2+10x\right)+400\)
\(=\left(x^2+10x+20\right)^2\)