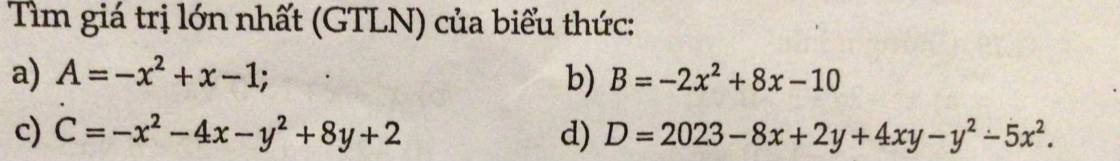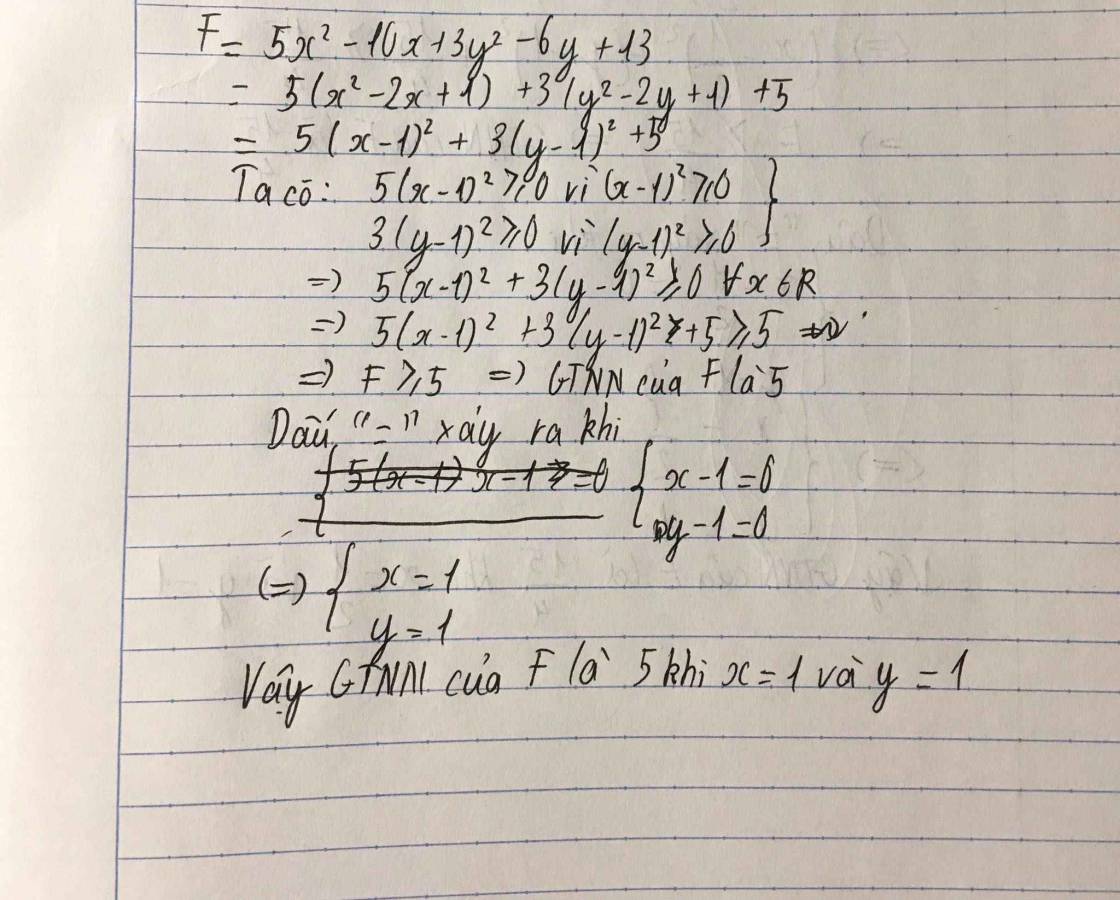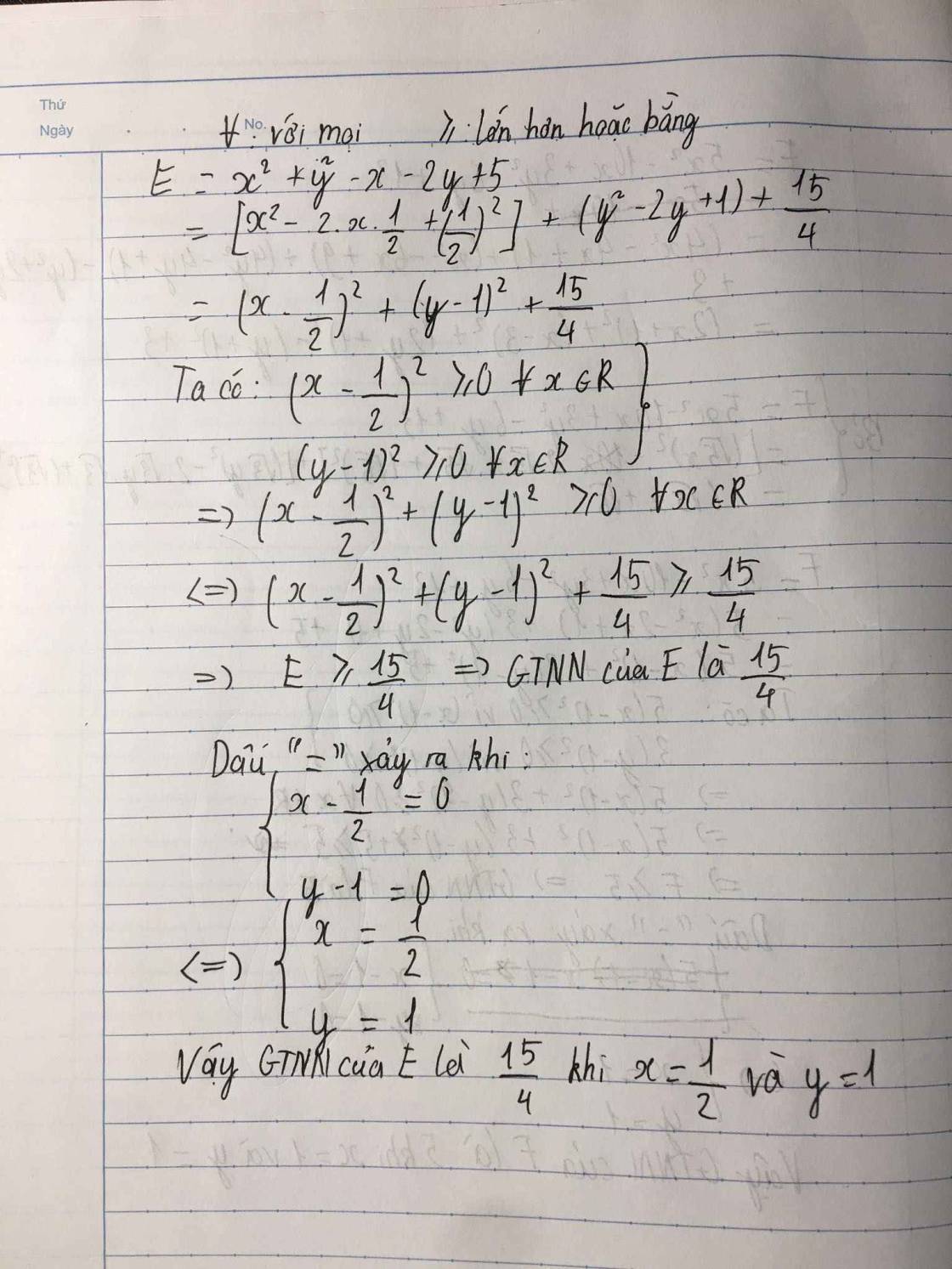Bài 3: Những hằng đẳng thức đáng nhớ

Lời giải:

a. Đề có vẻ sai.

b. $(5-x)^2-(x+3)(x-7)=15$

$\Leftrightarrow (x^2-10x+25)-(x^2-4x-21)=15$
$\Leftrightarrow -6x+31=0$

$\Leftrightarrow x=\frac{31}{6}$

c.

$(3x-1)^2+11=9x(x-1)$
$\Leftrightarrow 9x^2-6x+1+11=9x^2-9x$

$\Leftrightarrow 3x+12=0$

$\Leftrightarrow x=-4$

d.

$(2x-3)^2-7x=4x^2-5x+2$
$\Leftrightarrow 4x^2-12x+9-7x=4x^2-5x+2$
$\Leftrightarrow -19x+9=-5x+2$
$\Leftrightarrow 7=14x$

$\Leftrightarrow x=\frac{1}{2}$

a)

\(A=-x^2+x-1\\ =-\left(x^2-x+1\right)\\ =-\left(x^2-2.\dfrac{1}{2}.x+\dfrac{1}{4}\right)+\dfrac{5}{4}\\ =-\left(x-\dfrac{1}{2}\right)^2+\dfrac{5}{4}\le\dfrac{5}{4}\)

GTLN của A đạt \(\dfrac{5}{4}\) khi và chỉ khi \(x-\dfrac{1}{2}\)

b)

\(B=-2x^2+8x-10\\ =-2\left(x^2-4x+5\right)\\ =-2\left(x^2-4x+4+1\right)\\ =-2\left(x^2-4x+4\right)-2\\ =-2\left(x-2\right)^2-2\le-2\)

GTLN của B đạt \(-2\) khi và chỉ khi \(x=2\)

`#3107`

`a)`

`(6x - 2)^2 + 4(3x - 1)(2 + y) + (y + 2)^2 - (6x + y)^2`

`= [(6x - 2)^2 - (6x + y)^2] + 4(3x - 1)(2 + y) + (2 + y)^2`

`= (6x - 2 - 6x - y)(6x -2 + 6x + y) + (2 + y)*[ 4(3x - 1) + 2 + y]`

`= (2 - y)(12x + y - 2) + (2 + y)*(12x - 4 + 2 + y)`

`= (2 - y)(12x + y - 2) + (2 + y)*(12x + y - 2)`

`= (12x + y - 2)(2 - y + 2 + y)`

`= (12x + y - 2)*4`

`= 48x + 4y - 8`

`b)`

\(5(2x-1)^2+2(x-1)(x+3)-2(5-2x)^2-2x(7x+12)\)

`= 5(4x^2 - 4x + 1) + 2(x^2 + 2x - 3) - 2(25 - 20x + 4x^2) - 14x^2 - 24x`

`= 20x^2 - 20x + 5 + 2x^2 + 4x - 6 - 50 + 40x - 8x^2 - 14x^2 - 24x`

`= - 51`

`c)`

\(2(5x-1)(x^2-5x+1)+(x^2-5x+1)^2+(5x-1)^2-(x^2-1)(x^2+1)\)

`= [ 2(5x - 1) + x^2 - 5x + 1] * (x^2 - 5x + 1) + (5x - 1)^2 - [ (x^2)^2 - 1]`

`= (10x - 2 + x^2 - 5x + 1) * (x^2 - 5x + 1) + (5x - 1)^2 - x^4 + 1`

`= (x^2 + 5x - 1)(x^2 - 5x + 1) + (5x - 1)^2 - x^4 + 1`

`= x^4 - (5x - 1)^2 + (5x - 1)^2 - x^4 + 1`

`= 1`

`d)`

\((x^2+4)^2-(x^2+4)(x^2-4)(x^2+16)-8(x-4)(x+4)\)

`= (x^2 + 4)*[x^2 + 4 - (x^2 - 4)(x^2 + 16)] - 8(x^2 - 16)`

`= (x^2 + 4)(x^4 + 12x^2 - 64) - 8x^2 + 128`

`= x^6 + 16x^4 - 16x^2 - 256 - 8x^2 + 128`

`= x^6 + 16x^4 - 24x^2 - 128`

\(x^2-5x+7\)

\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2-\dfrac{25}{4}+7\)

\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\)

Ta thấy: \(\left(x-\dfrac{5}{2}\right)^2\ge0\forall x\)

\(\Rightarrow\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\forall x\)

hay \(x^2-5x+7>0\forall x\).

Vậy ...

#\(Toru\)

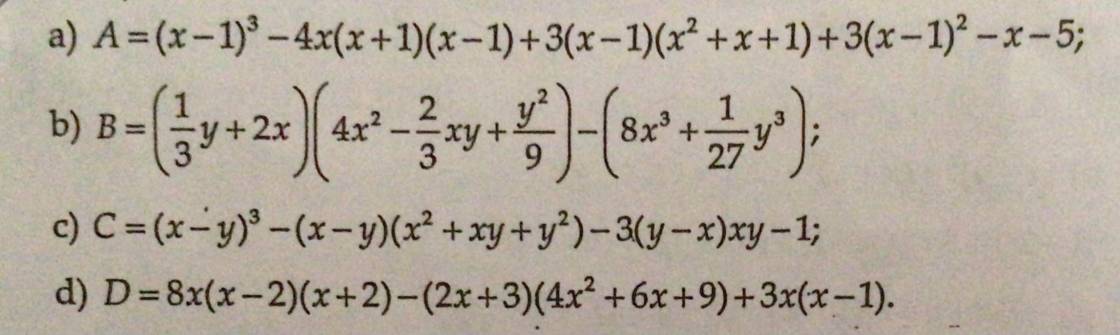
\(D=8x\left(x-2\right)\left(x+2\right)-\left(2x+3\right)\left(4x^2+6x+9\right)+3x\left(x-1\right)\\ =8x\left(x^2-4\right)-\left(2x+3\right)\left(2x+3\right)^2+3x\left(x-1\right)\\ =8x^3-32x-\left(2x+3\right)^3+3x^2-3x\\ =8x^3-32x-\left(8x^3+36x^2+54x+27\right)+3x^2-3x\\ =\left(8x^3-8x^3\right)-\left(36x^2-3x^2\right)-\left(32x+54x+3x\right)-27\\ =-33x^2+89x-27\)

\(B=\left(\dfrac{1}{3}y+2x\right)\left(4x^2-\dfrac{2}{3}xy+\dfrac{y^2}{9}\right)-\left(8x^3+\dfrac{1}{27}y^3\right)\\ =\left(\dfrac{1}{3}y+2x\right)\left[\left(2x\right)^2-2x.\dfrac{1}{3}y+\left(\dfrac{1}{3}y\right)^2\right]-\left[\left(2x\right)^3+\left(\dfrac{1}{3}y\right)^3\right]\\ =\left[\left(2x\right)^3+\left(\dfrac{1}{3}y\right)^3\right]-\left[\left(2x\right)^3+\left(\dfrac{1}{3}y\right)^3\right]\\ =0\)

\(A=\left(x-1\right)^3-4x\left(x+1\right)\left(x-1\right)+3\left(x-1\right)\left(x^2+x+1\right)+3\left(x-1\right)^2-x-5\\ =\left(x^3-3x^2+3x-1\right)-4x\left(x^2-1\right)+3\left(x^3-1\right)+3\left(x^2-2x+1\right)-x-5\\ =x^3-3x^2+3x-1-4x^3+4x+3x^3-3+3x^2-6x+3-x-5\\ =\left(x^3-4x^3+3x^3\right)+\left(3x^2-3x^2\right)+\left(3x+4x-6x-x\right)-\left(1+3-3+5\right)\\ =0+0+0-6=-6\)

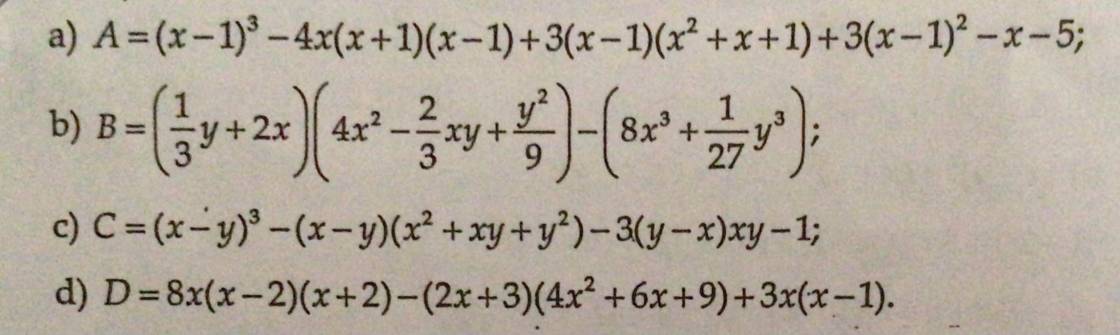
a: \(A=\left(x-1\right)^3-4x\left(x+1\right)\left(x-1\right)+3\left(x-1\right)\left(x^2+x+1\right)+3\left(x-1\right)^2-x-5\)

\(=x^3-3x^2+3x-1+3\left(x^3-1\right)-4x\left(x^2-1\right)+3\left(x^2-2x+1\right)-x-5\)

\(=4x^3-3x^2+3x-4-4x^3+4x+3x^2-6x+3-x-5\)

\(=-6\)

b: \(B=\left(2x+\dfrac{1}{3}y\right)\left(4x^2-\dfrac{2}{3}xy+\dfrac{1}{9}y^2\right)-\left(8x^3+\dfrac{1}{27}y^3\right)\)

\(=\left(2x+\dfrac{1}{3}y\right)\left[\left(2x\right)^2-2x\cdot\dfrac{1}{3}y+\left(\dfrac{1}{3}y\right)^2\right]-8x^3-\dfrac{1}{27}y^3\)

\(=8x^3+\dfrac{1}{27}y^3-8x^3-\dfrac{1}{27}y^2=0\)

c: \(C=\left(x-y\right)^3-\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\left(y-x\right)-1\)

\(=x^3-3x^2y+3xy^2-y^3-x^3+y^3-3xy^2+3x^2y-1\)

=-1

d: \(D=8x\left(x-2\right)\left(x+2\right)-\left(2x+3\right)\left(4x^2+6x+9\right)+3x\left(x-1\right)\)

\(=8x\left(x^2-4\right)-8x^3-27+3x^2-3x\)

\(=8x^3-32x-8x^3+3x^2-3x-27\)

\(=3x^2-35x-27\)

\(B=\left(x+y\right)^3+3\left(x-y\right)\left(x+y\right)^2+3\left(x-y\right)^2\left(x+y\right)+\left(x-y\right)^3\)

\(=\left(x+y\right)^3+3\cdot\left(x+y\right)^2\cdot\left(x-y\right)+3\cdot\left(x+y\right)\cdot\left(x-y\right)^2+\left(x-y\right)^3\)

\(=\left[\left(x+y\right)+\left(x-y\right)\right]^3\)

\(=\left(x+y+x-y\right)^3\)

\(=\left(2x\right)^3\)

\(=8x^3\)

\(---\)

\(C=8\left(x+2y\right)^3-6\left(x+2y\right)^2x+12\left(x+2y\right)x^2-8x^3\) (sửa đề)

\(=\left[2\left(x+2y\right)\right]^3-3\cdot\left(x+2y\right)^2\cdot2x+3\cdot\left(x+2y\right)\cdot\left(2x\right)^2-\left(2x\right)^3\)

\(=\left[2\left(x+2y\right)-2x\right]^3\)

\(=\left(2x+4y-2x\right)^3\)

\(=\left(4y\right)^3\)

\(=64y^3\)

\(---\)

\(D=\left(x-y\right)^3-3\cdot\dfrac{\left(x-y\right)^2}{2}\cdot y+3\cdot\dfrac{\left(x-y\right)}{4}\cdot y^2-\dfrac{y^3}{8}\)

\(=\left(x-y\right)^3-3\cdot\left(x-y\right)^2\cdot\dfrac{y}{2}+3\cdot\left(x-y\right)\cdot\left(\dfrac{y}{2}\right)^2-\left(\dfrac{y}{2}\right)^3\)

\(=\left[\left(x-y\right)-\dfrac{y}{2}\right]^3\)

\(=\left(x-y-\dfrac{y}{2}\right)^3\)

\(=\left(x-\dfrac{3}{2}y\right)^3\)

#\(Toru\)

\(1) ( 2x+1)^2 + 2(2x+1) + 1\)

\(=\left(2x+1\right)^2+2\cdot\left(2x+1\right)\cdot1+1^2\)

\(=\left(2x+1+1\right)^2\)

\(=\left(2x+2\right)^2\)

\(2) (3x-2y)^2+4(3x-2y)+4\)

\(=\left(3x-2y\right)^2+2\cdot\left(3x-2y\right)\cdot2+2^2\)

\(=\left(3x-2y+2\right)^2\)

#\(Toru\)

`# \text {04th5.}`

`1)`

`(2x + 1)^2 + 2(2x + 1) + 1`

`= 4x^2 + 4x + 1 + 4x + 2 + 1`

`= 4x^2 + 8 + 4`

`2)`

`(3x - 2y)^2 + 4(3x - 2y) + 4`

`= 9x^2 - 12xy + 4y^2 + 12x - 8y + 4`

\(27x^3+27x^2+9x+1\)

\(=\left(3x\right)^3+3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2+1^3\)

\(=\left(3x+1\right)^3\)

=(3x)^3+3*(3x)^2*1+3*3x*1^2+1^3

=(3x+1)^3

Để tính giá trị của biểu thức 27x^3 + 27x^2 + 9x + 1, chúng ta thực hiện các phép tính theo thứ tự từ trái qua phải:

27x^3 + 27x^2 + 9x + 1 = (27x^3 + 27x^2) + (9x + 1) = 27x^2(x + 1) + 9x + 1

Vậy giá trị của biểu thức là 27x^2(x + 1) + 9x + 1.