Hơn một năm rùi mới vào lại đây kỉ niệm ghê:))
Hơn một năm rùi mới vào lại đây kỉ niệm ghê:))
E=-x(x-y)^2+(x-y)^3+y^2(y-2x) tại |2x-1|=1;y=2
|2x-1|=1
=>\(\left[{}\begin{matrix}2x-1=1\\2x-1=-1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x=2\\2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)
\(E=-x\left(x-y\right)^2+\left(x-y\right)^3+y^2\left(y-2x\right)\)
\(=\left(x-y\right)^2\left[-x+x-y\right]+y^2\left(y-2x\right)\)
\(=\left(x-y\right)^2\cdot\left(-y\right)+y^2\left(y-2x\right)\)
\(=-y\left(x^2-2xy+y^2\right)+y^3-2xy^2\)
\(=-x^2y+2xy^2-y^3+y^3-2xy^2\)
\(=-x^2y\)
Thay x=1 và y=2 vào E, ta được: \(E=-1^2\cdot2=-2\)
Thay x=0 và y=2 vào E, ta được: \(E=-0^2\cdot2=0\cdot2=0\)
\(VT=(x+y)(x^3-x^2y+xy^2+y^3)\\=x(x^3-x^2y+xy^2+y^3)+y(x^3-x^2y+xy^2+y^3)\\=x^4-x^3y+x^2y^2+xy^3+x^3y-x^2y^2+xy^3+y^4\\=x^4+y^4+(-x^3y+x^3y)+(x^2y^2-x^2y^2)+(xy^3+xy^3)\\=x^4+y^4+2xy^3\)
Cậu xem lại đề giúp mình nhé!
\(VT=\left(x+y\right)\left(x^3-x^2y+xy^2+y^3\right)\)
`= x^4 -x^3y+x^2y^2+xy^3 +x^3y-x^2y^2 +xy^3 +y^4`
`= (-x^3y +x^3y) +(x^2y^2-x^2y^2) +(xy^3 +xy^3) +x^4+y^4`
`= 2xy^3+x^4+y^4`
Đề có sai ko c...
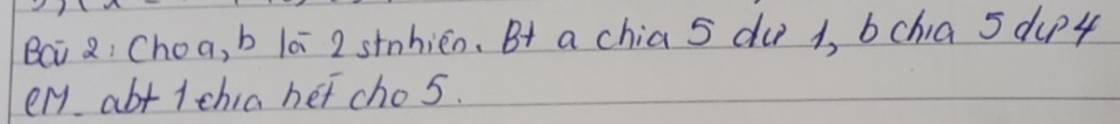 help tui:(
help tui:(
Giả sử hai số a;b theo đề bài có dạng là : \(\left\{{}\begin{matrix}a=5k+1\left(k\in N\right)\\b=5k+4\left(k\in N\right)\end{matrix}\right.\)
Ta có thể giải quyết bài toán này như sau :
Xét tổng : \(ab+1=\left(5k+1\right)\left(5k+4\right)+1\)
\(=25k^2+20k+5k+4+1\)
\(=25k^2+25k+5\)
\(=5.\left(5k^2+5k+1\right)⋮5\)
\(\Rightarrow\left(ab+1\right)⋮5\left(đpcm\right)\)
x mũ3 - 3x bình y + x+3xy bình -y-y mũ3
`x^3 - 3x^2y + x + 3xy^2 - y - y^3`
`=(x)^3 - 3*(x)^2*y + 3*x*y^2 - (y)^3 + (x - y)`
`= (x - y)^3 + (x - y)`
`= (x - y)[(x - y)^2 + 1]`
`= (x - y)(x - y - 1)(x - y + 1)`
____
`@` CT:
`(A - B)^3=A^3-3A^2B+3AB^2- B^3`
a. ( 5 - 2x ) ( 5x + 2x ) + 2x ( x + 3 ) = 4 - 2x² b. ( 3x - 2 )( -2x) + 5x² = -x( x - 3) c. 7 - ( 3 + 2x ) (2x - 3 ) = ( x + 4 )²
a: Sửa đề: (5-2x)(5+2x)+2x(x+3)=4-2x^2
=>25-4x^2+2x^2+6x=4-2x^2
=>6x+25=4
=>6x=-21
=>x=-7/2
b: (3x-2)(-2x)+5x^2=-x(x-3)
=>-6x^2+4x+5x^2=-x^2+3x
=>4x=3x
=>x=0
c: =>7-(4x^2-9)=x^2+8x+16
=>7-4x^2+9-x^2-8x-16=0
=>-5x^2-8x=0
=>5x^2+8x=0
=>x(5x+8)=0
=>x=0 hoặc x=-8/5
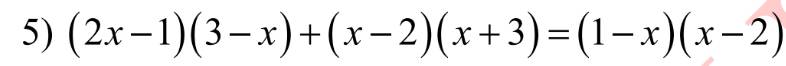
Tìm x biết :
=>6x-2x^2-3+x+x^2+x-6=-(x^2-3x+2)
=>-x^2+8x-9+x^2-3x+2=0
=>5x-7=0
=>x=7/5
\(\left(x+\dfrac{1}{4}\right)\left(x+\dfrac{-1}{4}\right)\left(16x-1\right)\)
\(=\left(x+\dfrac{1}{4}\right)\left(x-\dfrac{1}{4}\right)\left(16x-1\right)\)
\(=\left[x^2-\left(\dfrac{1}{4}\right)^2\right]\cdot\left(16x-1\right)\)
\(=\left(x^2-\dfrac{1}{16}\right)\left(16x-1\right)\)
\(=x^2\left(16x-1\right)-\dfrac{1}{16}\left(16x-1\right)\)
\(=16x^3-x^2-x+\dfrac{1}{16}\)
Bài 1:Rút gọn:
a,(x+2)(x2+4x+4)-(x-2)(x2-4x-4)-12x2-x
b,(x-2)(x+2)(x+3)-(x+1)(x2-x+1)
Ai làm đúng và nhanh giúp, mình tick liền cho ạ
a) Để rút gọn biểu thức (x+2)(x^2+4x+4)-(x-2)(x^2-4x-4)-12x^2-x, ta thực hiện các bước sau:
(x+2)(x^2+4x+4) = x(x^2+4x+4) + 2(x^2+4x+4)
= x^3 + 4x^2 + 4x + 2x^2 + 8x + 8
= x^3 + 6x^2 + 12x + 8
(x-2)(x^2-4x-4) = x(x^2-4x-4) - 2(x^2-4x-4)
= x^3 - 4x^2 - 4x - 2x^2 + 8x + 8
= x^3 - 6x^2 + 4x + 8
Thay vào biểu thức ban đầu, ta có:
(x+2)(x^2+4x+4)-(x-2)(x^2-4x-4)-12x^2-x
= (x^3 + 6x^2 + 12x + 8 - (x^3 - 6x^2 + 4x - 12x^2 - x
= x^3 + 6x^2 + 12x + 8 - x^3 + 6x^2 - 4x - 8 - 12x^2 - x
= 8x + 8 - 4x - 8
= 4x
Vậy biểu thức đã được rút gọn thành 4x.
b) Để rút gọn biểu thức (x-2)(x+2)(x+3)-(x+1)(x^2-x+1), ta thực hiện các bước sau:
(x-2)(x+2) = x^2 - 2^2 = x^2 - 4
Thay vào biểu thức ban đầu, ta có:
(x-2)(x+2)(x+3)-(x+1)(x^2-x+1)
= (x^2 - 4)(x+3) - (x+1)(x^2-x+1)
= x^3 + 3x^2 - 4x - 12 - (x^3 + x^2 - x + x^2 - x + 1)
= x^3 + 3x^2 - 4x - 12 - x^3 - x^2 + x - x^2 + x - 1
= x^3 - x^3 + 3x^2 - x^2 - x^2 + 3x - 4x + x - 12 - 1
= 2x^2 - x - 13
Vậy biểu thức đã được rút gọn thành 2x^2 - x - 13.