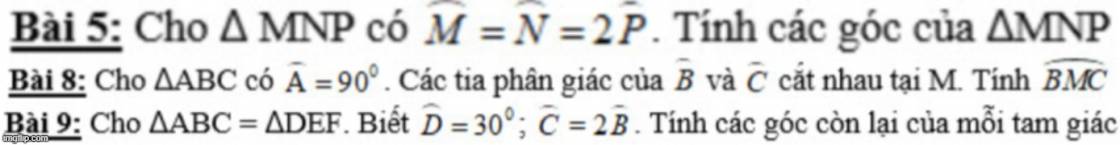
Bài 2: Hai tam giác bằng nhau
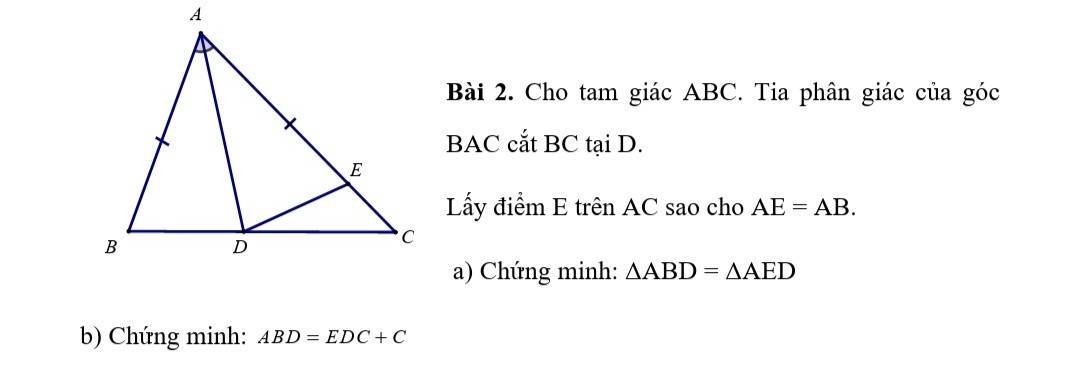
xét tam giác ABD và tam giác AED có
AB=AE(gt)
góc BAD = góc EAD (AD là tia phân giác)
AD chung
Suy ra tam giác ABD = tam giác AED (c-g-c)
Đúng 0
Bình luận (1)
Cho Tam giác abc có ab=ac gọi d là trung điểm cạnh bc.Kẻ de vuông cóc với ab;df vuông góc với ac.Chứng minh
a)Chứng minh tam giác abd=tam giác acd
b)chứng minh ad là tia phân giác của góc bac
c)chứng minh tam giác aed=tam giác afd
d)chứng minh tam giác deb=tam giác dfc
a: Xét ΔABD và ΔACD co
AB=AC
BD=CD
AD chung
=>ΔABD=ΔACD
b: ΔABD=ΔACD
=>góc BAD=góc CAD
=>AD là phân giác của góc BAC
c: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
d: Xét ΔDEB vuông tại E và ΔDFC vuông tại F có
DB=DC
DE=DF
=>ΔDEB=ΔDFC
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A. Gọi M là trung điểm BC. Trên tia đối của tia MA lấy E sao cho MA = ME
a)cm tam giác MAB = tam giác MEC
b) Vì sao AB song song EC
c) cm tam giác BEC vuông tại E
cm là chứng minh
a: Xét ΔMAB và ΔMEC có
MA=ME
góc AMB=góc EMC
MB=MC
Do đó: ΔMAB=ΔMEC
b: Ta có: ΔMAB=ΔMEC
nên góc MAB=góc MEC
=>AB//EC
c: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
góc BAC=90 độ
DO đó: ABEC là hình chữ nhật
=>ΔBEC vuông tại E
Đúng 0
Bình luận (0)
Bài 1 : giải phương trình
a,\(\sqrt{x^2-x+9}=x+2\)
b,\(\sqrt{x+13}=x+1\)
c,\(\sqrt{2x+1}+\sqrt{x-3}=4\)
d,\(\sqrt{x-2}+\sqrt{4-x}=x^2-6x+11\)
e,\(x^2-5x+30=4\sqrt{x}-6\sqrt{2x+1}\)
a: \(\Leftrightarrow\left\{{}\begin{matrix}x>=-2\\x^2+4x+4-x^2+x-9=0\end{matrix}\right.\Leftrightarrow x=1\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}x>=-1\\x^2+2x+1=x+13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-1\\x^2+x-12=0\end{matrix}\right.\)
=>x=3
Đúng 0
Bình luận (0)
Bài 11. Cho LABC có AB = AC và M là trung điểm của BC a) Chung minh AAMB = AAMC b) Qua A và a i AM Chứng minh AM LBC và BC c) Qua C, vẽ b//AM. Gọi N là giao điểm của hai đường thẳng a và b. Chứng minh AAMC=ACNA d) Gọi I là trung điểm của đoạn AC. Chứng minh I là trung điểm của đoạn MN
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
c:
Xét tứ giác AMCN có
AM//CN
AN//CM
góc AMC=90 độ
=>AMCN là hình chữ nhật
Xét ΔAMC vuông tại M và ΔCNA vuông tại N có
AC chung
AM=CN
=>ΔAMC=ΔCNA
d: AMCN là hình chữ nhật
=>AC cắt MN tại trung điểm của mỗi đường
mà I là trung điểm của AC
nên I là trung điểm của MN
Đúng 0
Bình luận (0)
Bài 4 : Vẽ hình : Cho tam giác ABC. Trên tia đối của AC lấy điểm D sao cho AD = AC. Trên tia đối của AB lấy điểm E sao cho AE = AB. Chứng minh rằng :
a) BC \(//\) DE
b) Một đường thẳng đi qua A cắt các cạnh DE và BC theo thứ tự tại M và N. Chứng minh rằng : AM = AN ; DM = CN
a: Xét tứ giác BDEC có
A là trung điểm chung của BE và DC
nên BDEC là hình bình hành
Suy ra: BC//DE; BC=DE
b: Xét ΔADM và ΔACN có
góc DAM=góc CAN
AD=AC
góc ADM=góc ACN
Do đó: ΔADM=ΔACN
Suy ra: AM=AN; DM=CN
Đúng 0
Bình luận (0)
Bài 3 : Vẽ hình : Cho hai đoạn thẳng AB và Cd cắt nhau tại trung điểm O của mỗi đường.
a) Chứng minh rằng : \(\Delta AOD=\Delta BOC\)
b) Lấy điểm \(I\) thuộc đoạn AD, điểm K thuộc đoạn BC sao cho AI = BK. Chứng minh rằng : O là trung điểm của IK
a: Xét ΔAOD và ΔBOC có
OA=OB
góc AOD=góc BOC
OD=OC
Do đó: ΔAOD=ΔBOC
b: Xét tứ giác AIBK có
AI//BK
AI=BK
Do đó: AIBK là hình bình hành
Suy ra:AB cắt IK tại trung điểm của mỗi đường
=>O là trung điểm của IK
Đúng 0
Bình luận (0)
Cho hai tam giác bằng nhau: tam giác A',B',C' có 3 đỉnh. Hãy viết kí hiệu về sự bằng nhau của tam giác đó biết: AB=B'C', AC=B'A',BC=C'A'?
Xem chi tiết
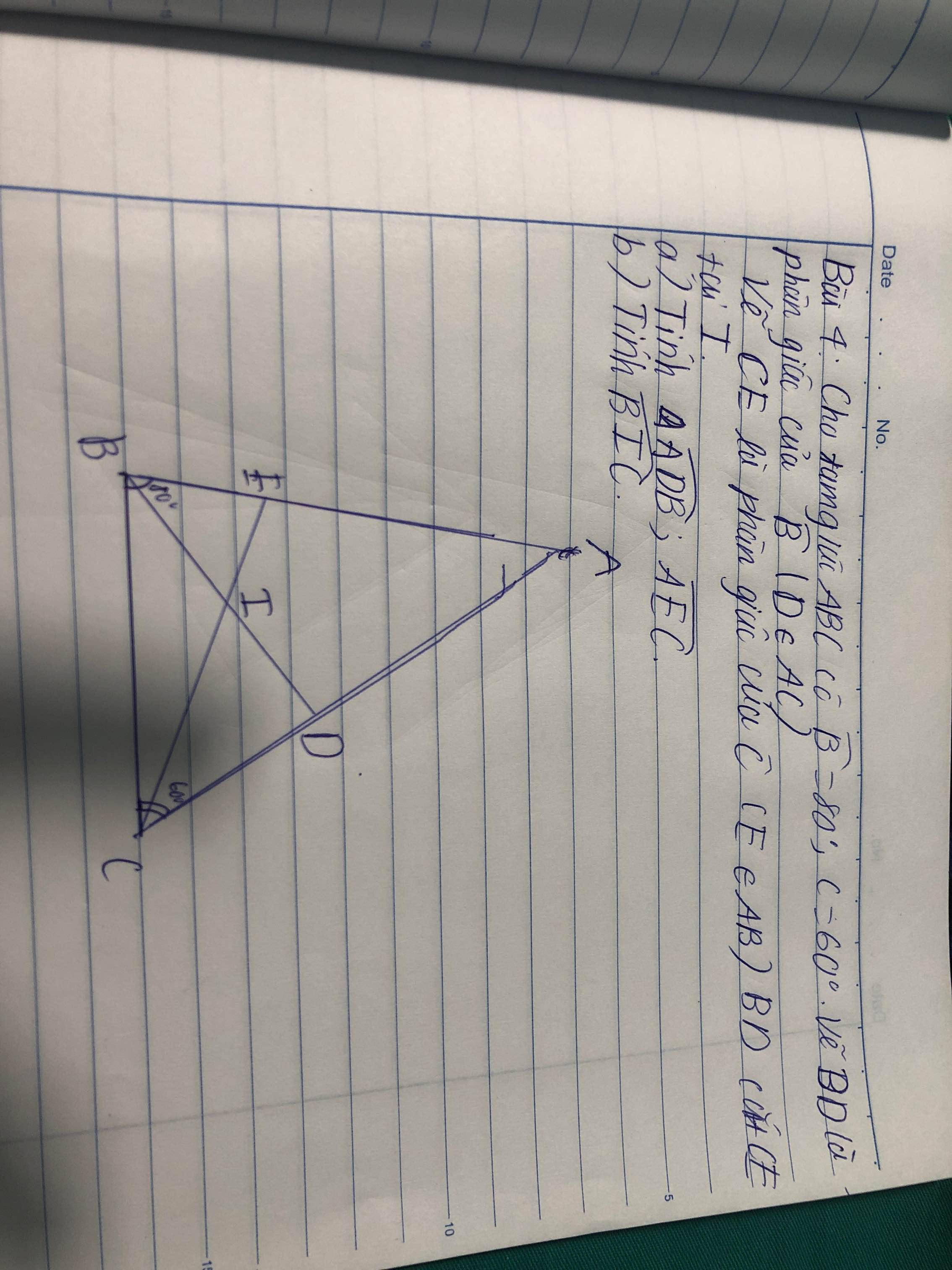
mn giúp em bài này với ạ e đag càn gấpppp
a)Xét tam giác ABC có:
A + B + C = 180 =>A = 180 -60 - 80 = 40
ABD = 40 vì BD là p giác
Xét tam giác ADB có :
BAD + ABD + ADB = 180 => ADB = 180 - 40 -40 = 100
Đúng 1
Bình luận (0)
a) ta có ACE = 30 vì CE là phân giác góc C
Xét tam giác AEC có :
AEC + ACE + CAE = 180 => AEC = 180 - 30 - 40= 110
Đúng 1
Bình luận (0)
b) Ta có : IBC = 40
ICB = 30
Xét tam giác IBC có :
IBC + ICB + BIC = 180
=> BIC = 180 - 30 -40 = 110
Đúng 1
Bình luận (1)
8:
góc MBC+góc MCB=90/2=45 độ
=>góc BMC=135 độ
Đúng 0
Bình luận (0)