cho tam giác ABC= tam giác DMN. biết BC=6 cm, B= 60 độ, AC=4cm. a) tam giác DMN có góc nào cũng có số đo bằng 60 độ b) suy ra số đo cạnh nào của tam giác DMN
Bài 2: Hai tam giác bằng nhau
a) Ta có: \(\Delta ABC=\Delta DMN\left(gt\right)\)
Mà: \(\widehat{B}=60^o\)
\(\Rightarrow\widehat{M}=60^o\)
b) \(BC=6\left(cm\right)\)
\(\Rightarrow MN=6\left(cm\right)\)
\(AC=4\left(cm\right)\)
\(\Rightarrow DN=4\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy M , trên tia đối của CB lấy N sao cho BM = CN
a) CM : tam giác AMN cân
b. kẻ BE vuông góc AM (E thuộc AM),CF vuông góc AN . CM:tam giác BME= tam giác CNF
c.EB cắt FC tại O. CM: AO là phân giác của góc MAN
d.qua M kẻ vuông góc AM,qua N kẻ vuông góc AN 2 đường thẳng cắt nhau tại H . CM: A , O , H thẳng hàng
a: Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góckề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
b: Xét ΔBME vuông tại E và ΔCNF vuông tại F có
BM=CN
\(\widehat{BME}=\widehat{CNF}\)(ΔABM=ΔACN)
Do đó: ΔBME=ΔCNF
c: Ta có: ΔBME=ΔCNF
=>ME=NF
Ta có: AE+EM=AM
AF+FN=AN
mà AM=AN và ME=NF
nên AE=AF
Xét ΔAEO vuông tại E và ΔAFO vuông tại F có
AO chung
AE=AF
Do đó: ΔAEO=ΔAFO
=>\(\widehat{EAO}=\widehat{FAO}\)
=>\(\widehat{MAO}=\widehat{NAO}\)
=>AO là phân giác của góc MAN
d: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
AM=AN
Do đó: ΔAMH=ΔANH
=>\(\widehat{MAH}=\widehat{NAH}\)
=>AH là phân giác của góc MAN
mà AO là phân giác của góc MAN
nên A,O,H thẳng hàng
Đúng 1
Bình luận (0)
cho tam giác ABC (AB>AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD. a) Chứng minh tam giác ACM= tam giác DBM. b) Kẻ BE vuông góc với AM tại E. Trên tia MD lấy điểm F sao cho M là trung điểm của EF. Chứng minh CF vuông góc với AD. c) Trên tia FB lấy điểm G sao cho B là trung điểm FG. Gọi H là trung điểm của BE. Chứng minh ba điểm G,H,C thẳng hàng
a: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
b: Xét ΔMEB và ΔMFC có
ME=MF
\(\widehat{BME}=\widehat{CMF}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMEB=ΔMFC
=>\(\widehat{MEB}=\widehat{MFC}\)
=>\(\widehat{MFC}=90^0\)
=>CF\(\perp\)AD
c: Xét tứ giác BFCE có
M là trung điểm chung của BC và FE
=>BFCE là hình bình hành
=>BF//CE và BF=CE
Ta có: BF//CE
B\(\in\)FG
Do đó: BG//CE
Ta có: BF=CE
BF=BG
Do đó: BG=CE
Xét tứ giác BGEC có
BG//EC
BG=EC
Do đó: BGEC là hình bình hành
=>BE cắt GC tại trung điểm của mỗi đường
mà H là trung điểm của BE
nên H là trung điểm của GC
=>G,H,C thẳng hàng
Đúng 1
Bình luận (0)
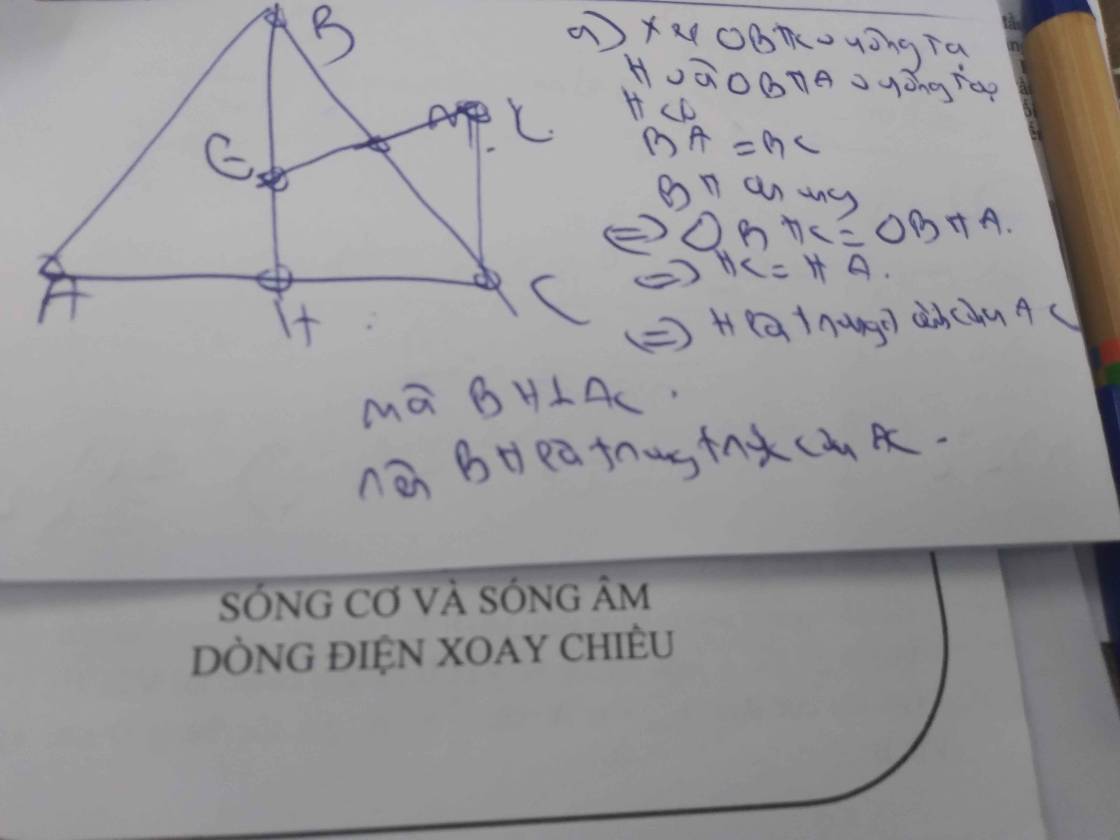
Cho Tam giác ABC cân tại A ,trên tia dối của tia CA lấy N sao cho CN =CA ,Trên tia đối của tia CB lấy M sao chO CM=CB kẻ AH vuông góc với BC,NK vuông góc với BC a) chứng minh AB//MN b) chứng minh tam giác ABH=tam giác NCK
a: Xét ΔCAB và ΔCNM có
CA=CN
\(\widehat{ACB}=\widehat{NCM}\)(hai góc đối đỉnh)
CB=CM
Do đó: ΔCAB=ΔCNM
=>\(\widehat{CAB}=\widehat{CNM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//MN
b:
Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC
Xét ΔHAC vuông tại H và ΔKNC vuông tại K có
AC=NC
\(\widehat{HCA}=\widehat{KCN}\)(hai góc đối đỉnh)
Do đó: ΔHAC=ΔKNC
=>HC=KC
mà HB=HC
nên HB=KC
Xét ΔABH vuông tại H và ΔNCK vuông tại K có
BH=CK
\(\widehat{ABH}=\widehat{NCK}\)\(\left(=\widehat{ACB}\right)\)
Do đó: ΔABH=ΔNCK
Đúng 1
Bình luận (0)
 chi tiết vẽ hình càng tốt
chi tiết vẽ hình càng tốt
Cho tam giác ABC cân tại A . Gọi M là một điểm nằm trong tam giác sao cho MB=MC. N là trung điểm của BC . Chứng minh rằng
A) AM là tia phân giác của góc BAC
B) MN là đường trung trực của đoạn BC.
C) Ba điểm A,M,N thẳng hàng
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
=>AM là phân giác của góc BAC
b: MB=MC
NB=NC
=>MN là trung trực của BC(1)
c: AB=AC
=>A nằm trên trung trực của BC(2)
Từ (1), (2) suy ra A,M,N thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên cạnh AB,AC lấy lần lượt 2 điểm H và K sao cho AH=AK. Gọi giao điểm của CH và BK là O. Chứng minh
a)CH=BK
b)tam giác HOB = tam giác KOC
c)gọi I là giao điểm của AO và BC. So sánh độ dài cạnh AB và AI
a: Xét ΔAKB và ΔAHC có
AK=AH
góc BAK chung
AB=AC
=>ΔAKB=ΔAHC
=>CH=BK
b: Xét ΔOHB và ΔOKC có
góc OHB=góc OKC
HB=KC
góc OBH=góc OCK
=>ΔOHB=ΔOKC
c: ΔOHB=ΔOKC
=>OB=OC
=>AO là trung trực của BC
=>AO vuông góc BC tại I
=>AB>AI
Đúng 0
Bình luận (0)
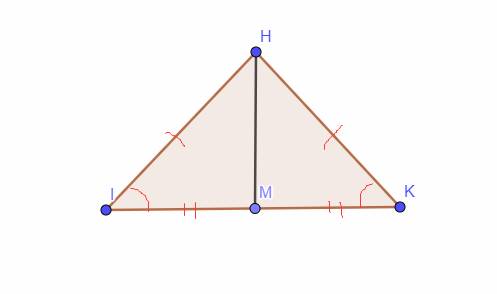
Cho tam giác HIK có HI=HK.Gọi M là trung điểm của IK.Chứng minh tam giác HIM=tam giác HKM
Vì Tam giác `HIK` có `HI = HK`
`-> \text {Tam giác HIK cân tại H} ->`\(\widehat{I}=\widehat{K}\)
Xét Tam giác `HIM` và Tam giác `HKM` có:
`HI=HK (g``t)`
\(\widehat{I}=\widehat{K}\) `(CMT)`
`MI=MK (` vì `M` là trung điểm của `IK)`
`=> \text {Tam giác HIM = Tam giác HKM (c-g-c)}`
Đúng 1
Bình luận (1)
cho tam giác ABC vuông tại A vẽ BK là phân giác của B (K thuộc AC) Gọi H là chân đường vuông góc tuef A đến BK;AH cắt BC tại E a chứng minh tam giác BHA= tam giác BHE b chúng minh KE vuông góc BC
a: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
góc HBA=góc HBE
=>ΔBHA=ΔBHE
b: Xét ΔBAK và ΔBEK có
BA=BE
góc ABK=góc EBK
BK chung
=>ΔBAK=ΔBEK
=>góc BEK=90 độ
=>KE vuông góc BC
Đúng 0
Bình luận (0)