Bài 5: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
Nội dung lý thuyết
Các phiên bản khác1. Vẽ tam giác biết một cạnh và hai góc kề
Bài toán: Vẽ tam giác \(ABC\) biết \(BC=4cm\), \(\widehat{B}=60^0\), \(\widehat{C}=40^0\)
Các bước làm:
- Vẽ đoạn thẳng \(BC=4cm\)
- Trên cùng một nửa mặt phẳng bờ \(BC\) vẽ các tia \(Bx\), \(Cy\) sao cho \(\widehat{CBx}=60^0\), \(\widehat{BCy}=40^0\)
- Hai tia trên cắt nhau tại \(A\). Ta được tam giác \(ABC\) thoả mãn yêu cầu bài toán.
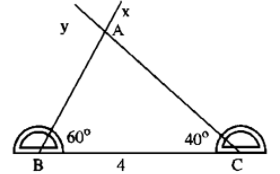
Lưu ý: Ta gọi góc \(B\) và góc \(C\) là hai góc kề cạnh \(BC\).
Khi nói một cạnh và hai góc kề, ta hiểu hai góc này là hai góc ở vị trí kề cạnh đó.
Ví dụ: góc \(A\) và góc \(B\) là hai góc kề cạnh \(AB\) ; góc \(A\) và góc \(C\) là hai góc kề cạnh \(AC\).
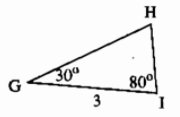
Tương tự như vậy: Vẽ tam giác \(GHI\) có \(GI=3cm\), \(\widehat{G}=30^0\), \(\widehat{I}=80^0\).
- Vẽ đoạn thẳng \(GI=3cm\)
- Trên cùng một nửa mặt phẳng bờ \(GI\), vẽ một tia \(Gx\) sao cho \(\widehat{IGx}=30^0\) và tia \(Ix'\) sao cho \(\widehat{GIx'}=80^0\).
- Hai tia \(Gx\) và \(Ix'\) cắt nhau tại \(H\). Ta được tam giác \(GHI\) thoả mãn yêu cầu bài toán.
* Trong trường hợp bài toán cho một cạnh và hai góc nhưng có một góc không phải là góc kề cạnh đó, ta có thể dùng tính chất "Tổng ba góc trong một tam giác bằng \(180^0\)" để tìm ra góc còn lại là góc kề cạnh đã cho.
Ví dụ: Vẽ tam giác \(DEF\) biết cạnh \(DE=6,5cm\), \(\widehat{D}=35^0\), \(\widehat{F}=100^0\)?
Vì đã biết cạnh \(DE\) nên ta cần hai góc kề cạnh đó là góc \(\widehat{D}\)và góc \(\widehat{E}\).
Áp dụng tính chất về tổng ba góc trong một tam giác ta được: \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{E}=180^0-\widehat{D}-\widehat{F}=180^0-35^0-100^0=45^0\).
Khi đó ta vẽ tam giác \(DEF\) có \(DE=6,5cm\), \(\widehat{D}=35^0\), \(\widehat{E}=45^0\) tương tự như cách vẽ tam giác \(ABC\) và tam giác \(GHI\) trên.
2. Trường hợp bằng nhau thứ ba góc - cạnh - góc
Ta thừa nhận tính chất cơ bản sau:
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
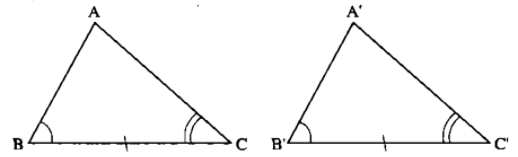
Ví dụ 1: Nếu \(\Delta ABC\) và \(\Delta A'B'C'\) có
\(\widehat{B}=\widehat{B'}\)
\(BC=B'C'\)
\(\widehat{C}=\widehat{C'}\)
thì \(\Delta ABC=\Delta A'B'C'\) (g.c.g)
Ví dụ 2: Nếu \(\Delta MNP\) và \(\Delta EFQ\) có:
\(\widehat{M}=\widehat{E}\)
\(MN=EF\)
\(\widehat{N}=\widehat{F}\)
thì \(\Delta MNP=\Delta EFQ\) (g.c.g)
Bài tập ví dụ: Cho tam giác \(ABC\) có \(AB=AC\); \(\widehat{B}=\widehat{C}\), \(AD\) là tia phân giác góc \(\widehat{A}\) (\(D\in BC\)). Chứng minh \(DB=DC\)?
Giải:
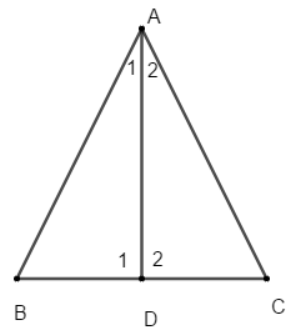
Do \(AD\) là tia phân giác của góc \(\widehat{A}\) \(\Rightarrow\) \(\widehat{A_1}=\widehat{A_2}=\dfrac{1}{2}\widehat{BAC}\)
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(\widehat{A_1}=\widehat{A_2}\)
\(AB=AC\) (gt)
\(\widehat{B}=\widehat{C}\) (gt)
\(\Rightarrow\) \(\Delta ABD=\Delta ACD\) (g.c.g)
\(\Rightarrow\) \(DB=DC\) (hai cạnh tương ứng) (Đpcm)
@54477@
3. Hệ quả
Hệ quả 1:
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Tam giác \(ABC\) vuông tại \(A\) và tam giác \(DEF\) vuông tại \(E\) có \(AC=EF\); \(\widehat{C}=\widehat{F}\)(hình vẽ)
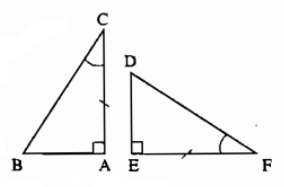
Ta dễ dàng chứng minh được \(\Delta ABC=\Delta EDF\) (g.c.g)
Hệ quả 2:
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Xét hai tam giác \(ABC\) vuông tại \(A\) và tam giác \(DEF\) vuông tại \(D\) có \(BC=EF\), \(\widehat{B}=\widehat{E}\):
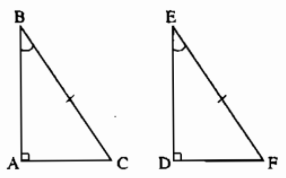
Ta có: Trong một tam giác vuông, hai góc nhọn phụ nhau
\(\Rightarrow\widehat{C}=90^0-\widehat{B}\) ; \(\widehat{F}=90^0-\widehat{E}\) mà \(\widehat{B}=\widehat{E}\) (gt)
\(\Rightarrow\) \(\widehat{C}=\widehat{F}\)
Từ đó suy ra \(\Delta ABC=\Delta DEF\) (g.c.g)
@1348819@