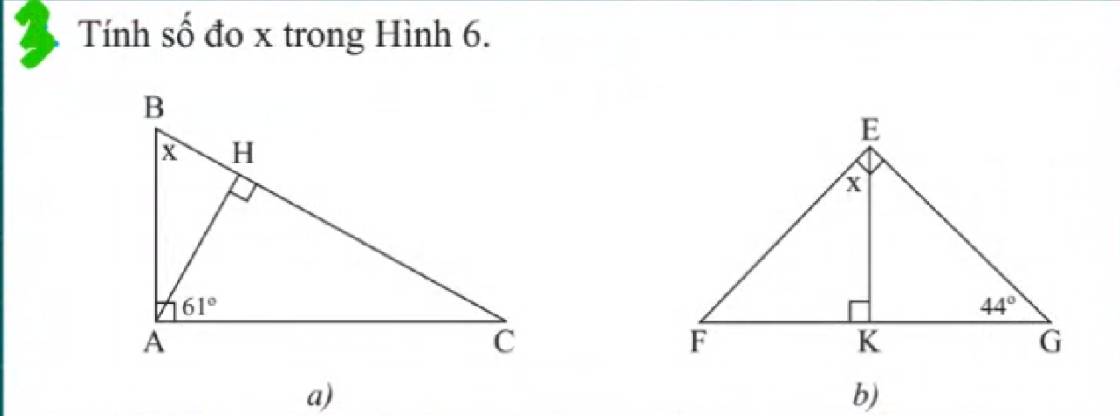
Cho ta giác ABC có AB<AC. Vẽ BD vuông góc AC tại D và CE vuông góc AB tại E, BD cắt CE ở I. BIC kề bù với góc nào? Giải thích?
Bài 1: Tổng ba góc của một tam giác
Xét tứ giác AEID có
\(\widehat{AEI}+\widehat{ADI}+\widehat{EAD}+\widehat{EID}=360^0\)
=>\(\widehat{EAD}+\widehat{EID}+90^0+90^0=360^0\)
=>\(\widehat{EAD}+\widehat{EID}=360^0-180^0=180^0\)
mà \(\widehat{EID}=\widehat{BIC}\)(hai góc đối đỉnh)
nên \(\widehat{EAD}+\widehat{BIC}=180^0\)
=>góc BIC bù với góc BAC
Đúng 1
Bình luận (0)
Cho tam giác ABC=DEF BIẾT B=50 ĐỘ D=70 ĐỘ.TÍNH SỐ ĐO GÓC C
Do ∆ABC = ∆DEF (gt)
⇒ ∠A = ∠D = 70⁰
∆ABC có:
∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ABC)
⇒ ∠C = 180⁰ - (∠A + ∠B)
= 180⁰ - (70⁰ + 50⁰)
= 60⁰
Đúng 3
Bình luận (0)
ΔABC=ΔDEF
=>\(\widehat{A}=\widehat{D}=70^0\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{C}+70^0+50^0=180^0\)
=>\(\widehat{C}=180^0-120^0=60^0\)
Đúng 2
Bình luận (0)
Có: \(\Delta ABC=\Delta DEF\)
\(\Rightarrow\widehat{A}=\widehat{ D}\) (hai góc tương ứng)
Mà: \(\widehat{D}=70^o\)
nên \(\widehat{A}=70^o\)
Xét \(\Delta ABC\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) (định lí tổng các góc trong tam giác)
\(\Rightarrow70^o+50^o+\widehat{C}=180^o\) (vì \(\widehat{A}=70^o;\widehat{B}=50^o\))
\(\Rightarrow120^o+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=180^o-120^o=60^o\)
Vậy: \(\widehat{C}=60^o\).
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC tại mỗi đingr vẻ một góc ngoài của tam giác tính tổng số đo 3 góc ngoài
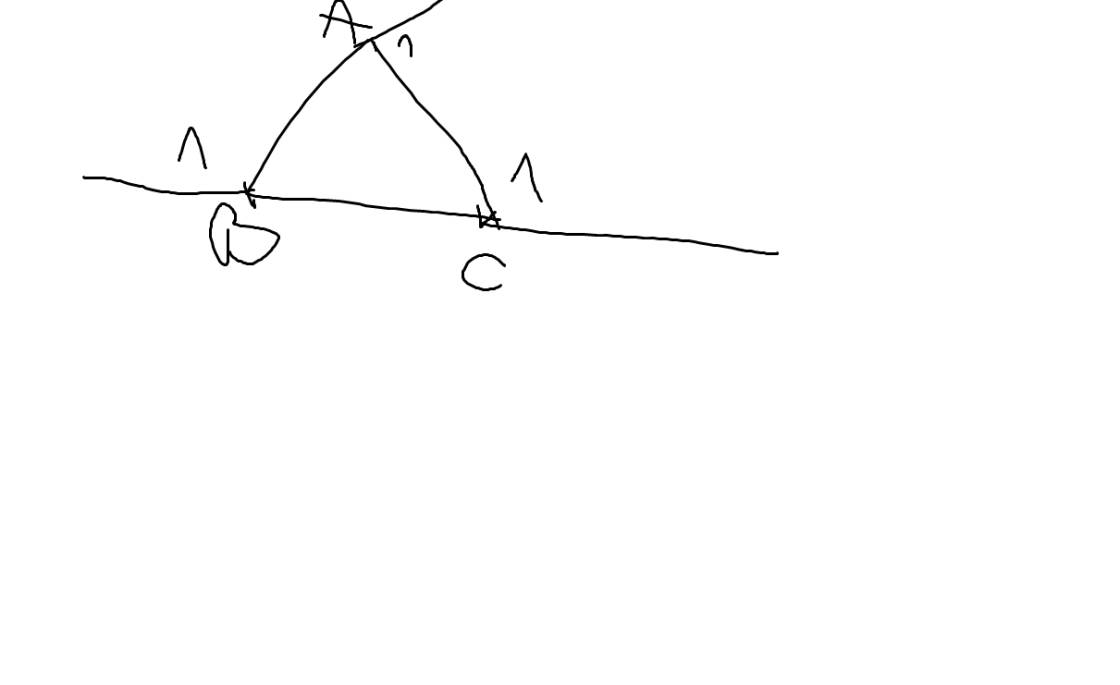
Gọi \(\widehat{A_1};\widehat{B_1};\widehat{C_1}\) lần lượt là các góc ngoài tại các đỉnh A,B,C của ΔABC
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\widehat{B_1}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}=180^0-\widehat{ABC}\)
\(\widehat{C_1}+\widehat{ACB}=180^0\)(hai góc kề bù)
=>\(\widehat{C_1}=180^0-\widehat{ACB}\)
\(\widehat{A_1}+\widehat{BAC}=180^0\)(hai góc kề bù)
=>\(\widehat{A_1}=180^0-\widehat{BAC}\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}\)
\(=180^0-\widehat{BAC}+180^0-\widehat{ABC}+180^0-\widehat{ACB}\)
\(=540^0-180^0=360^0\)
Đúng 1
Bình luận (0)
Bài 4: Cho một tam giác vuông có hai góc nhọn bằng nhau. Tính mỗi góc nhọn đó. Bài 5: Tính các góc của ABC, biết: A^-B^ 18* và B^ - C^ 18*
Đọc tiếp
Bài 4: Cho một tam giác vuông có hai góc nhọn bằng nhau. Tính mỗi góc nhọn đó.
Bài 5: Tính các góc của ![]() ABC, biết: A^-B^ = 18* và B^ - C^ =18*
ABC, biết: A^-B^ = 18* và B^ - C^ =18*
4:
Trong một tam giác vuông thì hai góc nhọn có tổng số đo là 90 độ
mà hai góc nhọn đó bằng nhau
nên số đo của mỗi góc nhọn là: \(\dfrac{90}{2}=45^0\)
5:
Đặt \(\widehat{A}=a;\widehat{B}=b;\widehat{C}=c\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=18\\b-c=18\\a+b+c=180\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b+18\\c=b-18\\a+b+c=180\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=b+18\\c=b-18\\b+18+b+b-18=180\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=60\\a=78\\c=42\end{matrix}\right.\)
=>\(\widehat{A}=78^0;\widehat{B}=60^0;\widehat{C}=42^0\)
Đúng 2
Bình luận (0)
A B D C 80độ 30độ Tính góc ADC và góc ADB
Đọc tiếp
Xét tam giác ABC có:
góc A+góc B+góc C = 180 độ
=>góc A = 180 độ -góc B-góc C=180 độ - 80 độ - 30 độ = 100 độ - 30 độ = 70 độ
Vì AD là tia phân giác của góc A
=> Góc BAD=góc CAD= góc A/2=70 độ/2=35 độ
Xét tam giác ABD có:
Góc ABD+ góc BAD + góc ADB=180 độ
=> Góc ADB=180 độ -góc B-góc BAD =180 độ-80 độ-35 độ=100 độ -35 độ=65 độ
Xét tam giác ACD có:
Góc ACD+góc CAD+góc ADC=180 độ
=> Góc ADC=180 độ -góc C-góc CAD=180 độ-30 độ-35 độ=150 độ -35 độ=115 độ
Vậy góc ADB = 65 độ
góc ADC = 115 độ
Đúng 1
Bình luận (0)
25độ x A E D B C vuông vuông Cho hình vẽ tìm x
Đọc tiếp
Gọi giao điểm của EC và BD là K
Xét \(\Delta DKC\) có:
\(\widehat{KDC}+\widehat{DCK}+\widehat{DKC}=180^o\)
\(\Rightarrow90^o+25^o+\widehat{DKC}=180^o\)
\(\Rightarrow\widehat{DKC}=180^o-90^o-25^o\)
\(\Rightarrow\widehat{DKC}=65^o\)
mà \(\widehat{CKD}=\widehat{BKE=65^o}\) (2 góc đối đỉnh)
Xét \(\Delta EKB\) có:
\(\widehat{KEB}+\widehat{EKB}+\widehat{EBK}=180^o\)
\(\Rightarrow90^o+65^o+x=180^o\)
\(\Rightarrow x=180^o-90^o-65^o\)
\(\Rightarrow x=25^o\)
Đúng 5
Bình luận (0)
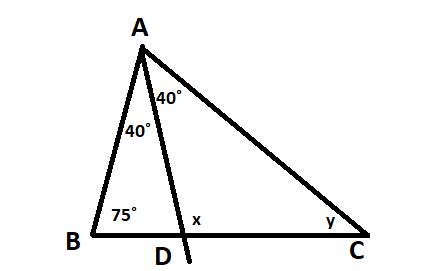 Tính số đo x và y
Tính số đo x và y
x=70+45=115 độ
y=180-80-75=100-75=25 độ
Đúng 0
Bình luận (0)
Xét tam giác ABD ta có:
\(\widehat{BAD}+\widehat{B}+\widehat{BDA}=180^o\)
\(\Rightarrow\widehat{BDA}=180^o-\widehat{BAD}-\widehat{B}=180^o-75^o-40^o=65^o\)
Mà: \(\widehat{BDA}+\widehat{ADC}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{ADC}=x=180^o-\widehat{BDA}=180^o-65^o=115^o\)
Xét tam giác ABC ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\left(\widehat{BAD}+\widehat{DAC}\right)+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=y=180^o-\left(40^o+40^o\right)-75^o=25^o\)
Đúng 1
Bình luận (0)
\(\widehat{D}=180-\widehat{A1}-\widehat{B}=65^o\)
mà \(\widehat{x}\) kề bù \(\widehat{D}\) =>góc x=180-góc D=115độ
góc y = 180 - góc A2 - góc x = 25 độ
Đúng 1
Bình luận (0)
Tam giác ABC vuông tại B có A^ = 3C^. Tính số đo của góc A
Ta có:
\(\widehat{A}+\widehat{C}=90^o\)(Phụ nhau)
Mà \(\widehat{A}=3\widehat{C}\)
\(\Rightarrow3\widehat{C}+\widehat{C}=90^o\)
\(\Rightarrow4\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}=22,5^o\)
\(\Rightarrow\widehat{A}=22,5^o\times3=67,5^o\)
Đúng 0
Bình luận (0)
Cho góc xoy khác góc bẹt.Trên cạch ox lấy hai điểm A và B,trên cạnh oy lấy hai điểm C và D,sao cho OA=OC,OB=OD a)Chứng minh tam giác OAD=tam giácOAB b)Chứng minh tam giác ACD=tam giácCAB
Sửa `a)` CM tam giác OAD=tam giác OCB
`a)`
Xét `Delta OAD` và `Delta OCB` có :
`{:(OD=OB(GT)),(hat(O)-chung),(OA=OC(GT)):}}`
`=>Delta OAD=Delta OCB(c.g.c)(đpcm)`
`b)`
`Delta OAD=Delta OCB(cmt)=>hat(D_1)=hat(B_1)` ( 2 góc t/ứng )
Có `OC=OA;OB=OD(GT)`
`=>OB-OA=OD-OC`
hay `AB=CD`
Có `OC=OA(GT)`
`=>Delta OAC` cân tại `O`
`=>hat(C_1)=hat(A_1)`
mà `hat(C_1)+hat(ACD)=180^0` ( kề bù )
`hat(A_1)+hat(CAB)=180^0` ( kề bù )
nên `hat(ACD)=hat(CAB)`
Xét `Delta ACD` và `Delta CAB` có :
`{:(hat(D_1)=hat(B_1)(cmt)),(CD=AB(cmt)),(hat(ACD)=hat(CAB)(cmt)):}}`
`=>Delta ACD=Delta CAB(c.g.c)(đpcm)`
Đúng 2
Bình luận (0)
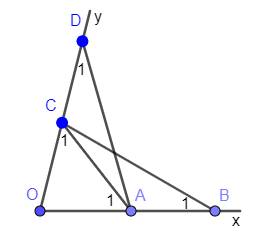
a, Ta có: \(\widehat{BAC}=90^o\)
Mà \(\widehat{HAC}=61^o\)
\(\Rightarrow\widehat{BAH}=\widehat{BAC}-\widehat{HAC}=90^o-61^o=29^o.\)
Xét △BAH vuông tại H có:
\(\widehat{BAH}+\widehat{BHA}+\widehat{ABH}=180^o\) ( Tổng 3 góc trong △ )
Mà \(\widehat{BAH}=29^o\)
\(\widehat{BHA=90^o}\)
\(\Rightarrow\widehat{ABH}=180^o-\widehat{BAH}-\widehat{BHA}=180^o-29^o-90^o=61^o.\)
b, Xét △KEG vuông tại K có:
\(\widehat{GEK}+\widehat{EKG}+\widehat{EGK}=180^o\left(t3g\Delta\right)\)
Mà \(\widehat{EGK}=44^o\)
\(\widehat{EKG}=90^o\)
\(\Rightarrow\widehat{GEK}=180^o-90^o-44^o=46^o\)
Ta có: \(\widehat{FEG}-90^o\)
Mà \(\widehat{GEK}=46^o\)
\(\Rightarrow\widehat{FEK}=90^o-46^o=44^o.\)
Đúng 3
Bình luận (1)
a: x=góc HAC=61 độ
b: x=góc G=44 độ
Đúng 0
Bình luận (0)