Bài 1: Tổng ba góc của một tam giác

1. Tổng ba góc của một tam giác

Định lí:

Tổng ba góc trong một tam giác bằng \(180^0\).

Chứng minh định lí:

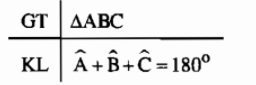
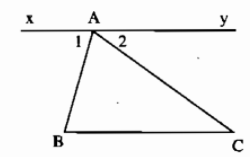
Qua \(A\) kẻ đường thẳng \(xy\) // \(BC\)

Khi đó ta có  \(\widehat{A_1}=\widehat{B}\) (hai góc so le trong) và \(\widehat{A_2}=\widehat{C}\) (hai góc so le trong)

Ta có \(\widehat{BAC}+\widehat{A_1}+\widehat{A_2}=180^0\) \(\Rightarrow\widehat{BAC}+\widehat{B}+\widehat{C}=180^0\). Đây là điều phải chứng minh.

Xét ví dụ sau:

Cho tam giác \(ABC\) biết \(\widehat{B}=87^0\), \(\widehat{C}=67^0\). Tính số đo góc \(\widehat{A}\)?

Bài giải:

Áp dụng định lí tổng ba góc trong một tam giác ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

\(\Rightarrow\widehat{A}=180^0-\widehat{B}-\widehat{C}=180^0-87^0-67^0=26^0\)

Vậy \(\widehat{A}=26^0\).

2. Áp dụng vào tam giác vuông

Định nghĩa:

Tam giác vuông là tam giác có một góc vuông.

Định lí:

Trong một tam giác vuông, hai góc nhọn phụ nhau.

 Ví dụ: Xét tam giác \(ABC\) vuông tại \(A\):

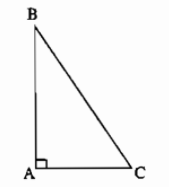
Áp dụng định lí tổng ba góc trong một tam giác ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) 

\(\Rightarrow\) \(\widehat{B}+\widehat{C}=180^0-\widehat{A}\) \(\Rightarrow\widehat{B}+\widehat{C}=180^0-90^0\) (do tam giác \(ABC\) vuông tại \(A\))

\(\Rightarrow\) \(\Rightarrow\widehat{B}+\widehat{C}=90^0\)

Xét ví dụ: Cho tam giác \(ABC\) vuông tại \(A\), biết \(\widehat{B}=2\widehat{C}\). Tính \(\widehat{B}\)?

Bài giải:

Áp dụng định lí "Trong một tam giác vuông, hai góc nhọn phụ nhau" ta có \(\widehat{B}+\widehat{C}=90^0\)

Lại có: \(\widehat{B}=2\widehat{C}\) \(\Rightarrow\dfrac{\widehat{B}}{1}=\dfrac{\widehat{C}}{2}=\dfrac{\widehat{B}+\widehat{C}}{1+2}=\dfrac{90^0}{3}=30^0\)

Vậy \(\widehat{B}=30^0\).

3. Góc ngoài của tam giác

Định nghĩa:

Góc ngoài của tam giác là góc kè bù với một góc của tam giác đó.

Định lí:

Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó.

Nhận xét: Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó.

Ví dụ: Cho tam giác \(ABC\), kéo dài \(BC\) được tia \(Bx\). Khi đó \(\widehat{ACx}\) là góc ngoài đỉnh \(C\) của tam giác \(ABC\).

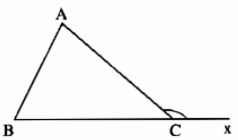
Ta có: \(\widehat{ACx}=\widehat{A}+\widehat{B}\)

Và \(\widehat{ACx}>\widehat{A}\), \(\widehat{ACx}>\widehat{B}\).