Bài 4: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)

1. Vẽ tam giác biết hai cạnh và góc xen giữa

Bài toán: Vẽ tam giác \(ABC\) biết \(AB=2cm\), \(BC=3cm\), \(\widehat{B}=70^0\).

Giải:

- Vẽ góc  \(\widehat{xBy}=70^0\).

- Trên \(Bx\) lấy \(A\) sao cho \(BA=2cm\).

- Trên \(By\) lấy \(C\) sao cho \(BC=3cm\).

- Vẽ đoạn thẳng \(AC\),  ta được \(\Delta ABC\) thoả mãn yêu cầu.

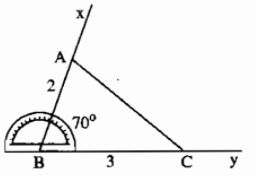
Lưu ý: Trong bài toán trên, ta biết cạnh \(AB\), cạnh \(BC\) và góc \(\widehat{B}\) là góc xen giữa 2 cạnh \(AB\) và \(BC\).

Khi nói hai cạnh và góc xen giữa, ta hiểu góc này là góc ở vị trí xen giữa hai cạnh đó.

Tương tự như vậy:

- Xét trong tam giác \(ABC\):

+) Góc \(\widehat{C}\) là góc xen giữa hai cạnh \(AC,BC\).

+) Góc \(\widehat{A}\) là góc xen giữa hai cạnh \(AB,AC\).

- Xét trong tam giác \(HIK\):

+) Góc \(\widehat{H}\) là góc xen giữa hai cạnh \(HI,HK\)

+) Góc \(\widehat{I}\) là góc xen giữa hai cạnh \(HI,IK\)

+) Góc \(\widehat{K}\) là góc xen giữ hai cạnh \(HK,IK\)

2. Trường hợp bằng nhau cạnh - góc - cạnh

Tính chất:

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

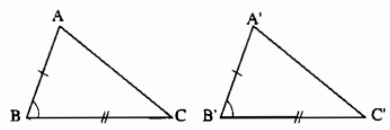
Ví dụ 1: Nếu tam giác \(ABC\) và tam giác \(A'B'C'\) có:

\(AB=A'B'\)

\(\widehat{B}=\widehat{B'}\)

\(BC=B'C'\)

thì \(\Delta ABC=\Delta A'B'C'\) (c.g.c) (hình minh hoạ)

Ví dụ 2: Nếu tam giác \(DEF\) và tam giác \(MNP\) có:

\(DE=MN\)

\(\widehat{D}=\widehat{M}\)

\(DF=MP\)

thì \(\Delta DEF=\Delta MNP\) (c.g.c)

Xét bài tập ví dụ sau: Cho tam giác \(DEF\) và tam giác \(MNP\) có \(DE=MN\), \(\widehat{E}=\widehat{N}\), \(EF=NP\). Biết \(\widehat{D}=100^0\), \(\widehat{N}=30^0\). Tính góc \(\widehat{P}\)?

Giải:

Xét \(\Delta DEF\) và \(\Delta MNP\) có:

\(DE=MN\) (gt)

\(\widehat{E}=\widehat{N}\) (gt)

\(EF=NP\) (gt)

\(\Rightarrow\) \(\Delta DEF=\Delta MNP\) (c.g.c)

Khi đó: \(\widehat{D}=\widehat{M}=100^0\) ; \(\widehat{E}=\widehat{N}=30^0\), \(\widehat{F}=\widehat{P}\) (các góc tương ứng bằng nhau)

Xét trong \(\Delta MNP\) có: \(\widehat{M}+\widehat{N}+\widehat{P}=180^0\) 

\(\Rightarrow\) \(100^0 +30^0+\widehat{P}=180^0\) \(\Rightarrow\widehat{P}=180^0-100^0-30^0=50^0\).

Vậy góc \(\widehat{P}=50^0\).

3. Hệ quả

- Lưu ý: Hệ quả cũng là một định lí, nó được suy ra trực tiếp từ một định lí hoặc một tính chất được thừa nhận.

Ta có hệ quả sau:

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Hệ quả này được suy ra từ tính chất trên nhưng trong một trường hợp đặc biệt là góc xen giữa mà ta nhắc đến là góc vuông.

Ví dụ: Cho hai tam giác vuông \(ABC\) và \(DEF\) (hình vẽ):

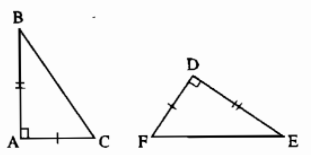
Xét \(\Delta ABC\) và \(\Delta DEF\) có:

\(AB=DE\)

\(\widehat{A}=\widehat{D}=90^0\)

\(AC=DF\)

\(\Rightarrow\Delta ABC=\Delta DEF\) (c.g.c)