Tìm trong các hình 63, 64 các tam giác bằng nhau (các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó ? Viết kí hiệu về sự bằng nhau của các tam giác đó ?
Cho \(\Delta ABC=\Delta HIK\)
a) Tìm cạnh tương ứng với cạnh BC. Tìm góc tương ứng với góc H
b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau
a) Vì \(\Delta ABC=\Delta HIK\)
nên BC = IK (2 cạnh t/ư)
và \(\widehat{A}=\widehat{H}\) (2 góc t/ư)
b) Do \(\Delta ABC=\Delta HIK\)
=> AB = HI; AC = HK (2 cạnh t.ư); BC = IK (câu a)
và \(\widehat{A}=\widehat{H}\) (câu a); \(\widehat{B}=\widehat{I}\) và \(\widehat{C}=\widehat{K}\) (2 góc t/ư).
Trả lời bởi Hoàng Thị Ngọc AnhCho \(\Delta ABC=\Delta HIK\) trong đó \(AB=2cm,\widehat{B}=40^0,BC=4cm\). Em có thể suy ra số đo của những cạnh nào, những góc nào của tam giác HIK ?
Do \(\Delta ABC=\Delta HIK\)
=> AB = HI = 2cm;
\(\widehat{B}=\widehat{I}=40^o\);
\(BC=IK=4cm\)
Trả lời bởi Hoàng Thị Ngọc Anh
Cho \(\Delta ABC=\Delta DEF\). Tính chu vi mỗi tam giác nói trên biết rằng AB = 4cm, BC = 6cm, DF = 5cm (chu vi của một tam giác là tổng độ dài ba cạnh của tam giác đó) ?
Vì \(\Delta ABC=\Delta DEF\)
nên AB = DE = 4cm;
BC = EF = 6cm;
AC = DF = 5cm
Khi đó: \(P_{\Delta ABC}=P_{\Delta DEF}=4+5+6=15\left(cm\right)\)
Vậy \(P_{\Delta ABC}=P_{\Delta DEF}=15cm.\)
Trả lời bởi Hoàng Thị Ngọc AnhCho hai tam giác bằng nhau : tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và một tam giác có 3 đỉnh là H, I, K. Viết kí hiệu về sự bằng nhau của hai tam giác đó biết rằng : \(AB=KI;\widehat{B}=\widehat{K}\)
Ta có \(\widehat{B}=\widehat{K}\) nên B, K là hai đỉnh tương ứng.
AB= KI nên A, I là hai đỉnh tương ứng
vậy \(\Delta\)ABC=\(\Delta\)IKH.
Hai tam giác trong hình 50 có bằng nhau không ? Nếu có, hãy viết kí hiệu sự bằng nhau của hai tam giác đó ?
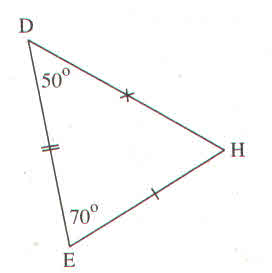
Hình 50
\(\Delta ABC=\Delta EHD\)
Trả lời bởi Nguyen Thuy HoaCho \(\Delta ABC=\Delta DEF\). Viết các cặp cạnh bằng nhau, các cặp góc bằng nhau ?
\(\Delta ABC=\Delta DEF\Rightarrow\widehat{A}=\widehat{D},\widehat{B}=\widehat{E},\widehat{C}=\widehat{F},AB=DE,AC=DF,BC=EF\)
Trả lời bởi Nguyen Thuy HoaCho hai tam giác bằng nhau : tam giác ABC và một tam giác có ba đỉnh là H, K, D. Hãy viết kí hiệu sự bằng nhau của hai tam giác đó, biết rằng AB = KD, \(\widehat{B}=\widehat{K}\)
Trước hết ta xác định B và K là hai đỉnh tương ứng. Sau đó từ AB = KD suy ra A vad D là hai đỉnh tương ứng. Vậy \(\Delta ABC=\Delta DKH\)
Trả lời bởi Nguyen Thuy HoaCho \(\Delta ABC=\Delta DMN\)
a) Viết đẳng thức trên dưới một dạng khác
b) Cho AB = 3cm, AC = 4cm, MN = 6cm. Tính chu vi của mỗi tam giác nói trên ?
Cho \(\Delta ABC=\Delta DEF\). Biết \(\widehat{A}=55^0,\widehat{E}=75^0\)
Tính các góc còn lại của mỗi tam giác ?
Vì \(\Delta ABC=\Delta DEF\) nên \(\widehat{A}\) = \(\widehat{D}\) = \(55^o\)
Ta có : \(\widehat{D}\) + \(\widehat{E}\) + \(\widehat{F}\) = \(180^o\)
\(\widehat{F}\) = \(180^o\) - \(\widehat{D}\) - \(\widehat{E}\)
\(\widehat{F}\) = \(180^o\)- \(55^o\) - \(75^o\)
\(\widehat{F}\) = \(50^o\)
Vì \(\Delta ABC=\Delta DEF\) nên \(\widehat{B}\) = \(\widehat{E}\) = \(75^o\)
Trả lời bởi 阮玉京族
Xem hình a) ta có:
\(\widehat{A}=\widehat{I}=80^0\) ; \(\widehat{C}=\widehat{N}=30^0\)
\(\widehat{B}=\widehat{M}=180^0-\left(80^0+30^0\right)=70^0\)
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
\(\widehat{Q}_2=\widehat{R}_2=80^0\)=800 (ở vị trí so le trong)
Nên QH// RP
Nên \(\widehat{R}_1=\widehat{Q}_1\)= 600(so le trong)
\(\widehat{P}=\widehat{H}\)= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.
Trả lời bởi Lưu Hạ Vy