Bài 2: Hai tam giác bằng nhau

1. Định nghĩa

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Ví dụ: Ta có:  \(AB=A'B'\), \(BC=B'C'\), \(AC=A'C'\), \(\widehat{A}=\widehat{A'}\), \(\widehat{B}=\widehat{B'}\), \(\widehat{C}=\widehat{C'}\). Khi đó tam giác \(ABC\) bằng tam giác \(A'B'C'\) 

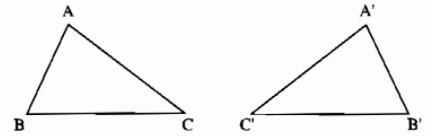
Các cạnh \(AB\) và \(A'B'\), \(BC\) và \(B'C'\), \(AC\) và \(A'C'\) là các cạnh tương ứng. 

Các góc \(\widehat{A}\) và \(\widehat{A'}\) , \(\widehat{B}\) và \(\widehat{B'}\), \(\widehat{C}\) và \(\widehat{C'}\) là các góc tương ứng.

Ví dụ: Cho tam giác \(ABC\) bằng tam giác \(MNP\), Biết \(AB=7cm\), \(MP=10cm\) và chu vi tam giác \(ABC\) là \(24cm\). Tính các cạnh còn lại của mỗi tam giác?

Bài giải:

Tam giác \(ABC\) bằng tam giác \(MNP\) 

\(\Rightarrow\) \(AB=MN=7cm\), \(BC=NP\), \(AC=MP=10cm\).

Chu vi tam giác \(ABC\) là \(24cm\) 

\(\Rightarrow\) \(AB+BC+AC=24cm\) \(\Rightarrow BC=24cm-AB-AC\)

\(\Rightarrow\) \(BC=24cm-7cm-10cm=7cm\) 

\(\Rightarrow\) \(NP=7cm\)

Vậy \(AB=MN=7cm\), \(BC=NP=7cm\), \(AC=MP=10cm\).

2. Kí hiệu

Để kí hiệu sự bằng nhau của tam giác \(ABC\) và tam giác \(A'B'C'\) ta viết \(\Delta ABC=\Delta A'B'C'\).

Quy ước: Khi kí hiệu sự bằng nhau của hai tam giác, các chữ cái chỉ tên các đỉnh tương ứng được viết theo cùng thứ tự.

 Nếu \(\left\{{}\begin{matrix}AB=A'B';AC=A'C';BC=B'C'\\\widehat{A}=\widehat{A'};\widehat{B}=\widehat{B'};\widehat{C}=\widehat{C'}\end{matrix}\right.\)  \(\Rightarrow\) \(\Delta ABC=\Delta A'B'C'\)

+) \(\Delta ABC=\Delta A'B'C'\) là cách viết đúng,

+) hay \(\Delta BAC=\Delta B'A'C'\) cũng là một cách viết đúng...

+) \(\Delta ABC=\Delta B'C'A'\) là cách viết sai;

+) hay \(\Delta CAB=\Delta B'C'A'\) cũng là một cách viết sai...

Tương tự: \(\Delta DEF=\Delta MNP\) nếu \(\left\{{}\begin{matrix}DE=MN;EF=NP;DF=MP\\\widehat{D}=\widehat{M};\widehat{E}=\widehat{N};\widehat{F}=\widehat{P}\end{matrix}\right.\)

Ví dụ: Cho \(\Delta IHK=\Delta DEF\), biết \(\widehat{I}=40^0\), \(\widehat{E}=60^0\). Tính \(\widehat{D}\), \(\widehat{K}\)?

Bài giải:

Vì \(\Delta IHK=\Delta DEF\) nên \(\widehat{I}=\widehat{D}=40^0\), \(\widehat{H}=\widehat{E}=60^0\), \(\widehat{K}=\widehat{F}\).

Xét trong \(\Delta IHK\) có \(\widehat{I}+\widehat{H}+\widehat{K}=180^0\)

 \(\Rightarrow\) \(\widehat{K}=180^0-\widehat{I}-\widehat{H}\)

\(\Rightarrow\) \(\widehat{K}=180^0-40^0-60^0=80^0\)

Vậy \(\widehat{D}=40^0\), \(\widehat{K}=80^0\).