 chi tiết nhất ạ
chi tiết nhất ạ
HT
Những câu hỏi liên quan
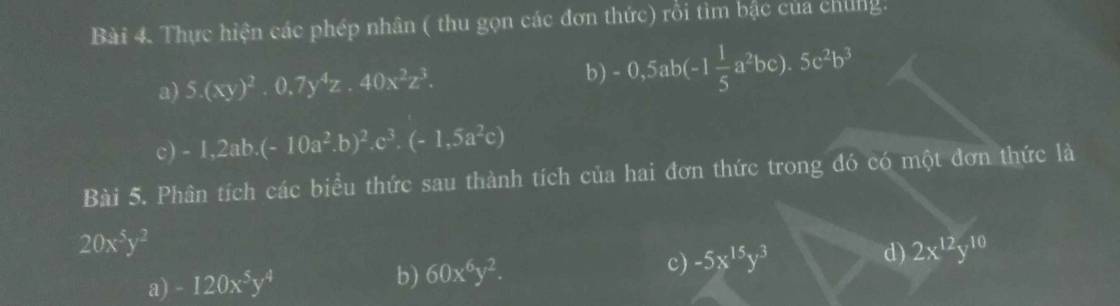 làm chi tiết ạ mik mới học nên cầm chi tiết nhất
làm chi tiết ạ mik mới học nên cầm chi tiết nhất
5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)
Đúng 0
Bình luận (0)
Chi tiết em nới học nên làm chi tiết nhất ạ  đề bài rút gọn phân thức
đề bài rút gọn phân thức
\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
Đúng 3
Bình luận (0)
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)
Đúng 1
Bình luận (0)
Chi tiết nhất ạ thanks mn nhiều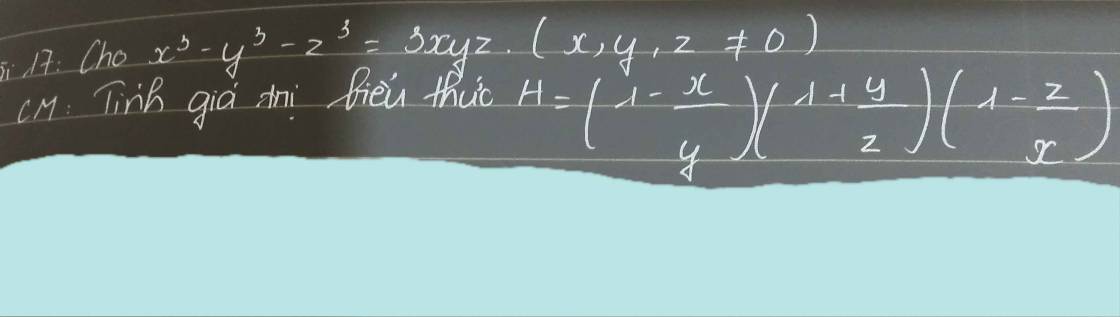
\(x^3-y^3-z^3=3xyz\)
=>\(\left(x-y\right)^3-z^3+3xy\left(x-y\right)-3xyz=0\)
=>\(\left(x-y-z\right)\left[\left(x-y\right)^2+z\left(x-y\right)+z^2\right]+3xy\left(x-y-z\right)=0\)
=>\(\left(x-y-z\right)\left[x^2-2xy+y^2+xz-zy+z^2+3xy\right]=0\)
=>\(\left(x-y-z\right)\left(x^2+y^2+z^2+xy+xz-yz\right)=0\)
=>\(\left(x-y-z\right)\left(2x^2+2y^2+2z^2+2xy+2xz-2yz\right)=0\)
=>\(\left(x-y-z\right)\left[\left(x^2+2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(x^2+2xz+z^2\right)\right]=0\)
=>\(\left(x-y-z\right)\left[\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2\right]=0\)
=>\(\left[{}\begin{matrix}x-y-z=0\\\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=y+z\\y=z=-x\end{matrix}\right.\)
\(H=\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1-\dfrac{z}{x}\right)\)
\(=\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}\cdot\dfrac{x-z}{x}\)
TH1: x=y+z
=>\(H=\dfrac{y-x}{y}\cdot\dfrac{x}{z}\cdot\dfrac{x-z}{x}\)
\(=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{y-x}{y}=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{-z}{y}=-1\)
TH2: y=z=-x
=>y+x+z=0(vô lý vì x,y,z đều dương)
Vậy: H=-1
Đúng 1
Bình luận (0)
Chi tiết nhất ạ e cảm ơn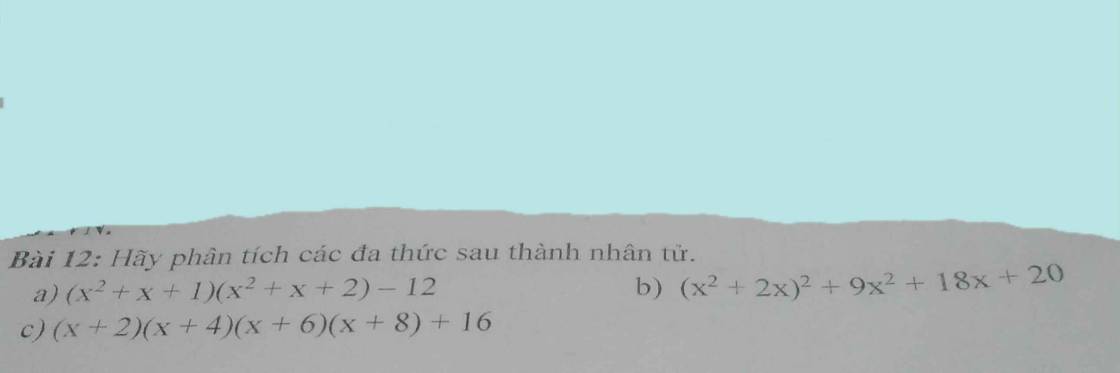
a) \(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt: \(x^2+x+1=y\), khi đó biểu thức trở thành:
\(y\left(y+1\right)-12\)
\(=y^2+y-12\)
\(=y^2-3y+4y-12\)
\(=y\left(y-3\right)+4\left(y-3\right)\)
\(=\left(y-3\right)\left(y+4\right)\)
\(=\left(x^2+x+1-3\right)\left(x^2+x+1+4\right)\)
\(=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
\(=\left(x^2-x+2x-2\right)\left(x^2+x+5\right)\)
\(=\left[x\left(x-1\right)+2\left(x-1\right)\right]\left(x^2+x+5\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+5\right)\)
b) \(\left(x^2+2x\right)^2+9x^2+18x+20\)
\(=\left(x^2+2x\right)^2+9\left(x^2+2x\right)+20\)
Đặt: \(x^2+2x=a\), khi đó biểu thức trở thành:
\(a^2+9a+20\)
\(=a^2+4a+5a+20\)
\(=a\left(a+4\right)+5\left(a+4\right)\)
\(=\left(a+4\right)\left(a+5\right)\)
\(=\left(x^2+2x+4\right)\left(x^2+2x+5\right)\)
c) \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)
\(=\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]+16\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)
Đặt: \(x^2+10x+20=y\), khi đó biểu thức trở thành:
\(\left(y-4\right)\left(y+4\right)+16\)
\(=y^2-16+16\)
\(=y^2\)
\(=\left(x^2+10x+20\right)^2\)
$\text{#}Toru$
Đúng 3
Bình luận (0)
 chi tiết nhất trinhtrình bày từng bước 1 ạ
chi tiết nhất trinhtrình bày từng bước 1 ạ
a: Xét ΔKAB và ΔKCD có
\(\widehat{KAB}=\widehat{KCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AKB}=\widehat{CKD}\)(hai góc đối đỉnh)
Do đó: ΔKAB đồng dạng với ΔKCD
=>\(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(KA\cdot KD=KB\cdot KC\)
b: Ta có: \(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(\dfrac{KC}{KA}=\dfrac{KD}{KB}\)
=>\(\dfrac{KC}{KA}+1=\dfrac{KD}{KB}+1\)
=>\(\dfrac{KC+KA}{KA}=\dfrac{KD+KB}{KB}\)
=>\(\dfrac{AC}{KA}=\dfrac{BD}{KB}\)
=>\(\dfrac{AK}{AC}=\dfrac{BK}{BD}\left(1\right)\)
Xét ΔADC có IK//DC
nên \(\dfrac{AK}{AC}=\dfrac{IK}{DC}\left(2\right)\)
Xét ΔBDC có KQ//DC
nên \(\dfrac{KQ}{DC}=\dfrac{BK}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra IK=KQ
Đúng 1
Bình luận (0)
Trong tác phảm "Lão Hạc" đâu là chi tiết nghệ thuật quan trong nhất
A. Chi tiết lão Hạc tự tử bằng bả chó
B. Tất cả đáp án trên đều đúng
C. Chi tiết lão Hạc bán chó
D. Chi tiết lão Hạc xin bã chó Các bạn giúp mình với ạ
đáp án là B nhé bạn mik chắc luôn nhoa !
Tìm n ∈ N để n5 + 1 chia hết cho n3 + 1 Mong đc câu trả lời chính xác và nhanh nhất ạ, giải chi tiết dùm mình nha Mình đang cần gấp, mình cảm ơn ạ, giải chi tiết dùm mình nha
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
Đúng 0
Bình luận (0)

mọi người giải một cách chi tiết nhất cho e dc k ạ
d: ĐKXĐ: \(3x< >k\Omega\)
=>\(x< >\dfrac{k\Omega}{3}\)
\(cot^23x-cot3x-2=0\)
=>\(cot^23x-2cot3x+cot3x-2=0\)
=>\(\left(cot3x-2\right)\left(cot3x+1\right)=0\)
=>\(\left[{}\begin{matrix}cot3x-2=0\\cot3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}cot3x=2\\cot3x=-1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3x=arccot\left(2\right)+k\Omega\\3x=-\dfrac{\Omega}{4}+k\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{1}{3}\cdot arccot\left(2\right)+\dfrac{k\Omega}{3}\\x=-\dfrac{\Omega}{12}+\dfrac{k\Omega}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
có CTV nào đang on ko ạ? Trả lời chi tiết cho em câu hỏi mới nhất của em với ạ
Xem thêm câu trả lời





