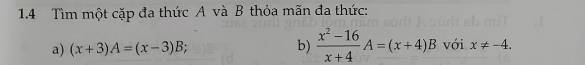
Bài 1: Phân thức đại số.
a.
\(\left(x+3\right)A=\left(x-3\right)B\Rightarrow\dfrac{A}{B}=\dfrac{x-3}{x+3}\)
\(\Rightarrow\left\{{}\begin{matrix}A=x-3\\B=x+3\end{matrix}\right.\)
b.
\(\dfrac{x^2-16}{x+4}A=\left(x+4\right)B\Rightarrow\dfrac{\left(x-4\right)\left(x+4\right)}{x+4}A=\left(x+4\right)B\)
\(\Rightarrow\left(x-4\right)A=\left(x+4\right)B\)
\(\Rightarrow\dfrac{B}{A}=\dfrac{x-4}{x+4}\)
\(\Rightarrow\left\{{}\begin{matrix}A=x+4\\B=x-4\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Chi tiết em nới học nên làm chi tiết nhất ạ  đề bài rút gọn phân thức
đề bài rút gọn phân thức
\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
Đúng 3
Bình luận (0)
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)
Đúng 1
Bình luận (0)
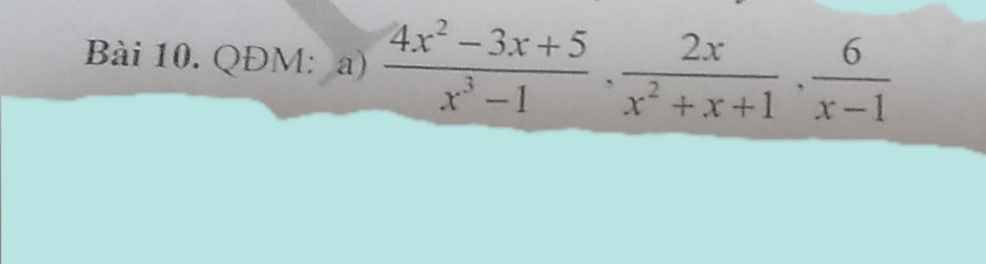 chi tietiêttiết
chi tietiêttiết
\(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
\(\Rightarrow MTC\) là \(\left(x-1\right)\left(x^2+x+1\right)\)
\(\dfrac{2x}{x^2+x+1}=\dfrac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\dfrac{6}{x-1}=\dfrac{6\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
Đúng 2
Bình luận (0)
 Làm luôn cho mình c40,41 nhé
Làm luôn cho mình c40,41 nhé
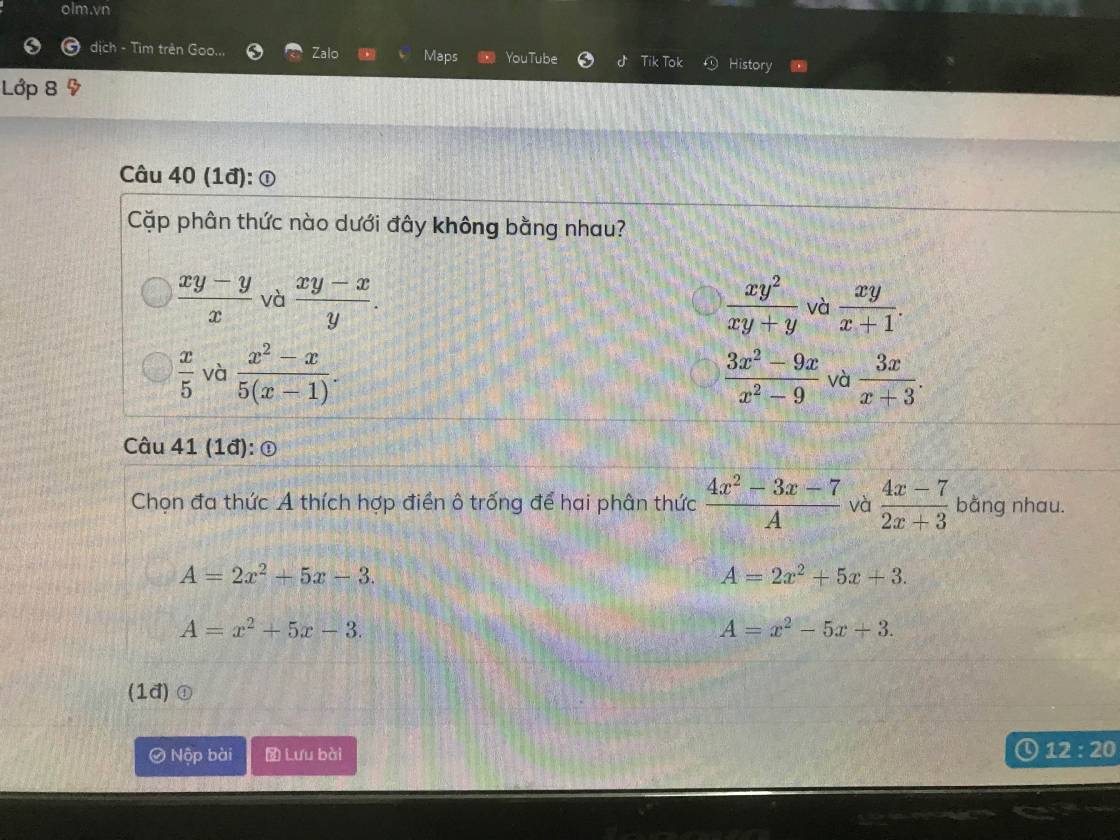
Câu 40: Đáp án thứ nhất
Câu 41: Đáp án thứ hai
Đúng 0
Bình luận (0)
Viết điều kiện xác định của phân thức dfrac{x+1}{x-1} và tính giá trị của phân thức tại x2GIÚP MÌNH VỚI MAI CÔ KỈM TRA RÙI
Đọc tiếp
Viết điều kiện xác định của phân thức \(\dfrac{x+1}{x-1}\) và tính giá trị của phân thức tại x=2
GIÚP MÌNH VỚI MAI CÔ KỈM TRA RÙI ![]()
![]()
![]()
\(\dfrac{2x+1}{x+1}-\dfrac{3x^2}{x-1}-\dfrac{x-2}{x+1}+\dfrac{3}{x-1}\)
Gấp giúp mình ạ
\(=\left(\dfrac{2x+1}{x+1}-\dfrac{x-2}{x+1}\right)-\left(\dfrac{3x^2}{x-1}-\dfrac{3}{x-1}\right)\)
\(=\left(\dfrac{2x+1-x+2}{x+1}\right)-\left(\dfrac{3x^2-3}{x-1}\right)\)
\(=\dfrac{x+3}{x-1}-\left[\dfrac{3\left(x^2-1\right)}{x-1}\right]\)
=\(\dfrac{x+3}{x-1}-\left[\dfrac{3\left(x-1\right)\left(x+1\right)}{x-1}\right]\)
\(\dfrac{x+3}{x-1}-3\left(x+1\right)\)
Đúng 1
Bình luận (0)
Rút gọn m(a+4)/a(m-3 )
p= x^2+2/x^3-1 + 2/x^2+x+1 - 1/x-1
a) Tìm điều kiện xác định và rút gọn
b) Tính giá trị của P biết x^2 - x =0
c) C/m rằng P luôn dương
Giúp với mình đang gấp
Lời giải:
a. ĐKXĐ: $x\neq 1$
\(P=\frac{x^2+2}{(x-1)(x^2+x+1)}+\frac{2(x-1)}{(x-1)(x^2+x+1)}-\frac{x^2+x+1}{(x-1)(x^2+x+1)}\)
\(=\frac{x^2+2+2x-2-x^2-x-1}{(x-1)(x^2+x+1)}=\frac{x-1}{(x-1)(x^2+x+1)}=\frac{1}{x^2+x+1}\)
b.
$x^2-x=0\Leftrightarrow x(x-1)=0$
$\Leftrightarrow x=0$ hoặc $x=1$
Vì $x\neq 1$ theo ĐKXĐ nên $x=0$
Khi đó: $P=\frac{1}{0^2+0+1}=1$
c.
Ta thấy:
$1>0$
$x^2+x+1=(x+\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $x\neq 1$
$\Rightarrow P=\frac{1}{x^2+x+1}>0$
Hay $P$ luôn dương với mọi $x\neq 1$
Đúng 3
Bình luận (0)
Cho D=\(\dfrac{2x+4}{3x-1}\) (x ≠ \(\dfrac{1}{3}\)).Tìm x nguyên để D có giá trị nguyên.
mn giúp mik vs ạ!!!
Để D là số nguyên thì \(2x+4⋮3x-1\)
=>\(6x+12⋮3x-1\)
=>\(6x-2+14⋮3x-1\)
=>\(14⋮3x-1\)
=>\(3x-1\in\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
=>\(3x\in\left\{2;0;3;-1;8;-6;15;-13\right\}\)
=>\(x\in\left\{\dfrac{2}{3};0;1;-\dfrac{1}{3};\dfrac{8}{3};-2;5;-\dfrac{13}{3}\right\}\)
mà x nguyên
nên \(x\in\left\{0;1;-2;5\right\}\)
Đúng 2
Bình luận (0)
Đọc tiếp
Yêu cầu và điều kiện đề là gì bạn nên ghi chú rõ để mọi người hỗ trợ bạn được tốt hơn nhé.
Đúng 0
Bình luận (0)





