Tìm nguyên hàm của I = ∫ 2 x x 2 − 1 d x bằng cách đặt u = x 2 − 1 , mệnh đề nào dưới đây đúng?
A. I = 2 ∫ u d u
B. I = ∫ 2 u d u
C. I = ∫ u d u
D. I = 1 2 ∫ u d u
Giải phương trình bằng cách đặ ẩn phụ:
\(3\left(x^2+x\right)^2-2\left(x^2+x\right)-1=0\)
Cho hàm số y = ( x - 2 ) - 1 2 Bạn Toán tìm tập xác định của hàm số bằng cách như sau:
Bước 1: Ta có y = 1 ( x - 2 ) 1 2 = 1 x - 2
Bước 2: Hàm số xác định ⇔ x - 2 > 0 ⇔ x > 2
Bước 3: Vậy tập xác định của hàm số là D = ( 2 ; + ∞ )
Lời giải trên của bạn toán đúng hay sai? Nếu sai thì sai ở bước nào?
A. Bước 3
B. Bước 1
C. Đúng
D. Bước 2
tìm nguyên hàm của (x+1)sin2x
tìm nguyên hàm của (x.sin(x/2)).(x.cos(x/2))
tìm nguyên hàm của 1/(x.lnx.ln(lnx))
c1; sin2x=1-cos2x/2 roi tung phan
c2 ;nhan vo duocx2(sinx/2 .cosx/2)=x2/2(sinx+cosx) lai nhan vo roi tung phan nhe
Cho hàm số y = (-1)/2 x2.
Trên đồ thị của hàm số này, xác định điểm D có hoành độ bằng 3. Tìm tung độ của điểm D bằng hai cách: bằng đồ thị; bằng cách tính y với x = 3. So sánh hai kết quả.
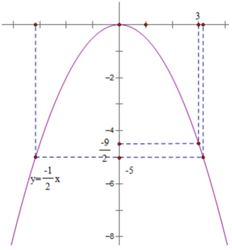
Từ đồ thị, ta xác định được tung độ của điểm D là (-9)/2
Với x = 3 ta có: y = (-1)/2 x2 = (-1)/2.32 = (-9)/2
Hai kết quả là như nhau.
EM CẦN GẤP Ạ..GIÚP EM VỚI Ạ..
1)Cho hàm số y=(m-1)x+m (d)
a)Tìm m để (d) là đồ thị của hàm số bậc nhất
b)Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng 1
c)Chứng minh (d) luôn đi qua 1 điểm cố định với mọi m
2)Cho 3 đường thẳng d1:y=x-2;d2:y=2-x;d3:y=(2-m)x+1
a)Tìm m để d1;d2;d3 đồng quy
b)Tính khoảng cách từ gốc tọa độ đến đường thẳng d2
c)Tính góc tạo bởi đường thẳng d1 và trục Ox
Bài 2:
a: Phương trình hoành độ giao điểm là:
x-2=2-x
\(\Leftrightarrow2x=4\)
hay x=2
Thay x=2 vào (d1), ta được:
y=2-2=0
Thay x=2 và y=0 vào (d3), ta được:
2(2-m)+1=0
\(\Leftrightarrow4-2m+1=0\)
hay \(m=\dfrac{5}{2}\)
1/ Tìm nguyên hàm:
\(\int\dfrac{dx}{x^2.\sqrt{x^2+1}}\)
2, Đường thẳng d: \(\dfrac{x+1}{2}=\dfrac{y-1}{-1}=\dfrac{z-2}{-1}\). Gọi (P) là mặt phẳng chưa đường thẳng d và tạo với mp (Oxy) một góc nhỏ nhất. Tính khoảng cách từ M (0,3,-4) đến mp (P).
\(I=\int\dfrac{\sqrt{x^2+1}}{x^2\left(x^2+1\right)}dx=\int\left(\dfrac{\sqrt{x^2+1}}{x^2}-\dfrac{1}{\sqrt{x^2+1}}\right)dx\)
\(=\int\dfrac{\sqrt{x^2+1}}{x^2}dx-\int\dfrac{1}{\sqrt{x^2+1}}dx=I_1-I_2\)
Xét \(I_1=\int\dfrac{\sqrt{x^2+1}}{x^2}dx\)
Đặt \(\left\{{}\begin{matrix}u=\sqrt{x^2+1}\\dv=\dfrac{1}{x^2}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{x}{\sqrt{x^2+1}}dx\\v=-\dfrac{1}{x}\end{matrix}\right.\)
\(\Rightarrow I_1=-\dfrac{\sqrt{x^2+1}}{x}+\int\dfrac{1}{\sqrt{x^2+1}}dx=-\dfrac{\sqrt{x^2+1}}{x}+I_2\)
\(\Rightarrow I=-\dfrac{\sqrt{x^2+1}}{x}+I_2-I_2=-\dfrac{\sqrt{x^2+1}}{x}+C\)
2.
Gọi d' là hình chiếu của d lên Oxy, M là giao điểm của d và Oxy
Khi đó với mọi đường thẳng d'' nào đó đi qua M thì đều tạo với d 1 góc lớn hơn góc giữa d và d'
Hay góc giữa (P) và Oxy nhỏ nhất là góc giữa d và d'
Điều này xảy ra khi d và d' vuông góc \(d_1\) , trong đó \(d_1\) là giao tuyến của (P) và Oxy
Tới đây thì chắc đơn giản:
- Tìm vtcp \(\overrightarrow{u_{d_1}}\) với \(d_1\) thuộc Oxy, qua M và vuông góc d
- (P) sẽ nhận \(\left[\overrightarrow{u_d};\overrightarrow{u_{d1}}\right]\) là 1 vtpt và đi qua M
Tìm nguyên hàm của hàm số : \(\int\dfrac{x\ln\left(x+\sqrt{x^2+1}\right)}{\sqrt{x^2+1}}dx\)
Lời giải:
Đặt \(u=\ln (x+\sqrt{x^2+1}); dv=\frac{1}{\sqrt{x^2+1}}dx\)
\(\Rightarrow du=\frac{dx}{\sqrt{x^2+1}}; v=\int \frac{x}{\sqrt{x^2+1}}dx=\frac{1}{2}\int \frac{d(x^2+1)}{\sqrt{x^2+1}}=\sqrt{x^2+1}\)
\(\Rightarrow \int \frac{x\ln (x+\sqrt{x^2+1})}{\sqrt{x^2+1}}dx=\int udv=uv-vdu=\sqrt{x^2+1}\ln (x+\sqrt{x^2+1})-\int dx\)
\(=\sqrt{x^2+1}\ln (x+\sqrt{x^2+1})-x+C\)
Bài 1: Cho hàm số y=f(x)=ax4-bx2+x+3. Biết f(2)=17. Tính f(-2)
Bài 2: Cho(d):y=-x+2
a) Vẽ (d)
b) Tìm các điểm nằm trên (d) sao cho khoảng cách từ điểm đó đến trục Ox bằng 2 làn khoảng cách từ đó đến trục Oy
Cho hàm số :
\(y=x+m+\frac{m}{x-2}\)
Tìm m để hàm số có cực đại và cực tiểu sao cho 2 điểm cực trị của đồ thị hàm số cách đường thẳng d : x-y+2 =0 những khoảng cách bằng nhau.
Với \(x\ne2\) ta có \(y=1-\frac{m}{\left(x-2\right)^2}\)
Hàm số có cực đại và cực tiểu \(\Leftrightarrow\) phương trình \(\left(x-2\right)^2-m=0\) (1) có 2 nghiệm phân biệt khác 2 \(\Leftrightarrow m>0\)
Với m>0 phương trình (1) có 2 nghiệm là :
\(x_1=2+\sqrt{m}\Rightarrow y_1=2+m+2\sqrt{m}\)
\(x_2=2-\sqrt{m}\Rightarrow y_2=2+m-2\sqrt{m}\)
Hai điểm cực trị của đồ thị hàm số \(A\left(2-\sqrt{m};2+m-2\sqrt{m}\right);B\left(\left(2+\sqrt{m};2+m+2\sqrt{m}\right)\right)\)
Khoảng cách từ A và B tới d bằng nhau nên ta có phương trình :
\(\left|2-m-\sqrt{m}\right|=\left|2-m+\sqrt{m}\right|\)
\(\Leftrightarrow\begin{cases}m=0\\m=2\end{cases}\)
Đối chiếu điều kiện thì m=2 thỏa mãn bài toán. Vậy yêu cầu bài toán là m=2
Tìm nguyên hàm của hàm số f(x) = (x – 1)2.
A. ∫ f x d x = x - 1 2 2 + C
B. ∫ f x d x = 2 x - 1 + C
C. ∫ f x d x = x - 1 3 2 + C
D. ∫ f x d x = x 3 3 + C