Chương 3: NGUYÊN HÀM. TÍCH PHÂN VÀ ỨNG DỤNG
NP
17 tháng 11 2023 lúc 22:25
Cho biết \(30x^{\dfrac{1}{3}}y^{\dfrac{2}{3}}=360\). Tìm \(\dfrac{dy}{dx}\left(27,8\right)\)
Version:0.9 StartHTML:0000000105 EndHTML:0000016865 StartFragment:0000000141 EndFragment:0000016825 Câu 13. Tính các giới hạn sau: (a) limx→3 √ 1 + x − 2 x − 3 . (b) limx→0 x √x + 1 − 1. (c) limx→0 √ 1 + 4x − 1 1 − 3√1 − 6x. Câu 14. Tính các giới hạn sau: (a) limx→0 ln(cos x) ln(1 + ax2). (b) limx→0 ln(1 + 3x) tan x . (c) limx→0 √ 1 + 3x − 1 sin x . Câu 15. Tính các giới hạn sau: (a) limx→0 ex − e−x ln(1 + x). (b) limx→1 x − 1 + ln x ex − e . (c) limx→0 ex − x − 1 ex − 1 . (d) limx→1 x3 − 1 1 −...
Đọc tiếp
Version:0.9 StartHTML:0000000105 EndHTML:0000016865 StartFragment:0000000141 EndFragment:0000016825
Câu 13. Tính các giới hạn sau: (a) limx→3 √ 1 + x − 2 x − 3 . (b) limx→0 x √x + 1 − 1. (c) limx→0 √ 1 + 4x − 1 1 − 3√1 − 6x. Câu 14. Tính các giới hạn sau: (a) limx→0 ln(cos x) ln(1 + ax2). (b) limx→0 ln(1 + 3x) tan x . (c) limx→0 √ 1 + 3x − 1 sin x . Câu 15. Tính các giới hạn sau: (a) limx→0 ex − e−x ln(1 + x). (b) limx→1 x − 1 + ln x ex − e . (c) limx→0 ex − x − 1 ex − 1 . (d) limx→1 x3 − 1 1 − x
NH
30 tháng 11 2022 lúc 21:24
Cho hàm số f(x) liên tục trên [0;1] thoả mãn \(\int_0^1f\left(x\right)dx=2\) và \(\int_0^1xf\left(x\right)dx=\dfrac{3}{2}\). Tìm giá trị nhỏ nhất của \(\int_0^1\left[f\left(x\right)\right]^2dx\)
Giúp em câu này với ạ ! Toán cao cấp 1 em cảm ơn
NH
13 tháng 5 2022 lúc 0:49
Cho hàm số y=f(x) liên tục trên [0;+\(\infty\)] và \(\int_0^{x^2}f\left(t\right)dt=x.sin\pi x\). Tính f(4)
đặt :
\(F\left(x\right)=\int_0^{x^2}f\left(t\right)dt=xsin\left(\pi x\right)\Leftrightarrow F\left(x^2\right)-F\left(0\right)=xsin\)
\(\left(\pi x\right)\Leftrightarrow F\left(x^2\right)=F\left(0\right)+xsin\left(\pi x\right)\)
lấy đạo hàm \(2\) vế , ta có :
\(\left(F\left(0\right)\right)'=sin\left(\pi x\right)+\pi xcos\left(\pi x\right)+\left(F\left(0\right)\right)'\)
\(\Leftrightarrow2xf\left(x^2\right)=sin\left(\pi x\right)+\pi xcos\left(\pi x\right)\)
thay \(x=2\) , ta có :
\(2.2.f\left(4\right)=sin\left(2\pi\right)+2\pi cos\left(2\pi\right)\Leftrightarrow4f\left(4\right)=2\pi\Leftrightarrow f\left(4\right)=\dfrac{\pi}{2}\)
Đúng 1
Bình luận (0)
Tính tích phân: \(\int\limits^{log\left(1+\sqrt{2}\right)}_0\left(\dfrac{e^x-e^{-x}}{2}\right)^3\cdot\left(\dfrac{e^x+e^{-x}}{2}\right)^{11}dx\)
Cho hàm số \(f\left(x\right)\) có đạo hàm \(f'\left(x\right)\) trên đoạn \(\left[0;1\right]\) thoả mãn \(f\left(1\right)=4\) và \(\int\limits^1_0f\left(x\right)dx=3\). Tính tích phân \(\int\limits^1_0x^3f'\left(x^2\right)dx\)
H24
5 tháng 5 2022 lúc 23:26
Cho hai hàm đa thức fleft(xright)ax^3+bx^2+cx+d và gleft(xright)mx^2+nx+p. Biết rằng đồ thị hai hàm số yfleft(xright) và ygleft(xright) cắt nhau tại ba điểm có hoành độ -1;2;4, đồng thời cắt trục tung tại M,N sao cho MN6 (tham khảo hình vẽ). Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho (phần gạch sọc) có diện tích bằngA. dfrac{125}{8} B. dfrac{253}{24} C. dfrac{253}{16} D. dfrac{253}{12}Giải thích phần bôi vàng cho mình với ạ, mình cảm ơn nhiều♥
Đọc tiếp
Cho hai hàm đa thức \(f\left(x\right)=ax^3+bx^2+cx+d\) và \(g\left(x\right)=mx^2+nx+p\). Biết rằng đồ thị hai hàm số \(y=f\left(x\right)\) và \(y=g\left(x\right)\) cắt nhau tại ba điểm có hoành độ \(-1;2;4\), đồng thời cắt trục tung tại \(M,N\) sao cho \(MN=6\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho (phần gạch sọc) có diện tích bằng
A. \(\dfrac{125}{8}\) B. \(\dfrac{253}{24}\) C. \(\dfrac{253}{16}\) D. \(\dfrac{253}{12}\)
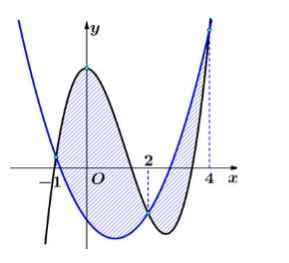
Giải thích phần bôi vàng cho mình với ạ, mình cảm ơn nhiều♥
vì -1, 2, 4 là giao điểm của 2 đồ thị nên là nghiệm của pt f(x) - g(x)
f(x) và g(x) bậc cao nhất là bậc 3 nên viết được như trên
Đúng 1
Bình luận (1)
H24
24 tháng 4 2022 lúc 15:03
Tính tích phân \(I=\int\limits^{\dfrac{\Pi}{2}}_0\left(2cos^2\dfrac{x}{2}+xcosx\right)e^{sinx}dx\)
Giúp mình với ạ♥
\(I=\int\limits^{\dfrac{\pi}{2}}_0\left(1+cosx+x.cosx\right)e^{sinx}dx=\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx+\int\limits^{\dfrac{\pi}{2}}_0\left(x+1\right).cosx.e^{sinx}dx=I_1+I_2\)
Xét \(I_2\), đặt \(\left\{{}\begin{matrix}u=x+1\\dv=cosx.e^{sinx}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^{sinx}\end{matrix}\right.\)
\(\Rightarrow I_2=\left(x+1\right).e^{sinx}|^{\dfrac{\pi}{2}}_0-\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx=\left(\dfrac{\pi}{2}+1\right)e-1-I_1\)
\(\Rightarrow I=I_1+\left(\dfrac{\pi}{2}+1\right)e-1-I_1=\left(\dfrac{\pi}{2}+1\right)e-1\)
Đúng 1
Bình luận (6)