Bài 3: Đồ thị của hàm số y = ax + b ( a khác 0)

Thay x=1 và y=2 vào y=ax-2a-1, ta được:

\(a\cdot1-2a-1=2\)

=>-a=3

=>a=-3

ai giải hộ mik ko

Câu 2:

a: 

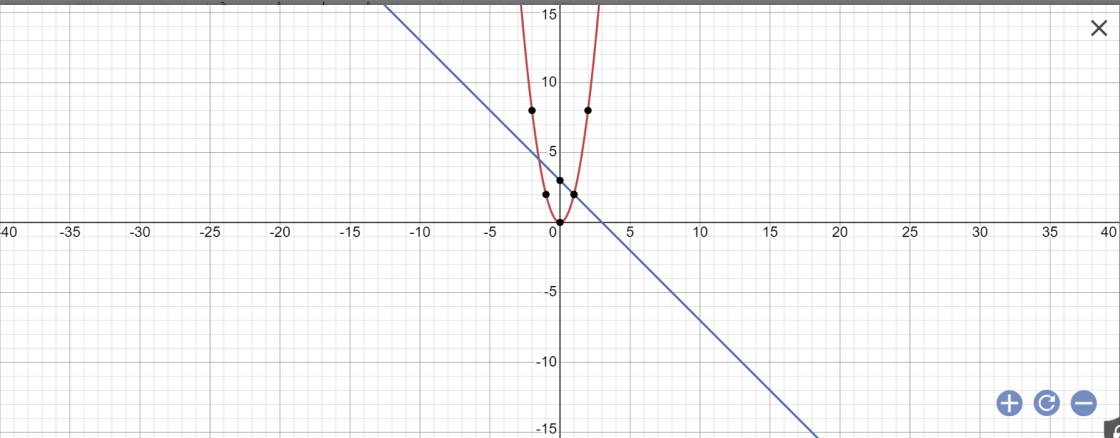
b: phương trình hoành độ giao điểm là:

\(2x^2=-x+3\)

=>\(2x^2+x-3=0\)

=>\(2x^2+3x-2x-3=0\)

=>(2x+3)(x-1)=0

=>\(\left[{}\begin{matrix}2x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=1\end{matrix}\right.\)

Thay x=-3/2 vào (P), ta được:

\(y=2\cdot\left(-\dfrac{3}{2}\right)^2=2\cdot\dfrac{9}{4}=\dfrac{9}{2}\)

Thay x=1 vào (P), ta được:

\(y=2\cdot1^2=2\)

Vậy: (P) cắt (d) tại hai điểm là \(A\left(-\dfrac{3}{2};\dfrac{9}{2}\right);B\left(1;2\right)\)

y=(m-1)x+2

=>(m-1)x-y+2=0

Khoảng cách từ O đến (d) là:

\(\dfrac{\left|0\left(m-1\right)+0\left(-1\right)+2\right|}{\sqrt{\left(m-1\right)^2+1}}=\dfrac{2}{\sqrt{\left(m-1\right)^2+1}}\)

Để khoảng cách từ O đến (d) bằng \(\sqrt{2}\) thì \(\dfrac{2}{\sqrt{\left(m-1\right)^2+1}}=\sqrt{2}\)

=>\(\sqrt{\left(m-1\right)^2+1}=\sqrt{2}\)

=>\(\left(m-1\right)^2+1=2\)

=>\(\left(m-1\right)^2=1\)

=>\(\left[{}\begin{matrix}m-1=1\\m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=0\end{matrix}\right.\)

a.

Do ĐTHS song song với \(y=-x-2\Rightarrow a=-1\)

Do đồ thị qua A nên:

\(a.1+b=2\Rightarrow b=2-a=3\)

Vậy pt hàm số có dạng: \(y=-x+3\)

b.

Do đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2 nên:

\(-2=a.0+b\Rightarrow b=-2\)

Do ĐTHS cắt trục hoành tại điểm có hoành độ -2

\(\Rightarrow0=a.\left(-2\right)+b\Rightarrow a=\dfrac{b}{2}=-1\)

Vậy hàm số có dạng: \(y=-x-2\)

b: Thay x=1 và y=4 vào (d), ta được:

\(1\left(m+1\right)+2=4\)

=>m+3=4

=>m=4-3=1

c: Thay x=1 và y=0 vào (d), ta được:

\(1\left(m+1\right)+2=0\)

=>m+3=0

=>m=-3

Thay x=2 và y=1 vào (d), ta được:

\(2\left(m^2-2m+3\right)+4=1\)

=>\(2m^2-4m+6+4-1=0\)

=>\(2m^2-4m+9=0\)

=>\(m^2-2m+\dfrac{9}{2}=0\)

=>\(m^2-2m+1+\dfrac{7}{2}=0\)

=>\(\left(m-1\right)^2+\dfrac{7}{2}=0\)(vô lý)

Vậy: \(m\in\varnothing\)

Bài 4:

Thay x=0 và y=-2 vào y=ax+b, ta được:

\(a\cdot0+b=-2\)

=>b+0=-2

=>b=-2

Vậy: y=ax-2

Thay x=3 và y=0 vào y=ax-2, ta được:

\(3\cdot a-2=0\)

=>3a=2

=>\(a=\dfrac{2}{3}\)

Vậy: \(y=\dfrac{2}{3}x-2\)

Câu 2:

a: Tung độ góc của hàm số là 5 nên (d): y=ax+b đi qua A(0;5)

Thay x=0 và y=5 vào (d), ta được:

\(a\cdot0+b=5\)

=>b+0=5

=>b=5

=>(d): y=ax+5

Vì (d)//y=3x nên a=3

=>(d): y=3x+5

b: Vì (d)//y=-2x nên \(\left\{{}\begin{matrix}a=-2\\b< >0\end{matrix}\right.\)

vậy: (d): y=-2x+b
Thay x=0 và y=8 vào (d), ta được:

\(-2\cdot0+b=8\)

=>b=8

Vậy: (d): y=-2x+8

c: Thay x=0 và y=2 vào (d), ta được:

\(a\cdot0+b=2\)

=>b+0=2

=>b=2

Vậy: (d): y=ax+2

Thay x=1 và y=4 vào (d), ta được:

\(a\cdot1+2=4\)

=>a+2=4

=>a=2

Vậy: (d): y=2x+2

mọi ng giúp mik câu 2,3,4 với ạ

b: y=-3x-x+3=-4x+3

Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\-3x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\3x=2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\x=\dfrac{2}{3}\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\-4x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-4x=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{3}{4}\\y=0\end{matrix}\right.\)

Tọa độ C là:

\(\left\{{}\begin{matrix}-3x+2=-4x+3\\y=-3x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x+4x=3-2\\y=-3x+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=1\\y=-3\cdot1+2=-3+2=-1\end{matrix}\right.\)

Vậy: \(A\left(\dfrac{2}{3};0\right);B\left(\dfrac{3}{4};0\right);C\left(1;-1\right)\)

c: \(AB=\sqrt{\left(\dfrac{3}{4}-\dfrac{2}{3}\right)^2+\left(0-0\right)^2}\)

\(=\sqrt{\left(\dfrac{9-8}{12}\right)^2}=\dfrac{1}{12}\)

\(AC=\sqrt{\left(1-\dfrac{2}{3}\right)^2+\left(-1-0\right)^2}=\sqrt{\left(\dfrac{1}{3}\right)^2+1^2}=\sqrt{1+\dfrac{1}{9}}=\sqrt{\dfrac{10}{9}}=\dfrac{\sqrt{10}}{3}\)

\(BC=\sqrt{\left(1-\dfrac{3}{4}\right)^2+\left(-1-0\right)^2}\)

\(=\sqrt{\left(\dfrac{1}{4}\right)^2+\left(-1\right)^2}\)

\(=\sqrt{\dfrac{1}{16}+1}=\sqrt{\dfrac{17}{16}}=\dfrac{\sqrt{17}}{4}\)

Thay x=0 và y=4 vào (d): y=ax+b, ta được:

\(a\cdot0+b=4\)

=>b=4

=>(d): y=ax+4

Thay x=2 và y=-1 vào (d), ta được:

2a+4=-1

=>2a=-5

=>\(a=-\dfrac{5}{2}\)