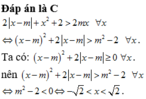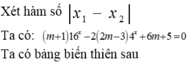Tìm tất cả các giá trị của m để bất phương trình \(2\left|x-m\right|+x^2+2>2mx\) thỏa mãn với mọi x
LT
Những câu hỏi liên quan
Tìm tất cả các giá trị của m để bất phương trình
2
|
x
-
m
|
+
x
2
+
2
2
m
x
thỏa mãn với mọi x A.
m
-
2
B. không tồn tại m C.
-
2
m
2
D.
m
2
Đọc tiếp
Tìm tất cả các giá trị của m để bất phương trình 2 | x - m | + x 2 + 2 > 2 m x thỏa mãn với mọi x
A. m > - 2
B. không tồn tại m
C. - 2 < m < 2
D. m < 2
Tìm tập hợp tất cả các giá trị của tham số m để bất phương trình
12
x
+
(
2
-
m
)
6
x
+
3
x
0
thỏa mãn với mọi x dương.
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số m để bất phương trình 12 x + ( 2 - m ) 6 x + 3 x > 0 thỏa mãn với mọi x dương.
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị của tham số m để phương trình \(x^2-2mx+m+2=0\) có 2 nghiệm \(x_1,x_2\) thỏa mãn \(x_1^3+x_2^3\le16\)
( Mong mọi người giúp đỡ )
\(\Delta'=m^2-\left(m+2\right)\ge0\Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-1\end{matrix}\right.\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m+2\end{matrix}\right.\)
\(x_1^3+x_2^3\le16\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\le16\)
\(\Leftrightarrow8m^3-6m\left(m+2\right)-16\le0\)
\(\Leftrightarrow4m^3-3m^2-6m-8\le0\)
\(\Leftrightarrow\left(m-2\right)\left(4m^2+5m+4\right)\le0\)
\(\Leftrightarrow\left(m-2\right)\left[\left(2m+\dfrac{5}{4}\right)^2+\dfrac{39}{16}\right]\le0\)
\(\Leftrightarrow m\le2\) (2)
Kết hợp (1); (2) \(\Rightarrow\left[{}\begin{matrix}m=2\\m\le-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị của m để phương trình \(x^2-\left(m-1\right)x+\left(m+3\right)=0\) có 2 nghiệm phân biệt x1, x2 thỏa mãn \(x_1^2+x_2^2\) đạt giá trị nhỏ nhất.
\(\Delta=\left(m-1\right)^2-4\left(m+3\right)=m^2-6m-11>0\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=m+3\end{matrix}\right.\)
Ta có:
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m-1\right)^2-2\left(m+3\right)=m^2-4m-5\)
Biểu thức này ko tồn tại cả min lẫn max với điều kiện m từ (1)
Đúng 1
Bình luận (0)
Cho phương trình \(x^2-\left(m+1\right)x+2-8=0\) (1), m là tham số.
a) giải phương trình (1) khi m=2.
b) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn
\(x^2_1+x_2^2+\left(x1-2\right)\left(x2-2\right)=11\)
a:Sửa đề: x^2-(m+1)x+2m-8=0
Khi m=2 thì (1) sẽ là x^2-3x-4=0
=>(x-4)(x+1)=0
=>x=4 hoặc x=-1
b: Δ=(-m-1)^2-4(2m-8)
=m^2+2m+1-8m+32
=m^2-6m+33
=(m-3)^2+24>=24>0
=>(1) luôn có hai nghiệm pb
\(x_1^2+x_2^2+\left(x_1-2\right)\left(x_2-2\right)=11\)
=>(x1+x2)^2-2x1x2+x1x2-2(x1+x2)+4=11
=>(m+1)^2-(2m-8)-2(m+1)+4=11
=>m^2+2m+1-2m+8-2m-2+4=11
=>m^2-2m=0
=>m=0 hoặc m=2
Đúng 1
Bình luận (0)
Bài 1. Tìm m để f (x)=mx^2 -2(m-1)x+4m-1 luôn dương Bài 2 tìm tất cả các giá trị của tham số m để bất phương trình sau có nghiệm đúng với mọi a.5x^2-x+m>0 b.m(m+2)x^2+2mx+2>0
Tìm tất cả các giá trị của tham số m để phương trình \(x^2-2mx+m+2=0\) có hai nghiệm phân biệt \(x_1,x_2\)thỏa mãn \(x^3_1+x_2^3\le16\)
Để pt có 2 nghiệm phân biệt thì \(\Delta'=m^2-\left(m+2\right)>0\Leftrightarrow\left(m+1\right)\left(m-2\right)>0\Leftrightarrow\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\). (1)
Khi đó theo hệ thức Viète ta có \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m+2\end{matrix}\right.\).
Ta có \(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\left(2m\right)^3-3.2m.\left(m+2\right)=8m^3-6m^2-12m\).
Do đó \(8m^3-6m^2-12m\le16\Leftrightarrow\left(m-2\right)\left(8m^2+10m+8\right)\le0\Leftrightarrow m\le2\)
(do \(8m^2+10m+8=2\left(2m+\dfrac{5}{4}\right)^2+\dfrac{39}{8}>0\forall m\)).
Kết hợp vs (1) ta có m < -1.
Đúng 2
Bình luận (0)
Bài 1: Tìm m để fleft(xright)mx^2-2left(m-1right)x+4m luôn luôn âm.Bài 2: Tìm tất cả các giá trị của tham số m để bất phương trình dfrac{-x^2+2x-5}{x^2-mx+1}le0nghiệm đúng với mọi xin RBài 3: Cho hàm số fleft(xright)-x^2-2left(m-1right)x+2m-1. Tìm tất cả các giá trị của tham số m để fleft(xright)0,forall xinleft(0;1right)
Đọc tiếp
Bài 1: Tìm m để \(f\left(x\right)=mx^2-2\left(m-1\right)x+4m\) luôn luôn âm.
Bài 2: Tìm tất cả các giá trị của tham số m để bất phương trình \(\dfrac{-x^2+2x-5}{x^2-mx+1}\le0\)nghiệm đúng với mọi \(x\in R\)
Bài 3: Cho hàm số \(f\left(x\right)=-x^2-2\left(m-1\right)x+2m-1\). Tìm tất cả các giá trị của tham số m để \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
1.
Nếu \(m=0\), \(f\left(x\right)=2x\)
\(\Rightarrow m=0\) không thỏa mãn
Nếu \(x\ne0\)
Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m< 0\\\Delta'=\left(m-1\right)^2-4m^2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m< -\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
2.
\(\dfrac{-x^2+2x-5}{x^2-mx+1}\le0\forall x\)
\(\Leftrightarrow\dfrac{-\left(x-1\right)^2-4}{x^2-mx+1}\le0\forall x\)
\(\Leftrightarrow x^2-mx+1>0\forall x\)
\(\Leftrightarrow\Delta=m^2-4< 0\Leftrightarrow-2< m< 2\)
Kết luận: \(-2< m< 2\)
Đúng 0
Bình luận (0)
giúp mình với ạ cảm ơn nhiều ^^
Tìm tất cả các giá trị m để phương trình \(x^2-\left(m-1\right)x+m+2=0\) có 2 nghiệm phân biệt thỏa mãn \(x_1< x_2< 1\)
\(\Delta=\left(m-1\right)^2-4\left(m+2\right)>0\)
\(\Leftrightarrow m^2-6m-7>0\Rightarrow\left[{}\begin{matrix}m>7\\m< -1\end{matrix}\right.\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=m+2\end{matrix}\right.\)
Để \(x_1< x_2< 1\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-1\right)\left(x_2-1\right)>0\\\dfrac{x_1+x_2}{2}< 1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-\left(x_1+x_2\right)+1>0\\\dfrac{m-1}{2}< 1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4>0\\m< 3\end{matrix}\right.\)
Kết hợp với (1) ta được: \(m< -1\)
Đúng 1
Bình luận (1)