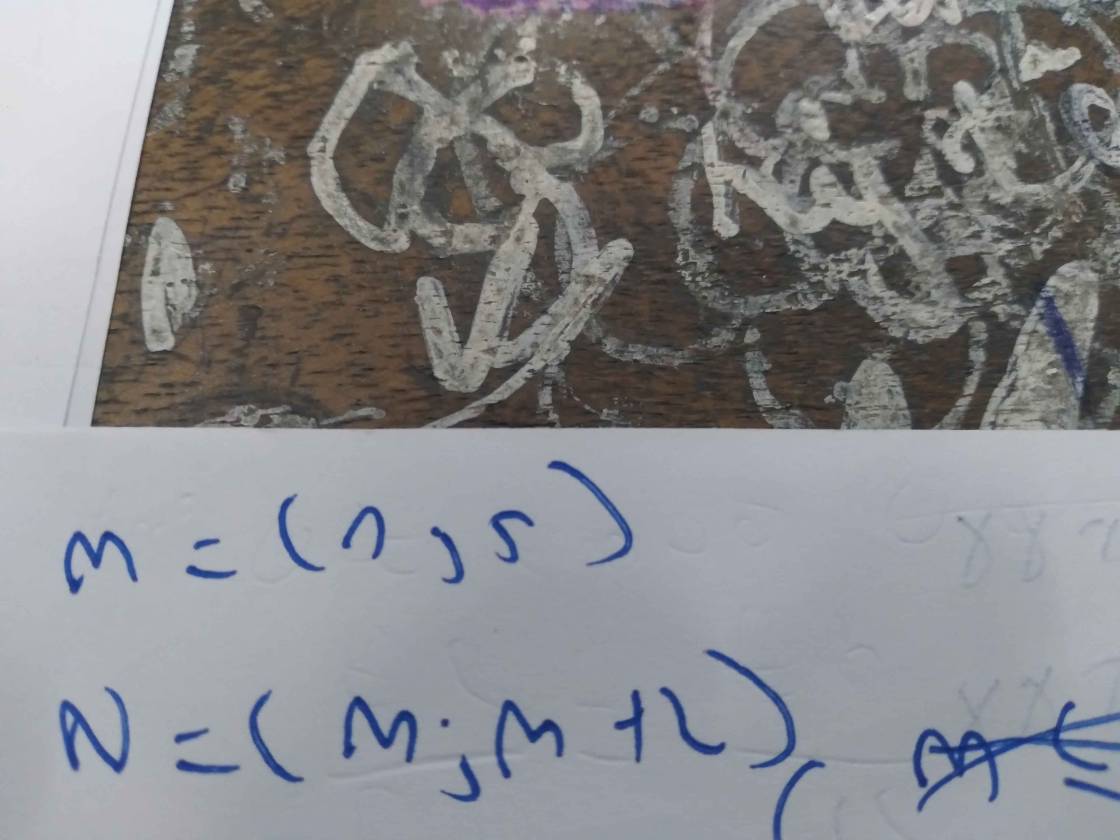Chương 1: MỆNH ĐỀ, TẬP HỢP

Số học sinh thích bóng chuyền hoặc bóng đá là: 

20 + 14 - 11 = 23 (học sinh)

Số học sinh không thích cả hai môn là: 

35 - 23 = 12 (học sinh)

Đáp số: ...

Số học sinh chỉ thích bóng đá : \(20-11=9\left(hs\right)\)

Số học sinh chỉ thích bóng chuyền : \(14-11=3\left(hs\right)\)

Tổng số học sinh thích ít nhất một trong hai môn (bao gồm cả những bạn thích cả hai môn): \(9+11+3=23\left(hs\right)\)

Số học sinh không thích cả hai môn: \(35-23=12\left(hs\right)\)

Lơ giải:

$\frac{1+5y}{5x}=\frac{1+7y}{4x}$

$\Rightarrow \frac{1+5y}{5}=\frac{1+7y}{4}$

$\Rightarrow 4(1+5y)=5(1+7y)$

$\Rightarrow 4+20y=5+35y$

$\Rightarrow 1=-15y\Rightarrow y=\frac{-1}{15}$

Có:

$\frac{1+5y}{5x}=\frac{1+3y}{12}$
$5x=(1+5y): \frac{1+3y}{12}=\frac{12(1+5y)}{1+3y}=\frac{12(1+5.\frac{-1}{15})}{1+3.\frac{-1}{15}}=10$

$\Rightarrow x=2$

Tham khảo
Hàm số chính là các quy tắc áp dụng trên các số. Nếu một đại lượng y phụ thuộc vào một đại lượng thay đổi x mà với một giá trị của x ta luôn xác định được một và chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x, và x gọi là biến số. Nói chung hàm số xuất hiện khi có một đại lượng số nào đó phụ thuộc vào một đại lượng số khác.

Định lí Pytago là một định lí trong hình tam giác vuông được đặt theo tên nhà toán học cổ đại Hy Lạp Pythagoras. Định lí nói rằng trong một tam giác vuông, bình phương của độ dài của cạnh huyền (đối diện góc vuông) bằng tổng của bình phương độ dài hai cạnh góc vuông, có công thức \(c^2=a^2+b^2\) (\(a\) và \(b\) là độ dài hai cạnh góc vuông, \(c\) là độ dài cạnh huyền.

\(\overrightarrow{AB}=\left(4m;2m\right)=\left(4;2\right)\)

=>VTPT là (-2;4)=(-1;2)

Phương trình đường thẳng AB là:

-1(x+2m)+2(y+m)=0

=>-x-2m+2y+2m=0

=>-x+2y=0

Thay x=0 và y=0 vào (AB), ta được:

\(-0+2\cdot0=0\)

=>0=0

=>(AB) luôn đi qua điểm O(0;0) với mọi \(m\ne0\)

Lời giải:

ĐK: $m\neq 0$ vì nếu $m=0$ thì $A\equiv B\equiv O$
$A(-2m, -m), B(2m, m)\Rightarrow \overrightarrow{AB}=(4m, 2m)$

$\Rightarrow VTPT của đt $AB$ là: $(-2m, 4m)$

PT đường thẳng AB:

$-2m(x+2m) + 4m(y+m)=0$

$\Leftrightarrow -2mx+4my=0$

Để $AB$ đi qua $O$ thì: $-2mx_O+4m.y_O=0$

$\Leftrightarrow -2m.0+4m.0=0$ (luôn đúng với mọi $m$)

Vậy với mọi $m\neq 0; m\in\mathbb{R}$ thì AB luôn đi qua $O$.

Điểm $M$ là điểm nào vậy bạn? Bạn xem lại đề xem đã viết chuẩn chưa vậy?

20. A

21. Đề không có đáp án đúng. Đáp án đúng phải là \(A\cap B=\left\{c;m\right\}\).

22. \(\left\{{}\begin{matrix}\left|k\right|\le3\\k\in Z\end{matrix}\right.\Rightarrow k\in\left\{-3;-2;-1;0;1;2;3\right\}\)

\(\Rightarrow A=\left\{3;5;11;21\right\}\)

Chọn D.

23. B.