Số nghiệm của phương trình \(\left(x+3\right)\sqrt{2x^2+1}=x^2+x+3\) là.
Mọi người giải chi tiết giúp em với ạ.
Số nghiệm của phương trình \(\left(x+3\right)\sqrt{2x^2+1}=x^2+x+3\) là.
Mọi người giải chi tiết giúp em với ạ.
\(\Leftrightarrow\left(x+3\right)\sqrt{2x^2+1}-\left(x+3\right)=x^2\)
=>\(\left(x+3\right)\cdot\left(\sqrt{2x^2+1}-1\right)=x^2\)
=>\(\left(x+3\right)\cdot\dfrac{2x^2+1-1}{\sqrt{2x^2+1}+1}-x^2=0\)
=>\(x^2\left(\dfrac{2\left(x+3\right)}{\sqrt{2x^2+1}+1}-1\right)=0\)
=>x^2=0 hoặc \(\dfrac{2\left(x+3\right)}{\sqrt{2x^2+1}+1}=1\)
=>\(\left[{}\begin{matrix}x=0\\\sqrt{2x^2+1}+1=2x+6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\2x^2+1=\left(2x+5\right)^2;x>=-\dfrac{5}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\4x^2+20x+25-2x^2-1=0;x>=-\dfrac{5}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\\left\{{}\begin{matrix}2x^2+20x+24=0\\x>=-\dfrac{5}{2}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5+\sqrt{13}\end{matrix}\right.\)
=>Phương trình này có 2 nghiệm
Giải phương trình: \(x^2+2\sqrt{2x+7}=2\sqrt{-2x+3}+5\)
ĐKXĐ: \(\left\{{}\begin{matrix}2x+7>=0\\-2x+3>=0\end{matrix}\right.\Leftrightarrow-\dfrac{7}{2}< =x< =\dfrac{3}{2}\)
PT\(\Leftrightarrow x^2-1+2\sqrt{2x+7}=2\sqrt{-2x+3}+4\)
=>\(\left(x-1\right)\left(x+1\right)+2\sqrt{2x+7}-6=2\sqrt{-2x+3}-2\)
=>\(\left(x-1\right)\left(x+1\right)+2\cdot\dfrac{2x+7-9}{\sqrt{2x+7}+3}=2\cdot\dfrac{-2x+3-1}{\sqrt{-2x+3}+1}\)
=>\(\left(x-1\right)\left(x+1\right)+\dfrac{4\left(x-1\right)}{\sqrt{2x+7}+3}-2\cdot\dfrac{-2\left(x-1\right)}{\sqrt{-2x+3}+1}=0\)
=>\(\left(x-1\right)\left(x+1+\dfrac{4}{\sqrt{2x+7}+3}+\dfrac{4}{\sqrt{-2x+3}+1}\right)=0\)
=>x-1=0
=>x=1(nhận)
Các bạn giúp mình với ạ!!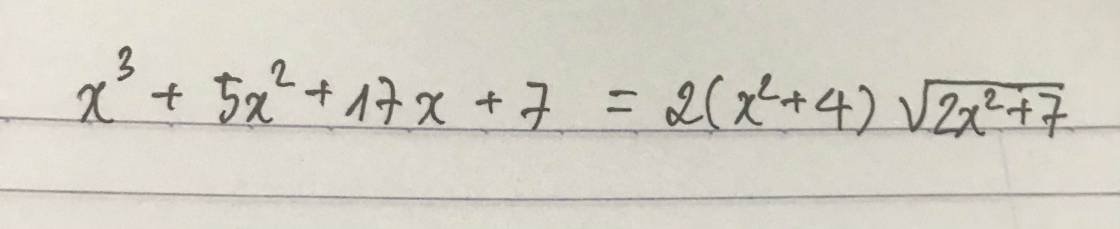
khai triển và rút gọn biểu thức B = (1- căn3)^5
khai triển và rút gọn biểu thức A = (2+ căn 2)^4
√𝑥2+𝑚 − √2𝑥2+2𝑥+𝑚=0 với 𝑚 là STT
=>\(\dfrac{x^2+m-2x^2-2x-m}{\sqrt{x^2+m}+\sqrt{2x^2+2x+m}}=0\)
=>\(\dfrac{-x^2-2x}{\sqrt{x^2+m}+\sqrt{2x^2+2x+m}}=0\)
=>-x^2-2x=0
=>x=0 hoặc x=-2
\(\Leftrightarrow\left(x-3\right)\left(\sqrt{x^2+4}-\left(x+3\right)\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x^2+4=x^2+6x+9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{6}\end{matrix}\right.\)
Giải bất phương trình sau:
\(\dfrac{1}{\sqrt{2x^2+3x-5}}\) ≥ \(\dfrac{1}{2x-1}\)