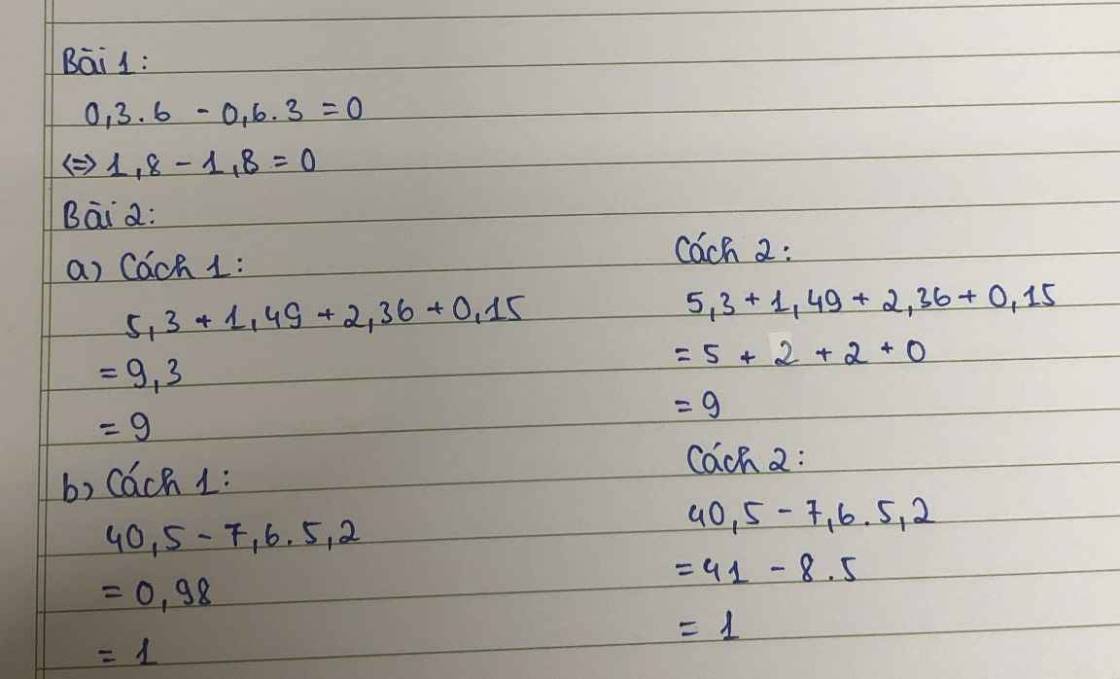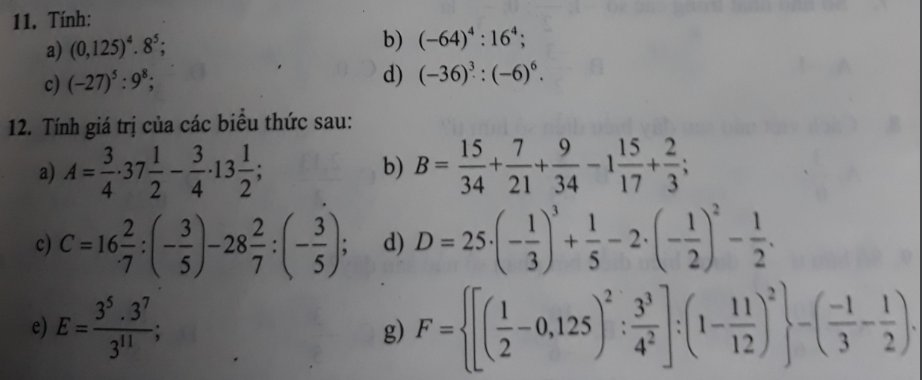Bài 9: Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn

CHÚC EM HỌC TỐT NHÁ

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có

AB=AC

góc BAD chung

=>ΔABD=ΔACE

b: ΔABD=ΔACE

=>AD=AE
=>ΔADE cân tại A

c: Xét ΔADO vuông tại D và ΔAEO vuông tại E có

AO chung

AD=AE
=>ΔADO=ΔAEO

=>DO=EO

mà AD=AE
nên AO là trung trực của DE

a) ................................. =) ABD = ACE

b) ................................. =) AED cân

c) ................................. =) AO là đường trung trực của ED

d) ................................. =) \(\widehat{ECB}\) = \(\widehat{DKC}\) 

Bài 4:

a) \(\left(12x^4+4x^3-2x\right):2x\)

\(=2x\cdot\left(6x^3+2x^2-1\right):2x\)

\(=6x^3+2x^2-1\)

b) \(\left(2x-1\right)\left(3x^2+2x-5\right)\)

\(=2x\left(3x^2+2x-5\right)-\left(3x^2+2x-5\right)\)

\(=6x^3+4x^2-10x-3x^2-2x+5\)

\(=6x^3+x^2-12x+5\)

c) \(\left(15x^4+6x^3-9x\right):3x\)

\(=3x\cdot\left(5x^3+2x^2-3\right):3x\)

\(=5x^3+2x^2-3\)

d) \(\left(5x-1\right)\left(x^2+2x-6\right)\)

\(=5x\left(x^2+2x-6\right)-\left(x^2+2x-6\right)\)

\(=5x^3+10x^2-30x-x^2-2x+6\)

\(=5x^3+9x^2-32x+6\)

Bài 5:

(1) 

a) \(A\left(x\right)+B\left(x\right)\)

\(=2x^2-x^3+3x+3+x^3-x^2-4-3x\)

\(=x^2-1\)

\(A\left(x\right)-B\left(x\right)\)

\(=2x^2-x^3+3x+3-x^3+x^2+4+3x\)

\(=3x^2-2x^3+6x+7\)

b) Ta có:

\(A\left(x\right)+B\left(x\right)=x^2-1\)

Mà: \(x^2-1=0\)

\(\Rightarrow x^2+x-x-1=0\)

\(\Rightarrow x\left(x+1\right)-\left(x+1\right)=0\)

\(\Rightarrow\left(x-1\right)\left(x+1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

(2) 

a) \(A\left(x\right)+B\left(x\right)\)

\(=3x^2-2x^3+4x+1+2x^3-2x^2-5-4x\)

\(=x^2-4\)

 \(A\left(x\right)-B\left(x\right)\)

\(=3x^2-2x^3+4x+1-2x^3+2x^2+5+4x\)

\(=5x^2-4x^3+8x+6\)

b) Ta có:

\(A\left(x\right)+B\left(x\right)=0\)

\(\Rightarrow x^2-4=0\)

\(\Rightarrow x^2-2x+2x-4=0\)

\(\Rightarrow x\left(x-2\right)+2\left(x-2\right)=0\)

\(\Rightarrow\left(x-2\right)\left(x+2\right)=0\)

\(\Rightarrow\left\{{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

Bài 1

a) P(x) = 5x⁵ - 7x² + 3x³ - 2x⁵ - 4x - 3x⁵

= (5x⁵ - 2x⁵ - 3x⁵) + 3x³ - 7x² - 4x

= 3x³ - 7x² - 4x

Q(x) x³ + 5x - 6 - 3x³

= (x³ - 3x³) + 5x - 6

= -2x³ + 5x - 6

b) P(x) + Q(x) = (3x³ - 7x² - 4x) + (-2x³ + 5x - 6)

= 3x³ - 7x² - 4x - 2x³ + 5x - 6

= (3x³ - 2x³) - 7x² + (-4x + 5x) - 6

= x³ - 7x² + x - 6

P(x) - Q(x) = (3x³ - 7x² - 4x) - (-2x³ + 5x - 6)

= 3x³ - 7x² - 4x + 2x³ - 5x + 6

= (3x³ + 2x³) - 7x² + (-4x - 5x) + 6

= 5x³ - 7x² - 9x + 6

c) P(0) = 3.0³ - 7.0² - 4.0 = 0

⇒ x = 0 là một nghiệm của P(x)

Q(0) = -2.0³ + 5.0 - 6 = -6

⇒ x = 0 không là nghiệm của Q(x)

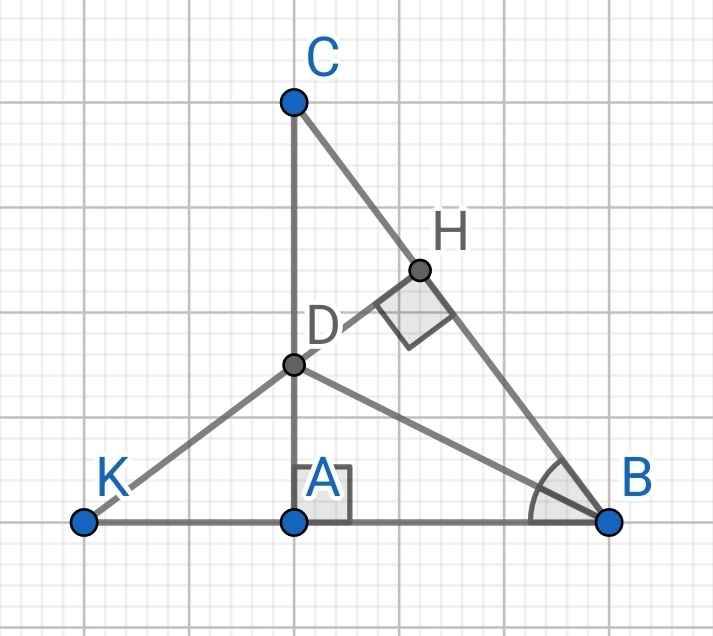 a) Do BD là tia phân giác của ∆ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠HBD

Xét hai tam giác vuông: ∆ABD và ∆HBD có:

BD chung

∠ABD = ∠HBD (cmt)

⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)

⇒ AD = HD (hai cạnh tương ứng)

b) ∆ADK vuông tại A

DK là cạnh huyền nên là cạnh lớn nhất

⇒ AD < DK

Mà AD = HD (cmt)

⇒ DH < DK

c) Xét hai tam giác vuông: ∆DAK và ∆DHC có:

AD = HD (cmt)

∠ADK = ∠HDC (đối đỉnh)

∆DAK = ∆DHC (cạnh góc vuông - góc nhọn kề)

⇒ AK = HC (hai cạnh tương ứng)

Do ∆ABD = ∆HBD (cmt)

⇒ AB = HB (hai cạnh tương ứng)

Mà AK = HC (cmt)

⇒ AB + AK = HB + HC

⇒ BK = BC

∆KBC có BK = BC (cmt)

⇒ ∆KBC cân tại B

Câu 12:

\(\left(2x^3+4x^2-16x\right):2x\)

\(=2x\cdot\left(x^2+2x-8\right):2x\)

\(=x^2+2x-8\)

⇒ A

Tự luận:

Câu 1:

a) \(5x+3x-12x\)

\(=8x-12x\)

\(=-4x\)

b) \(2x\left(x-5\right)\)

\(=2x^2-10x\)

c) \(\left(x-3\right)\left(x+4\right)\)

\(=x^2+4x-3x-12\)

\(=x^2+x-12\)

d) \(\left(4x^2-5x-6\right):\left(x-2\right)\)

\(=\left(4x^2+3x-8x-6\right):\left(x-2\right)\)

\(=\left[x\left(4x+3\right)-2\left(4x+3\right)\right]:\left(x-2\right)\)

\(=\left(x-2\right)\left(4x+3\right):\left(x-2\right)\)

\(=4x+3\)

Câu 2:

\(A=\left(x-3\right)\left(x+2\right)+\left(x-4\right)\left(x+4\right)-\left(2x-1\right)x\)

\(A=x^2+2x-3x-6+x^2+4x-4x-16-2x^2+x\)

\(A=\left(x^2+x^2-2x^2\right)+\left(2x-3x+4x-4x+x\right)-\left(6+16\right)\)

\(A=-22\)

Vậy giác trị của A không phụ thuộc vào biến

Câu 12:

\(\dfrac{2x^3+4x^2-16x}{2x}\\ =\dfrac{2x^3}{2x}+\dfrac{4x^2}{2x}-\dfrac{16x}{2x}\\ =x^2+2x-8\)

Vậy chọn A

Tự luận:

Câu 1:

a)

\(5x+3x-12x\\ =\left(5+3-12\right)x=-4x\)

b)

\(2x\left(x-5\right)\\ =2x.x-2x.5\\ =4x^2-10x\)

c)

\(\left(x-3\right)\left(x+4\right)\\ =x.x+x.4-3.x-3.4\\ =x^2+4x-3x-12\\ =x^2+x-12\)

d)

\(\dfrac{4x^2-5x-6}{x-2}\\ =\dfrac{4x^2+3x-8x-6}{x-2}\\ =\dfrac{x\left(4x+3\right)-2\left(4x+3\right)}{\left(x-2\right)}\\ =\dfrac{\left(x-2\right)\left(4x+3\right)}{x-2}\\ =4x+3\)

khó thế

Câu 1: Hệ số tự do của đa thức N(x) là: \(5\)

⇒ Chọn B

Câu 2: Trọng tâm là giao điểm của 3 đường trung tuyến

⇒ Chọn D

Câu 3: Đơn thức là: \(8x^5\)

⇒ Chọn C

Câu 4:

\(\dfrac{x+3}{5}=\dfrac{x-1}{7}\)

\(\Rightarrow7\left(x+3\right)=5\left(x-1\right)\Rightarrow7x+21=5x-5\)

\(\Rightarrow2x=-5-21\)

\(\Rightarrow2x=-26\Rightarrow x=\dfrac{-26}{2}=-13\)

⇒ Chọn D

Câu 5: 

Ta có:

\(x=3y\) và \(x+y=8\) thay vào ta có:

\(\Rightarrow3y+y=8\Rightarrow4y=8\)

\(\Rightarrow y=\dfrac{8}{4}=2\)

Vậy: \(x=3\cdot2=6\)

⇒ Chọn A

Câu 6: Đa thức M(x) có bậc 4: 

⇒ Chọn C

Câu 7: BC > CA > AB

\(\Rightarrow\widehat{A}>\widehat{B}>\widehat{C}\)

⇒ Chọn C

Câu 8: 

Độ dài 3 cạnh của tam giác là:  20cm, 12cm, 16cm

⇒ Chọn A

Câu 9: \(\left|x-2\right|=3\)

\(\Rightarrow\left\{{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)

⇒ Chọn D

Câu 10: 

\(BG=\dfrac{2}{3}\cdot MB=\dfrac{2}{3}\cdot36=24\left(cm\right)\)

⇒ Chọn C

Câu 11:

\(P\left(x\right)=0\)

\(\Rightarrow5x^2-4+2x-5x^2=0\)

\(\Rightarrow2x=4\)

\(\Rightarrow x=\dfrac{4}{2}=2\)

⇒ Chọn B

khó thế

\(0,\left(4\right)=\dfrac{4}{9}\)

0,(571428) = 571428/999999 = 4/7

2,01(6) = 2,01 + 6/900 = 121/60

0,1(63) = 0,1 + 63/990 = 9/55

2,41(3) = 2,41 + 3/900 = 181/75

0,88(63) = 0,88 + 63/9900 = 39/44

12:

a: =3/4(37+1/2-13-1/2)

=24*3/4=18

b: \(=\dfrac{15}{34}+\dfrac{9}{34}-1-\dfrac{15}{17}+\dfrac{1}{3}+\dfrac{2}{3}\)

=24/34-15/17

=12/17-15/17=-3/17

c: \(=\dfrac{-5}{3}\left(16+\dfrac{2}{7}-28-\dfrac{2}{7}\right)=-12\cdot\dfrac{-5}{3}=20\)

d: \(=25\cdot\dfrac{-1}{27}+\dfrac{1}{5}-2\cdot\dfrac{1}{4}-\dfrac{1}{2}\)

=-25/27+1/5-1

=-25/27-4/5

=-125/135-108/135=-233/135

e: =3^12/3^11=3

f: \(=\left\{\left[\left(\dfrac{1}{2}-\dfrac{1}{8}\right)^2\cdot\dfrac{4^2}{3^3}\right]:\left(\dfrac{1}{12}\right)^2\right\}-\dfrac{-5}{6}\)

\(=\left\{\left[\dfrac{3^2}{8^2}\cdot\dfrac{4^2}{3^3}\right]\cdot144\right\}+\dfrac{5}{6}\)

\(=12+\dfrac{5}{6}=\dfrac{77}{6}\)

Đề bài đâu em hi?

lỗi?