Bài 9: Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
Nội dung lý thuyết
Các phiên bản khác1. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
Ta xét các ví dụ sau:
Ví dụ 1: Viết các phân số \(\dfrac{3}{20}\), \(\dfrac{37}{25}\), \(\dfrac{23}{40}\) dưới dạng số thập phân.
Ở lớp dưới, ta đã biết quy tắc chia một số tự nhiên cho một số tự nhiên. Sau đây, ta sẽ áp dụng quy tắc đó để biến đổi một phân số về dạng số thập phân.
Ta có:
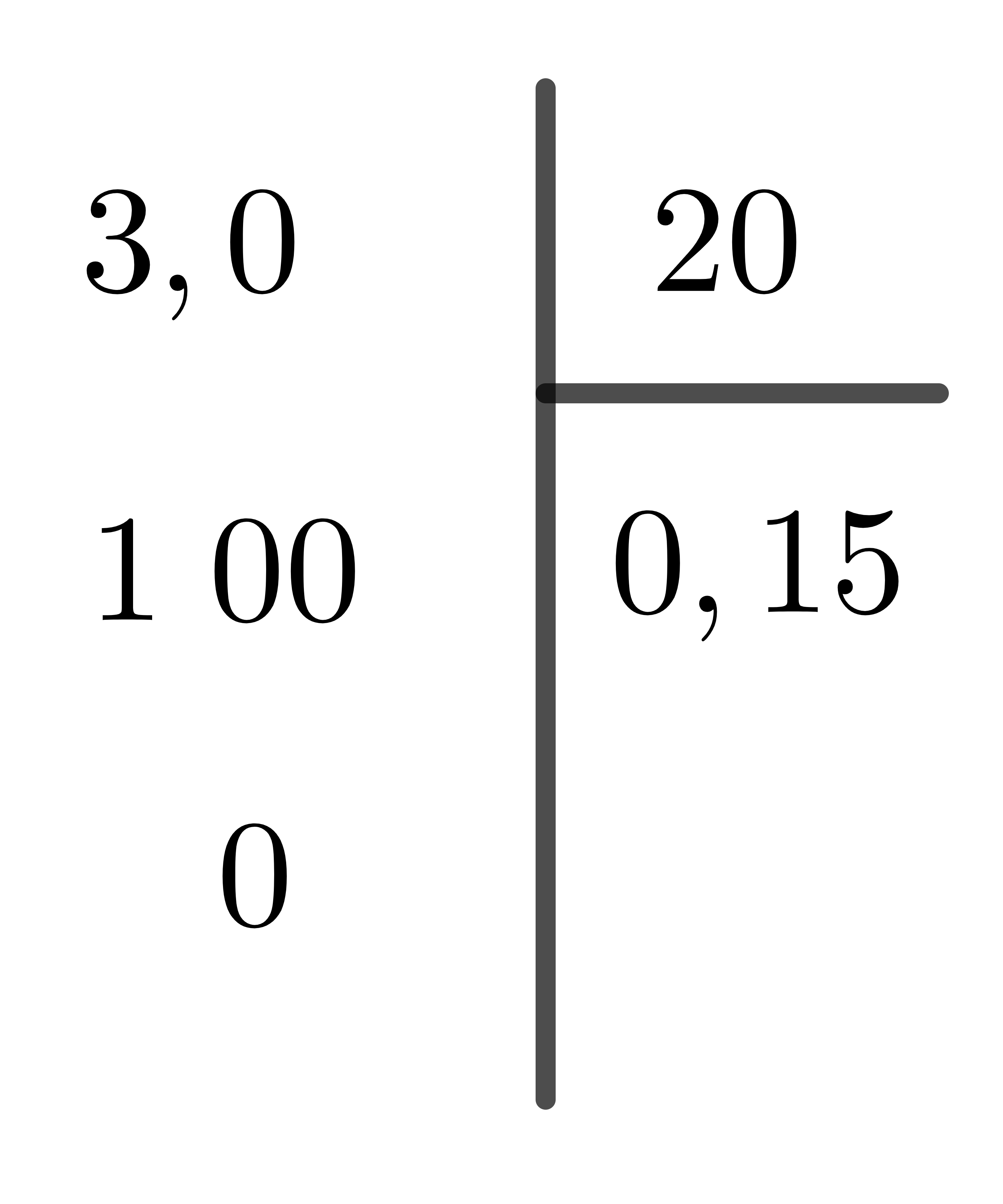


Như vậy, ta có thể viết các phân số trên dưới dạng số thập phân như sau:
\(\dfrac{3}{20}=0,15;\)
\(\dfrac{37}{25}=1,48;\)
\(\dfrac{23}{40}=0,575.\)
Các số \(0,15;1,48;0,575\) trong ví dụ trên được gọi là số thập phân hữu hạn.
Ví dụ 2: Viết số \(\dfrac{5}{12}\) dưới dạng số thập phân.
Ta thực hiện tương tự như trên với quy tắc chia hai số tự nhiên:

Dễ thấy, phép chia trên không bao giờ chấm dứt. Nếu tiếp tục thực hiện chia thì chữ số \(6\) trong thương sẽ lặp đi lặp lại.
Ta nói: khi chia \(5\) cho \(12\), ta được số \(0,4166...\)
Ta gọi số \(0,4166...\) là một số thập phân vô hạn tuần hoàn và có thể viết gọn là \(0,41\left(6\right).\)
Kí hiệu \(\left(6\right)\) chỉ rằng chữ số \(6\) được lặp lại vô hạn lần. Số \(6\) được gọi là chu kì của số thập phân vô hạn tuần hoàn \(0,41\left(6\right)\).
Ví dụ:
+) \(\dfrac{1}{9}=0,1111...=0,\left(1\right)\). Số \(0,\left(1\right)\) là số thập phân vô hạn tuần hoàn với chu kì \(1\).
+) \(\dfrac{1}{90}=0,0111...=0,0\left(1\right)\). Số \(0,0\left(1\right)\) cũng là một số thập phân vô hạn tuần hoàn với chu kì \(1\).
+) \(\dfrac{-17}{11}=-1,545454...=-1,\left(54\right)\). Đây là một số thập phân vô hạn tuần hoàn với chu kì \(54\).
Chú ý: Một cách trực quan, ta có thể thấy:
- Số thập phân hữu hạn có phần thập phân chỉ có số chữ số nhất định. Còn phần thập phân của số thập phân vô hạn tuần hoàn có vô số chữ số và các chữ số đó lặp lại theo một quy luật nhất định, gọi là chu kì.
- Chu kì của số thập phân vô hạn tuần hoàn có thể có một hoặc nhiều chữ số.
Nhận xét: Ta có thể viết một phân số dưới dạng số thập phân bằng cách thực hiện phép chia tử số cho mẫu số. Chẳng hạn:
+) \(\dfrac{1}{4}=0,25.\)
+) \(\dfrac{1}{3}=0,333...=0,\left(3\right).\)
+) \(\dfrac{-13}{15}=-0,8666...=-0,8\left(6\right).\)
+) \(\dfrac{-14}{33}=-0,424242...=-0,\left(42\right).\)
2. Nhận xét
Ở các ví dụ phía trên, ta thấy: Có những phân số viết được dưới dạng số thập phân hữu hạn, cũng có những phân số lại viết được dưới dạng số thập phân vô hạn tuần hoàn. Câu hỏi đặt ra là những phân số như thế nào sẽ được biểu diễn bởi từng trường hợp đó?
Người ta đã chứng minh được kết quả sau:
- Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác \(2\) và \(5\) thì phân số đó viết được dưới dạng số thập phân hữu hạn.
- Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác \(2\) và \(5\) thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.
Ví dụ:
+) Xét phân số \(\dfrac{-3}{40}\). Ta có: \(40=2^3.5\), do đó nó chỉ có hai ước nguyên tố là \(2\) và \(5\). Dựa vào nhận xét trên, ta có thể suy ra \(\dfrac{-3}{40}\) viết được dưới dạng số thập phân hữu hạn. Thật vậy: \(\dfrac{-3}{40}=-0,075\).
+) Xét phân số \(\dfrac{10}{72}\). Ta có: \(\dfrac{10}{72}=\dfrac{5}{36}\), \(36=2^2.3^2\), do đó nó có hai ước nguyên tố là \(2\) và \(3\). Dựa vào nhận xét trên, ta có thể suy ra \(\dfrac{5}{36}\) viết được dưới dạng số thập phân vô hạn tuần hoàn. Thật vậy: \(\dfrac{10}{72}=\dfrac{5}{36}=0,13888...=0,13\left(8\right)\).
Nhận xét: Để viết một phân số về dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn, trước tiên ta cần đưa phân số về dạng tối giản, sau đó mới phân tích mẫu số thành tích các số nguyên tố.
Ví dụ: Trong các phân số \(\dfrac{3}{16}\), \(\dfrac{-67}{80}\), \(\dfrac{29}{60}\), \(\dfrac{-33}{56}\), phân số nào viết được dưới dạng số thập phân hữu hạn, phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn?
Lời giải:
+) Ta có: \(16=2^4\) nên nó chỉ có ước nguyên tố là \(2\)
\(\Rightarrow\dfrac{3}{16}\) viết được dưới dạng số thập phân hữu hạn.
+) Ta có \(80=2^4.5\) nên nó có ước nguyên tố là \(2\) và \(5\)
\(\Rightarrow\dfrac{-67}{80}\) viết được dưới dạng số thập phân hữu hạn.
+) Ta có \(60=2.3.5\), do đó nó có ước nguyên tố là \(2,3,5\)
\(\Rightarrow\dfrac{29}{60}\) viết được dưới dạng số thập phân vô hạn tuần hoàn.
+) Ta có \(56=2^3.7\) nên nó có ước nguyên tố là \(2,7\)
\(\Rightarrow\dfrac{-33}{56}\) viết được dưới dạng số thập phân vô hạn tuần hoàn.
@948513@
Chú ý: Dễ thấy, mỗi số thập phân hữu hạn là một số hữu tỉ. Người ta cũng chứng minh được rằng: Mỗi số thập phân vô hạn tuần hoàn cũng là một số hữu tỉ.
Chẳng hạn:
+) \(0,\left(7\right)=0,\left(1\right).7=\dfrac{1}{9}.7=\dfrac{7}{9};\)
+) \(0,\left(31\right)=0,\left(01\right).31=\dfrac{1}{90}.31=\dfrac{31}{90};\)
+) \(-1,4\left(2\right)=-\left(1,4+0,0\left(2\right)\right)=-\left(1,4+0,0\left(1\right).2\right)=-\left(\dfrac{7}{5}+\dfrac{1}{90}.2\right)=\dfrac{-64}{45}.\)
@948590@
Tổng quát, ta có kết luận sau:
Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn. Ngược lại, mỗi số thập phân hữu hạn hoặc vô hạn tuần hoàn biểu diễn một số hữu tỉ.