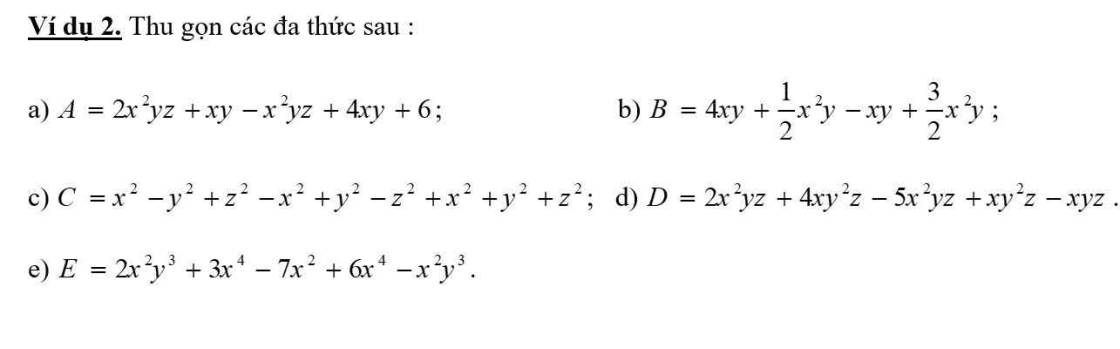a, (2x+1)^2+2(2x+1)+1 b, (3x-2y)^2+4(3x-2y)+4 c,(2x+1)^2 d,(x^2+2)^2 e, (2x+3y)^2 f, (x-3)(x+3)
Bài 4: Những hằng đẳng thức đáng nhớ (Tiếp)
`a,` `(2x+1)^2+2(2x+1)+1 = (2x+1+1)^2 = (2x+2)^2`
`b,` `(3x-2y)^2+4(3x-2y)+4 = (3x-2y+2)^2`
`c,` `(2x+1)^2 = (2x)^2 + 2*2x*1 + 1^2 = 4x^2 + 4x + 1`
`d,` `(x^2+2)^2 = (x^2)^2 + 2*x^2*2 + 2^2 = x^4 + 4x^2 + 4`
`e,` `(2x+3y)^2 = (2x)^2 + 2*2x*3y + (3y)^2 = 4x^2 + 12xy + 9y^2`
`f,` `(x-3)(x+3) = x^2 - 3^2 = x^2 - 9`
Đúng 1
Bình luận (0)
a,x^2-4=0 b,(x-1)^2-2(x-1)=0 c, 16x^2-9=0 d, (x+2)^2-(x-3)(x+3)=32 e, (x-1)^2-x^2-4x-4=0 f, (2x+1)^2-4(x-1)(x+1)=0
a: \(x^2-4=0\)
=>\(x^2=4\)
=>\(\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
b: \(\left(x-1\right)^2-2\left(x-1\right)=0\)
=>(x-1)(x-1-2)=0
=>(x-1)(x-3)=0
=>\(\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
c: \(16x^2-9=0\)
=>\(16x^2=9\)
=>\(x^2=\dfrac{9}{16}\)
=>\(\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=-\dfrac{3}{4}\end{matrix}\right.\)
d: \(\left(x+2\right)^2-\left(x-3\right)\left(x+3\right)=32\)
=>\(x^2+4x+4-\left(x^2-9\right)=32\)
=>4x+13=32
=>4x=32-13=19
=>\(x=\dfrac{19}{4}\)
e: \(\left(x-1\right)^2-x^2-4x-4=0\)
=>\(x^2-2x+1-x^2-4x-4=0\)
=>-6x-3=0
=>-6x=3
=>\(x=-\dfrac{3}{6}=-\dfrac{1}{2}\)
f: \(\left(2x+1\right)^2-4\left(x-1\right)\left(x+1\right)=0\)
=>\(4x^2+4x+1-4\left(x^2-1\right)=0\)
=>\(4x^2+4x+1-4x^2+4=0\)
=>4x=-5
=>\(x=-\dfrac{5}{4}\)
Đúng 1
Bình luận (0)
`a, x^2 - 4=0`
`=> x^2=4`
`=>x^2=(+-2)^2`
`=> x=+-2`
Vậy: `x=+-2`
`b, (x-1)^2 - 2(x-1)=0`
`=> (x-1-2)(x-1)=0`
`=> (x-3)(x-1)=0`
`=> [(x-3=0),(x-1=0):}`
`=> [(x=3),(x=1):}`
Vậy: `x=3;x=1`
`c, 16x^2 - 9 = 0`
`=> 16x^2=9`
`=> x^2=9/16`
`=> x^2=(+-3/4)^2`
`=> x=+-3/4`
Vậy: `x=+-3/4`
`d, (x+2)^2 - (x-3)(x+3) = 32`
`=>(x+2)^2 - (x^2 - 9) = 32`
`=> x^2+4x+4-x^2+9=32`
`=> 4x+13=32`
`=> 4x=19`
`=> x=19/4`
Vậy: `x=19/4`
Đúng 1
Bình luận (0)
a, x^2-6x+9 b, 4x^2+4x+1 c, 1/4a^2+2ab+4b^2 d, 1/9-2/3y^4+y^8 e, 9x^2-15x+25/4 g, 36X^4+9x^2y+1/4y^2
`a, x^2-6x+9`
`= x^2-2*x*3+3^2`
`= (x-3)^2`
`b, 4x^2 + 4x+1`
`= (2x)^2 + 2*2x*1+1^2`
`= (2x+1)^2`
`c, 1/4a^2+2ab+4b^2`
`= (1/2a)^2 + 2*1/2a*2b+(2b)^2`
`= (1/2a+2b)^2`
`d, 1/9-2/3y^4+y^8`
`= y^8-2/3y^4+1/9`
`= (y^4)^2 - 2*y^4*1/3+(1/3)^2`
`= (y^4-1/3)^2`
Đúng 2
Bình luận (0)
a) x² - 6x + 9
= x² - 2.x.3 + 3²
= (x - 3)²
b) 4x² + 4x + 1
= (2x)² + 2.2x.1 + 1²
= (2x + 1)²
c) Sửa đề:

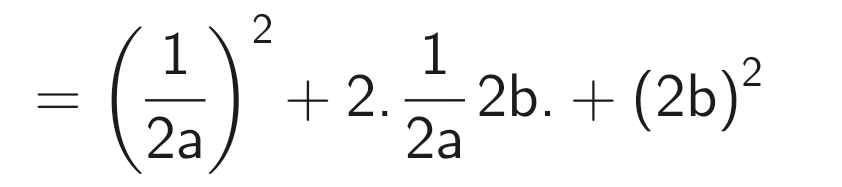
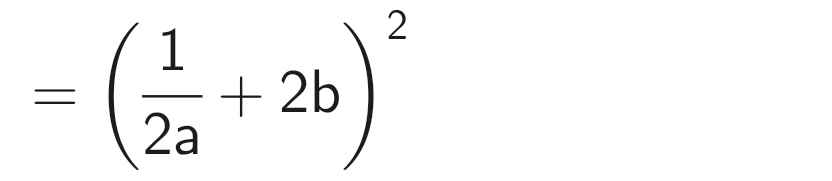
d)

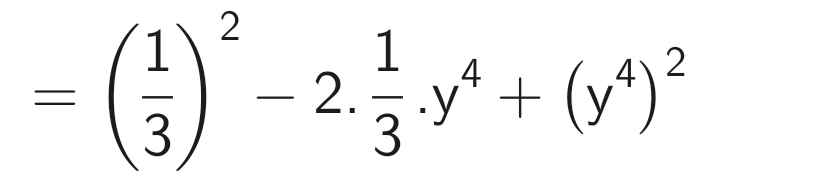
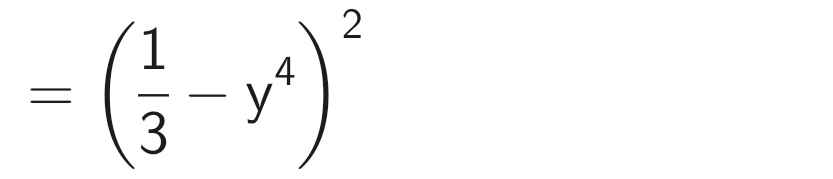
Đúng 2
Bình luận (0)
`e, 9x^2 - 15x + 25/4`
`= (3x)^2 - 2*3x*5/2+(5/2)^2`
`= (3x-5/2)^2`
Sửa: `g, 36x^4 + 6x^2y + 1/4y^2`
`= (6x^2)^2 + 2*6x^2*1/2y+(1/2y)^2`
`= (6x^2+1/2y)^2`
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
x4-2xy6
\(x^4-2xy^6\)
\(=x\cdot x^3-x\cdot2y^6\)
\(=x\left(x^3-2y^6\right)\)
Đúng 0
Bình luận (0)
Trả lời giúp mình câu 28 chỉ cần đáp án kh cần cách giải ạ
a: \(A=2x^2yz-x^2yz+xy+4xy+6=x^2yz+5xy+6\)
b: \(B=\dfrac{1}{2}x^2y+\dfrac{3}{2}x^2y+4xy-xy=2x^2y+3xy\)
c: \(C=x^2+x^2-x^2+y^2-y^2+y^2+z^2-z^2+z^2\)
\(=x^2+y^2+z^2\)
d: \(D=2x^2yz-5x^2yz+4xy^2z+xy^2z-xyz\)
\(=-3x^2yz+5xy^2z-xyz\)
e: \(E=2x^2y^3-x^2y^3+3x^4+6x^4-7x^2\)
\(=9x^4-7x^2+x^2y^3\)
Đúng 1
Bình luận (0)
Thu gọn biểu thức sau
x(x-1)(x+1)-(x-3)(x+2x+9)
(ngay chỗ x+2x thì x có mũ 2 ạ)
em cần rất gấp ạ
\(x(x-1)(x+1)-(x-3)(x^2+2x+9)\)
\(=x\left(x^2-1\right)-\left[x\left(x^2+2x+9\right)-3\left(x^2+2x+9\right)\right]\)
\(=x^3-x-\left(x^3+2x^2+9x-3x^2-6x-27\right)\)
\(=x^3-x-\left(x^3-x^2+3x-27\right)\)
\(=x^3-x-x^3+x^2-3x+27\)
\(=x^2-4x+27\)
#\(Toru\)
Đúng 3
Bình luận (1)
 làm cả 3 bài giúp ạ
làm cả 3 bài giúp ạ
Bài 16
a) x² + 2x + 2
= x² + 2x + 1 + 1
= (x + 1)² + 1
Do (x + 1)² ≥ 0 với mọi x ∈ R
⇒ (x + 1)² + 1 > 0 với mọi x ∈ R
b) 9a² - 6a + 3
= 9a² - 6a + 1 + 2
= (3a - 1)² + 2
Do (3a - 1)² ≥ 0 với mọi a ∈ R
⇒ (3a - 1)² + 2 > 0 với mọi a ∈ R
Đúng 1
Bình luận (0)
Bài 17
M = y² + 6y + 7
= y² + 6y + 9 - 2
= (y + 3)² - 2
(y + 3)² ≥ 0 với mọi y ∈ R
⇒ (y + 3)² - 2 ≥ -2 với mọi y ∈ R
Vậy GTNN của M là -2 khi y = -3
------------
H = 16b² - 16b + 5
= 16b² - 16 + 4 + 1
= (4b - 2)² + 1
Do (4b - 2)² ≥ 0 với mọi b ∈ R
⇒ (4b - 2)² + 1 ≥ 1 với mọi b ∈ R
Vậy GTNN của H là 1 khi b = 1/2
------------
T = x² + y² + 2x + 1 - 2y
= x² + 2x + 1 + y² - 2y + 1 - 1
= (x + 1)² + (y - 1)² - 1
Do (x + 1)² ≥ 0 với mọi x ∈ R
(y - 1)² ≥ 0 với mọi y ∈ R
⇒ (x + 1)² + (y - 1)² ≥ 0 với mọi x, y ∈ R
⇒ (x + 1)² + (y - 1)² - 1 ≥ -1 với mọi x, y ∈ R
Vậy GTNN của T là -1 khi x = -1; y = 1
Đúng 1
Bình luận (5)
Bài 18
a) -x² + 6x - 12
= -(x² - 6x + 12)
= -(x² - 6x + 9 + 3)
= -(x - 3)² - 3
Do (x - 3)² ≥ 0 với mọi x ∈ R
⇒ -(x - 3)² ≤ 0 với mọi x ∈ R
⇒ -(x - 3)² - 3 < 0 với mọi x ∈ R
b) -9y² + 6y - 3
= -(9y² - 6y + 3)
= -(9y² - 6y + 1 + 2)
= -(3y - 1)² - 2
Do (3y - 1)² ≥ 0 với mọi y ∈ R
⇒ -(3y - 1)² ≤ 0 với mọi y ∈ R
⇒ -(3y - 1)² - 2 < 0 với mọi y ∈ R
Đúng 2
Bình luận (0)
Chia mot hinh vuong thanh cac hinh vuong va hinh chu nhat .tinh dien tich moi hinh vuong va hinh moi hinh chu nhat duoc chia theo x va y .tinh tong cua chung va phan tich ket qua vua tim duoc thanh nhan tu.
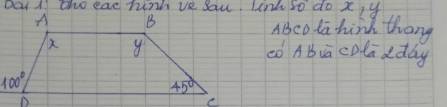
góc ADC=180-100=80 độ
AB//CD
=>góc DAB+góc ADC=180 độ và góc ABC+góc BCD=180 độ
=>x=180-80=100 độ và y=180-45=135 độ
Đúng 1
Bình luận (0)