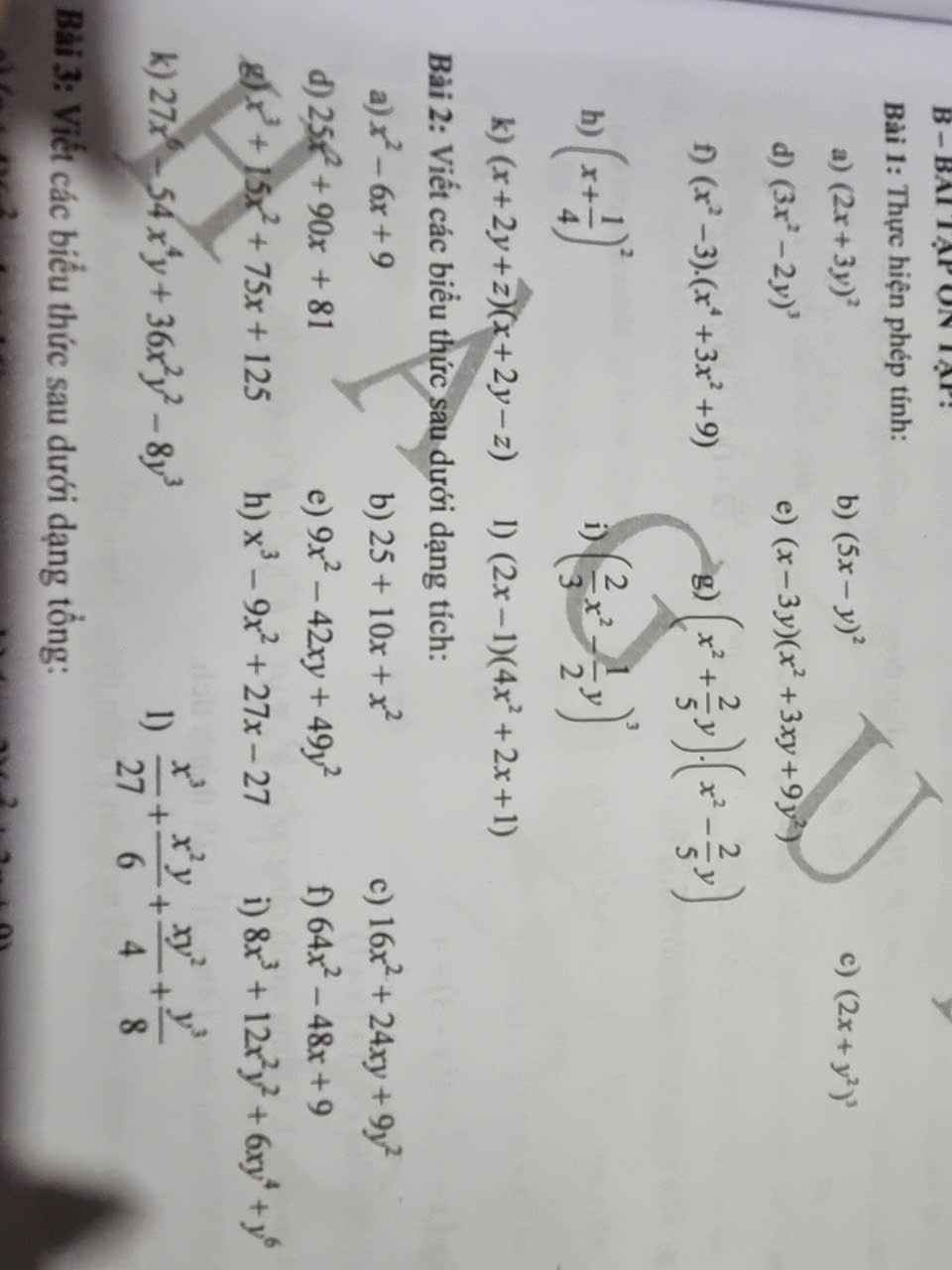
Bài 4: Những hằng đẳng thức đáng nhớ (Tiếp)
Bài 1:
a: \(\left(2x+3y\right)^2\)
\(=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2\)
\(=4x^2+12xy+9y^2\)
b: \(\left(5x-y\right)^2=\left(5x\right)^2-2\cdot5x\cdot y+y^2=25x^2-10xy+y^2\)
c: \(\left(2x+y^2\right)^3\)
\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y^2+3\cdot2x\cdot\left(y^2\right)^2+\left(y^2\right)^3\)
\(=8x^3+12x^2y^2+6xy^4+y^6\)
d: \(\left(3x^2-2y\right)^3\)
\(=\left(3x^2\right)^3-3\cdot\left(3x^2\right)^2\cdot2y+3\cdot3x^2\cdot\left(2y\right)^2-\left(2y\right)^3\)
\(=27x^6-54x^4y+36x^2y^2-8y^3\)
e: \(\left(x-3y\right)\left(x^2+3xy+9y^2\right)\)
\(=\left(x-3y\right)\left(x^2+x\cdot3y+\left(3y\right)^2\right)\)
\(=x^3-\left(3y\right)^3=x^3-27y^3\)
f: \(\left(x^2-3\right)\left(x^4+3x^2+9\right)\)
\(=\left(x^2-3\right)\left[\left(x^2\right)^2+x^2\cdot3+3^2\right]\)
\(=\left(x^2\right)^3-3^3=x^6-27\)
g: \(\left(x^2+\dfrac{2}{5}y\right)\left(x^2-\dfrac{2}{5}y\right)=\left(x^2\right)^2-\left(\dfrac{2}{5}y\right)^2=x^4-\dfrac{4}{25}y^2\)
h: \(\left(x+\dfrac{1}{4}\right)^2=x^2+2\cdot x\cdot\dfrac{1}{4}+\left(\dfrac{1}{4}\right)^2=x^2+\dfrac{1}{2}x+\dfrac{1}{16}\)
i: \(\left(\dfrac{2}{3}x^2-\dfrac{1}{2}y\right)^3\)
\(=\left(\dfrac{2}{3}x^2\right)^3-3\cdot\left(\dfrac{2}{3}x^2\right)^2\cdot\dfrac{1}{2}y+3\cdot\dfrac{2}{3}x^2\cdot\left(\dfrac{1}{2}y\right)^2-\left(\dfrac{1}{2}y\right)^3\)
\(=\dfrac{8}{27}x^6-\dfrac{2}{3}x^4y+\dfrac{1}{2}x^2y^2-\dfrac{1}{8}y^3\)
k: \(\left(x+2y+z\right)\left(x+2y-z\right)\)
\(=\left(x+2y\right)^2-z^2\)
\(=x^2+4xy+4y^2-z^2\)
l: \(\left(2x-1\right)\left(4x^2+2x+1\right)\)
\(=\left(2x-1\right)\left[\left(2x\right)^2+2x\cdot1+1^2\right]\)
\(=\left(2x\right)^3-1^3=8x^3-1\)
Bài 2:
a: \(x^2-6x+9=x^2-2\cdot x\cdot3+3^2=\left(x-3\right)^2\)
b: \(25+10x+x^2=5^2+2\cdot5\cdot x+x^2=\left(5+x\right)^2\)
c: \(16x^2+24xy+9y^2\)
\(=\left(4x\right)^2+2\cdot4x\cdot3y+\left(3y\right)^2\)
\(=\left(4x+3y\right)^2\)
d: \(25x^2+90x+81\)
\(=\left(5x\right)^2+2\cdot5x\cdot9+9^2\)
\(=\left(5x+9\right)^2\)
e: \(9x^2-42xy+49y^2\)
\(=\left(3x\right)^2-2\cdot3x\cdot7y+\left(7y\right)^2\)
\(=\left(3x-7y\right)^2\)
f: \(64x^2-48x+9\)
\(=\left(8x\right)^2-2\cdot8x\cdot3+3^2\)
\(=\left(8x-3\right)^2\)
g: \(x^3+15x^2+75x+125\)
\(=x^3+3\cdot x^2\cdot5+3\cdot x\cdot5^2+5^3\)
\(=\left(x+5\right)^3\)
h: \(x^3-9x^2+27x-27\)
\(=x^3-3\cdot x^2\cdot3+3\cdot x\cdot3^2-3^3\)
\(=\left(x-3\right)^3\)
i: \(8x^3+12x^2y^2+6xy^4+y^6\)
\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y^2+3\cdot2x\cdot\left(y^2\right)^2+\left(y^2\right)^3\)
\(=\left(2x+y^2\right)^3\)
k: \(27x^6-54x^4y+36x^2y^2-8y^3\)
\(=\left(3x^2\right)^3-3\cdot\left(3x^2\right)^2\cdot2y+3\cdot3x^2\cdot\left(2y\right)^2-\left(2y\right)^3\)
\(=\left(3x^2-2y\right)^3\)
l: \(\dfrac{x^3}{27}+\dfrac{x^2y}{6}+\dfrac{xy^2}{4}+\dfrac{y^3}{8}\)
\(=\left(\dfrac{1}{3}x\right)^3+3\cdot\left(\dfrac{1}{3}x\right)^2\cdot\dfrac{y}{2}+3\cdot\dfrac{1}{3}x\cdot\left(\dfrac{1}{2}y\right)^2+\left(\dfrac{1}{2}y\right)^3\)
\(=\left(\dfrac{1}{3}x+\dfrac{1}{2}y\right)^3\)
Đúng 0
Bình luận (0)
Bài 3:
\(M+4y-2xy^2+xy-9=4y-3\)
=>\(M=4y-3-4y+2xy^2-xy+9\)
=>\(M=2xy^2-xy+6\)
Bài 1:
Thay a=11;b=1 vào A, ta được:
\(A=a^2-2ab+b=11^2-2\cdot11\cdot1+1=\left(11-1\right)^2=10^2=100\)
Bài 4:
1: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{B}+110^0+80^0+50^0=360^0\)
=>\(\widehat{B}=360^0-190^0-50^0=120^0\)
2:
a: ta có: \(AE=EB=\dfrac{AB}{2}\)
\(DF=FC=\dfrac{DC}{2}\)
mà AB=DC(ABCD là hình bình hành)
nên AE=EB=DF=FC
=>AE=DF
b: Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>BF//DE
Đúng 2
Bình luận (0)
Bài `2:`
`a)8x^2y^3(-1/2xyz^2)`
`=8*(-1/2)*(x^2*x)*(y^3*y)*z`
`=-4x^3y^4z`
`b)[12x^2y+(-6x^2y^3)+5xy]:3xy`
`=(12x^2y:3xy)-(6x^2y^3:3xy)+(5xy:3xy)`
`=4x-2xy^2+5/3`
`c)2x^2(3x^2-7xy+3y)`
`=(2x^2*3x^2)-(2x^2*7xy)+(2x^2*3y)`
`=6x^4-14x^3y+6x^2y`
Đúng 1
Bình luận (0)
Bài 1:
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{C}+110^0+70^0+70^0=360^0\)
=>\(\widehat{C}=110^0\)
b: Xét tứ giác ABCD có
\(\widehat{A}=\widehat{C}\left(=110^0\right)\)
\(\widehat{B}=\widehat{D}\left(=70^0\right)\)
Do đó: ABCD là hình bình hành
c: ta có: ABCD là hình bình hành
=>AB//CD và AB=CD
AB//CD
=>AB//CE
Ta có: AB=CD
CD=CE
Do đó: AB=CE
Xét tứ giác ABEC có
AB//EC
AB=EC
Do đó: ABEC là hình bình hành
=>AC=BE
Bài 2:
a: Ta có: FM\(\perp\)AC
AB\(\perp\)AC
Do đó: FM//AB
=>\(\widehat{FMB}+\widehat{B}=180^0\)
=>\(\widehat{FMB}=180^0-59^0=121^0\)
b: Xét tứ giác AEMF có \(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
nên AEMF là hình chữ nhật
c: AEMF là hình chữ nhật
=>AM=EF
ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}\)
=>\(EF=\dfrac{1}{2}BC\)
Đúng 2
Bình luận (0)
Bài 1:
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{C}=360^0-70^0-70^0-110^0=110^0\)
b: Xét tứ giác ABCD có
\(\widehat{A}=\widehat{C}=110^0\)
\(\widehat{B}=\widehat{D}=70^0\)
Do đó: ABCD là hình bình hành
c: ABCD là hình bình hành
=>AB//CD và AB=CD
AB//CD
=>AB//CE
Ta có: AB=CD
CD=CE
Do đó: AB=CE
Xét tứ giác ABEC có
AB//EC
AB=EC
Do đó: ABEC là hình bình hành
=>AC=BE
Bài 2:
a: Ta có: MF\(\perp\)AC
AB\(\perp\)AC
Do đó: MF//AB
=>\(\widehat{BMF}+\widehat{MBA}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{BMF}=180^0-59^0=121^0\)
b: Xét tứ giác AEMF có \(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
nên AEMF là hình chữ nhật
c: AEMF là hình chữ nhật
=>ME//AF
=>ME//AC
ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}\)
mà AM=EF(AEMF là hình chữ nhật)
nên \(EF=\dfrac{1}{2}BC\)
Đúng 2
Bình luận (0)
Bài 1:
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{C}=360^0-70^0-70^0-110^0=110^0\)
b: Xét tứ giác ABCD có
\(\widehat{A}=\widehat{C}=110^0\)
\(\widehat{B}=\widehat{D}=70^0\)
Do đó: ABCD là hình bình hành
c: ABCD là hình bình hành
=>AB//CD và AB=CD
AB//CD
=>AB//CE
Ta có: AB=CD
CD=CE
Do đó: AB=CE
Xét tứ giác ABEC có
AB//EC
AB=EC
Do đó: ABEC là hình bình hành
=>AC=BE
Bài 2:
a: Ta có: MF\(\perp\)AC
AB\(\perp\)AC
Do đó: MF//AB
=>\(\widehat{BMF}+\widehat{MBA}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{BMF}=180^0-59^0=121^0\)
b: Xét tứ giác AEMF có \(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
nên AEMF là hình chữ nhật
c: AEMF là hình chữ nhật
=>ME//AF
=>ME//AC
ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}\)
mà AM=EF(AEMF là hình chữ nhật)
nên \(EF=\dfrac{1}{2}BC\)
Đúng 1
Bình luận (0)
a, (x+2)^3 b, (x+1)^3 c, (2x-1)^3 d, (xy+3)^3 e, (2x+3y)^3 f, (3x-y)^3 g, (1/3x-2)^3
h,(x^2+1/2y)^3
`(x+2)^3 = x^3 + 3x^2 . 2 + 3x . 2^2 + 2^3 = x^3 + 6x^2 + 12x + 8`
`(x+1)^3 = x^3 + 3x^2 . 1 + 3x.1^2 + 1^3 = x^3 + 3x^3 + 3x + 1`
`(2x - 1)^3 = (2x)^3 - 3.(2x)^2 . 1 + 3.2x . 1^2 - 1^3 = 8x^3 - 12x^2 + 6x - 1`
`(xy+3)^3 = (xy)^3 + 3.(xy)^2 . 3 + 3xy.3^2 + 3^3 = x^3 y^3 + 9x^2 y^2 + 27xy + 27`
Đúng 4
Bình luận (1)
`(3x - y)^3 = (3x)^3 - 3.(3x)^2 . y + 3.3x . y^2 - y^3 = 27x^3 - 27x^2 y + 9xy^2 - y^3`
`(1/3 x - 2)^3 = (1/3x)^3 - 3 .(1/3x)^2 .2 + 3 . (1/3x) . 2^2 - 2^3 = 1/27 x^3 - 2/3 x^2 + 4x - 8`
`(x^2 + 1/2y)^3 = (x^2)^3 + 3 . (x^2)^2 . 1/2y + 3 . x^2 . (1/2y)^2 + (1/2y)^3 `
`= x^6 + 3/2 x^4 y + 3/4 x^2 y^2 + 1/8 y^3`
Đúng 0
Bình luận (0)
a,x(x+1)(x+6)-x^3=5x b,(3x-5)(7-5x)+(5x+2)(3x-2)-2=0 c, 2(x-3)+7(2-x)+11
a: \(x\left(x+1\right)\left(x+6\right)-x^3=5x\)
=>\(x\cdot\left(x^2+7x+6\right)-x^3-5x=0\)
=>\(x^3+7x^2+6x-x^3-5x=0\)
=>\(7x^2+x=0\)
=>x(7x+1)=0
=>\(\left[{}\begin{matrix}x=0\\7x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{7}\end{matrix}\right.\)
b: \(\left(3x-5\right)\left(-5x+7\right)+\left(5x+2\right)\left(3x-2\right)-2=0\)
=>\(-15x^2+21x+25x-35+15x^2-10x+6x-4-2=0\)
=>42x-41=0
=>42x=41
=>\(x=\dfrac{41}{42}\)
Đúng 1
Bình luận (0)
(8x^3(2x-5)^2-6x^2(2x-5)^3+10x(2x-5)^2):2x(2x-5)^2
\(\dfrac{\left[8x^3\left(2x-5\right)^2-6x^2\left(2x-5\right)^3+10x\left(2x-5\right)^2\right]}{2x\left(2x-5\right)^2}\)
\(=\dfrac{8x^3\left(2x-5\right)^2}{2x\left(2x-5\right)^2}-\dfrac{6x^2\left(2x-5\right)^3}{2x\left(2x-5\right)^2}+\dfrac{10x\left(2x-5\right)^2}{2x\left(2x-5\right)^2}\)
\(=4x^2-3x\left(2x-5\right)+5\)
\(=4x^2-6x^2+15x+5=-2x^2+15x+5\)
Đúng 1
Bình luận (0)
a,x(x+1)(x+6)-x^3=5x b,(3x-5)(7-5x)+(5x+2)(3x-2)-2=0 c, 2(x-3)+7(2-x)+11
a: \(x\left(x+1\right)\left(x+6\right)-x^3=5x\)
=>\(x\cdot\left(x^2+7x+6\right)-x^3-5x=0\)
=>\(x^3+7x^2+6x-x^3-5x=0\)
=>\(7x^2+x=0\)
=>x(7x+1)=0
=>\(\left[{}\begin{matrix}x=0\\7x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{7}\end{matrix}\right.\)
b: \(\left(3x-5\right)\left(-5x+7\right)+\left(5x+2\right)\left(3x-2\right)-2=0\)
=>\(-15x^2+21x+25x-35+15x^2-10x+6x-4-2=0\)
=>42x-41=0
=>42x=41
=>\(x=\dfrac{41}{42}\)
Đúng 1
Bình luận (0)
a,x(x+1)(x+6)-x^3=5x b,(3x-5)(7-5x)+(5x+2)(3x-2)-2=0 c, 2(x-3)+7(2-x)+11
a) \(x\left(x+1\right)\left(x+6\right)-x^3=5x\)
\(\Leftrightarrow x\left(x^2+7x+6\right)-x^3=5x\)
\(\Leftrightarrow x^3+7x^2+6x-x^3-5x=0\)
\(\Leftrightarrow7x^2+x=0\)
\(\Leftrightarrow x\left(7x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{7}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c: Đề thiếu vế phải rồi bạn
a: \(x\left(x+1\right)\left(x+6\right)-x^3=5x\)
=>\(x\cdot\left(x^2+7x+6\right)-x^3-5x=0\)
=>\(x^3+7x^2+6x-x^3-5x=0\)
=>\(7x^2+x=0\)
=>x(7x+1)=0
=>\(\left[{}\begin{matrix}x=0\\7x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{7}\end{matrix}\right.\)
b: \(\left(3x-5\right)\left(-5x+7\right)+\left(5x+2\right)\left(3x-2\right)-2=0\)
=>\(-15x^2+21x+25x-35+15x^2-10x+6x-4-2=0\)
=>42x-41=0
=>42x=41
=>\(x=\dfrac{41}{42}\)
Đúng 0
Bình luận (0)







