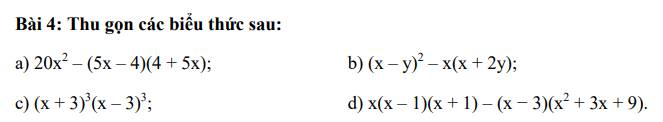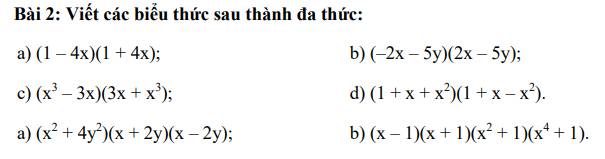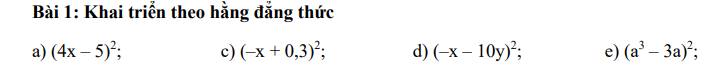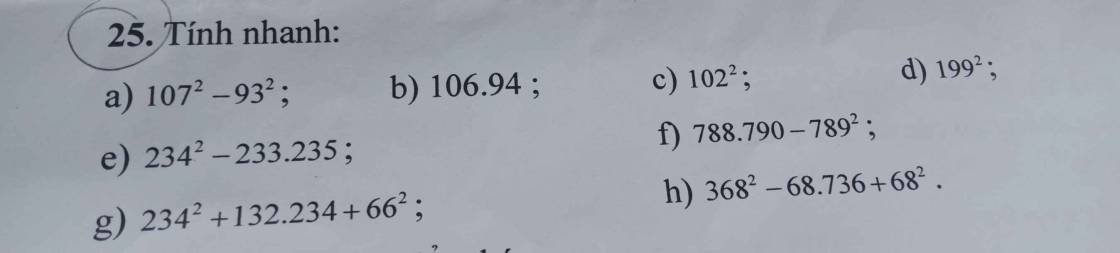Bài 3: Những hằng đẳng thức đáng nhớ

a)

\(P=(x-10)^2-x(x+80)\\=x^2-2\cdot x\cdot10+10^2-x^2-80x\\=x^2-20x+100-x^2-80x\\=-100x+100\\=-100(x-1)\)

Thay \(x=0,87\) vào \(P\), ta được:

\(P=-100(0,87-1)=-100\cdot(-0,13)=13\)

\(---\)

b)

\(Q=4a^2+8ab+4b^2\\=4(a^2+2ab+b^2)\\=4(a+b)^2\)

Thay \(a=65;b=35\) vào \(Q\), ta được:

\(Q=4(65+35)^2\\=4\cdot 100^2\\=4\cdot 10000\\=40000\)

\(---\)

c)

\(R=x^3-3x^2+3x-1\\=x^3-3\cdot x^2\cdot1+3\cdot x\cdot 1^2-1^3\\=(x-1)^3\)

Thay \(x=101\) vào \(R\), ta được:

\(R=(101-1)^3\\=100^3\\=1000000\)

\(Toru\)

a: \(P=\left(x-10\right)^2-x\left(x+80\right)\)

\(=x^2-20x+100-x^2-80x=-100x+100\)

Khi x=0,87 thì \(P=100-100\cdot0.87=100-87=13\)

c: \(R=x^3-3x^2+3x-1\)

\(=x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3=\left(x-1\right)^3\)

Khi x=101 thì \(R=\left(101-1\right)^3=100^3=1000000\)

b: \(Q=4a^2+8ab+4b^2\)

\(=4\left(a^2+2ab+b^2\right)\)

\(=4\left(a+b\right)^2\)

Khi a=65 và b=35 thì \(Q=4\left(35+65\right)^2=4\cdot100^2=40000\)

a)

\(20x^2-(5x-4)(4+5x)\\=20x^2-(5x-4)(5x+4)\\=20x^2-[(5x)^2-4^2]\\=20x^2-(25x^2-16)\\=20x^2-25x^2+16\\=-5x^2+16\)

b)

\((x-y)^2-x(x+2y)\\=x^2-2xy+y^2-x^2-2xy\\=-4xy+y^2\)

c)

\((x+3)^3(x-3)^3\\=[(x+3)(x-3)]^3\\=(x^2-3^2)^3\\=(x^2-9)^3\\=(x^2)^3-3\cdot (x^2)^2\cdot9+3\cdot x^2\cdot9^2-9^3\\=x^6-27x^4+243x^2-729\)

d)

\(x(x-1)(x+1)-(x-3)(x^2+3x+9)\\=x(x^2-1^2)-(x-3)(x^2+x\cdot3+3^2)\\=x^3-x-(x^3-3^3)\\=x^3-x-x^3+27\\=-x+27\\Toru\)

a: \(20x^2-\left(5x-4\right)\left(5x+4\right)\)

\(=20x^2-\left(25x^2-16\right)\)

\(=20x^2-25x^2+16=-5x^2+16\)

b: \(\left(x-y\right)^2-x\left(x+2y\right)\)

\(=x^2-2xy+y^2-x^2-2xy\)

\(=y^2-4xy\)

c: \(\left(x+3\right)^3\cdot\left(x-3\right)^3\)

\(=\left[\left(x+3\right)\left(x-3\right)\right]^3\)

\(=\left(x^2-9\right)^3\)

\(=x^6-27x^4+243x^2-729\)

d: \(x\left(x-1\right)\left(x+1\right)-\left(x-3\right)\left(x^2+3x+9\right)\)

\(=x\cdot\left(x^2-1\right)-\left(x^3-27\right)\)

\(=x^3-x-x^3+27=27-x\)

a: \(50.5^2-50.4^2=\left(50.5-50.4\right)\cdot\left(50.5+50.4\right)\)

\(=100.9\cdot0.1=10.09\)

b; \(202\cdot198=\left(200+2\right)\left(200-2\right)\)

\(=200^2-2^2=40000-4=39996\)

c: \(10.2^2=\left(10+0.2\right)^2\)

\(=10^2+2\cdot10\cdot0.2+0.2^2\)

\(=100+0.04+4=104.04\)

d: \(101^2-202\cdot71+71^2\)

\(=101^2-2\cdot101\cdot71+71^2\)

\(=\left(101-71\right)^2=50^2=2500\)

a: \(\left(1-4x\right)\left(1+4x\right)=1-\left(4x\right)^2=1-16x^2\)

b: \(\left(-2x-5y\right)\left(2x-5y\right)\)

\(=-\left(2x+5y\right)\left(2x-5y\right)\)

\(=-\left(4x^2-25y^2\right)=-4x^2+25y^2\)

c: \(\left(x^3-3x\right)\left(x^3+3x\right)=\left(x^3\right)^2-\left(3x\right)^2=x^6-9x^2\)

d: \(\left(1+x+x^2\right)\left(1+x-x^2\right)\)

\(=\left(1+x\right)^2-x^4=-x^4+x^2+2x+1\)

a: \(\left(x^2+4y^2\right)\left(x+2y\right)\left(x-2y\right)\)

\(=\left(x^2+4y^2\right)\left(x^2-4y^2\right)\)

\(=x^4-16y^4\)

b: \(\left(x-1\right)\left(x+1\right)\left(x^2+1\right)\left(x^4+1\right)\)

\(=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\)

\(=\left(x^4-1\right)\left(x^4+1\right)\)

\(=x^8-1\)

a) \(\left(4x-5\right)^2\)

\(=\left(4x\right)^2-2\cdot4x\cdot5+5^2\)

\(=16x^2-40x+25\)

b) \(\left(-x+0,3\right)^2\)

\(=\left(-x\right)^2+2\cdot\left(-x\right)\cdot0,3+\left(0,3\right)^2\)

\(=x^2-0,6x+0,09\)

c) \(\left(-x-10y\right)^2\)

\(=\left(-x\right)^2+2\cdot\left(-x\right)\cdot\left(-10y\right)+\left(-10y\right)^2\)

\(=x+20xy+100y^2\)

d) \(\left(a^3-3a\right)^2\)

\(=\left(a^3\right)^2-2\cdot a^3\cdot3a+\left(3a\right)^2\)

\(=a^6-6a^4+9a^2\)

a: \(\left(4x-5\right)^2=\left(4x\right)^2-2\cdot4x\cdot5+5^2=16x^2-40x+25\)

c: \(\left(-x+0.3\right)^2=\left(-x\right)^2+2\cdot\left(-x\right)\cdot0.3+0.3^2\)

\(=x^2-0.6x+0.09\)

d: \(\left(-x-10y\right)^2=\left(x+10y\right)^2\)

\(=x^2+2\cdot x\cdot10y+\left(10y\right)^2\)

\(=x^2+20xy+100y^2\)

e: \(\left(a^3-3a\right)^2\)

\(=\left(a^3\right)^2-2\cdot a^3\cdot3a+\left(3a\right)^2\)

\(=a^6-6a^4+9a^2\)

`(x+y)^2 -2(x+y)(x-y)+(x-y)^2`

\(=\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =\left(2y\right)^2\\ =4y^2\)

a) \(107^2-93^2\)

\(=\left(107-93\right)\left(107+93\right)\)

\(=14\cdot200\)

\(=2800\)

b) \(106\cdot94\)

\(=\left(100+6\right)\left(100-6\right)\)

\(=100^2-6^2\)

\(=10000-36\)

\(=9964\)

c) \(102^2\)

\(=\left(100+2\right)^2\)

\(=100^2+2\cdot100\cdot2+2^2\)

\(=10000+400+4\)

\(=10404\)

d) \(199^2\)

\(=\left(200-1\right)^2\)

\(=200^2-2\cdot200\cdot1+1^2\)

\(=40000-400+1\)

\(=39601\)

e) \(234^2-233\cdot235\)

\(=234^2-\left(234-1\right)\left(234+1\right)\)

\(=234^2-\left(234^2-1\right)\)

\(=234^2-234^2+1\)

\(=1\)

f) \(788\cdot790-789^2\)

\(=\left(789-1\right)\left(789+1\right)-789^2\)

\(=\left(789^2-1\right)-789^2\)

\(=789^2-1-789^2\)

\(=-1\)

g) \(234^2+132\cdot234+66^2\)

\(=234^2+2\cdot66\cdot234+66^2\)

\(=\left(234+66\right)^2\)

\(=300^2\)

\(=90000\)

h) \(368^2-68\cdot736+68^2\)

\(=368^2-2\cdot368\cdot68+68^2\)

\(=\left(368-68\right)^2\)

\(=300^2\)

\(=90000\)

\(f,F=x^2+9y^2-8x+4y+27\) (sửa đề)

\(=\left(x^2-8x+16\right)+\left(9y^2+4y+\dfrac{4}{9}\right)+\dfrac{95}{9}\)

\(=\left(x^2-2\cdot x\cdot4+4^2\right)+\left[\left(3y\right)^2+2\cdot3y\cdot\dfrac{2}{3}+\left(\dfrac{2}{3}\right)^2\right]+\dfrac{95}{9}\)

\(=\left(x-4\right)^2+\left(3y+\dfrac{2}{3}\right)^2+\dfrac{95}{9}\)

Ta thấy: \(\left(x-4\right)^2\ge0\forall x\)

             \(\left(3y+\dfrac{2}{3}\right)^2\ge0\forall y\)

\(\Rightarrow\left(x-4\right)^2+\left(3y+\dfrac{2}{3}\right)^2\ge0\forall x;y\)

\(\Rightarrow\left(x-4\right)^2+\left(3y+\dfrac{2}{3}\right)^2+\dfrac{95}{9}\ge\dfrac{95}{9}>0\forall x;y\)

hay \(F\) luôn dương với mọi \(x;y\).

\(Toru\)

Viết liền thế ai mà đọc được

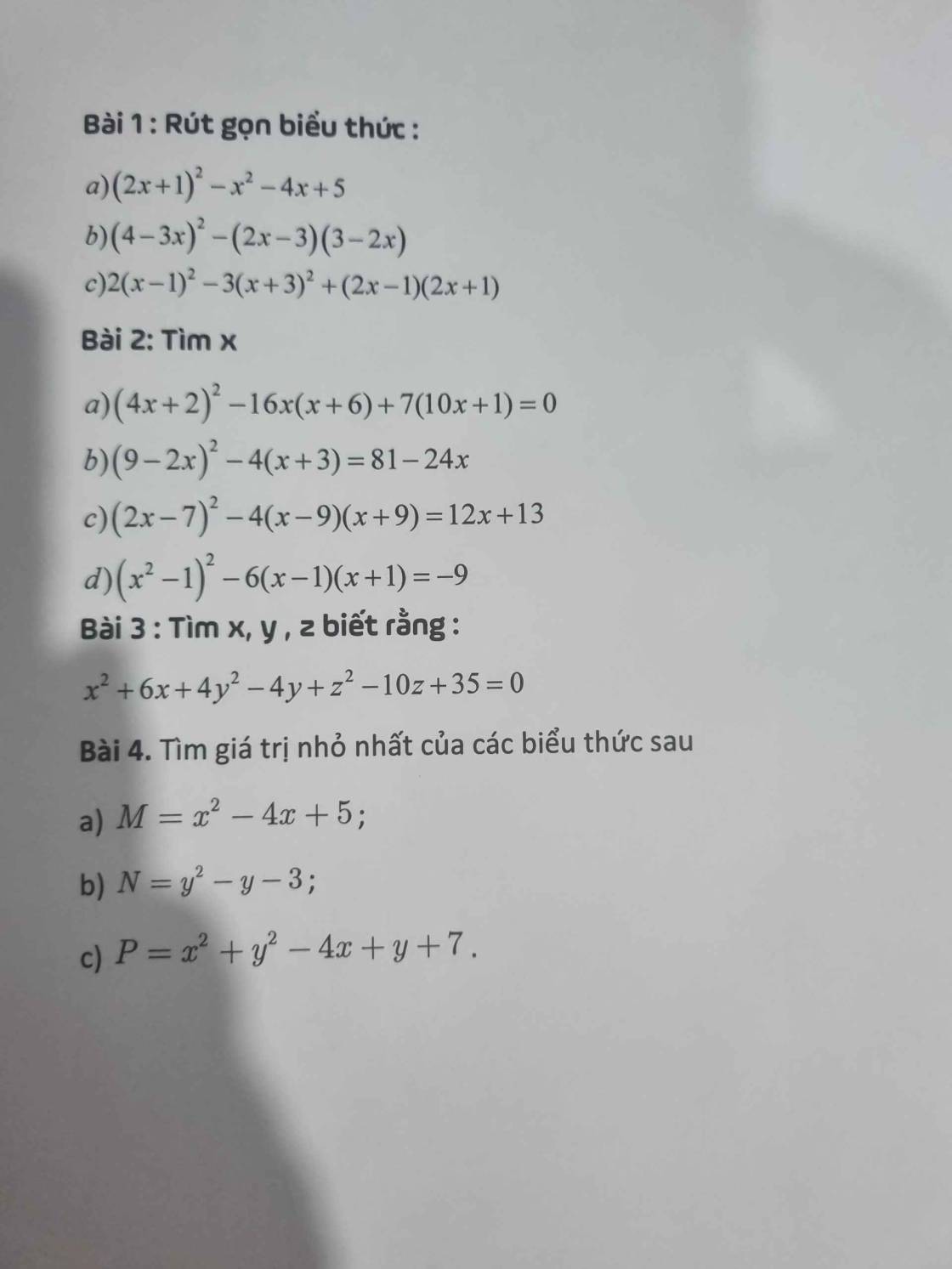
1:

a: \(=4x^2+4x+1-x^2-4x+5\)

\(=3x^2+6\)

b: \(=9x^2-24x+16+\left(2x-3\right)^2\)

\(=9x^2-24x+16+4x^2-12x+9\)

\(=13x^2-36x+25\)

c: \(=2\left(x^2-2x+1\right)-3\left(x^2+6x+9\right)+4x^2-1\)

\(=2x^2-4x+2-3x^2-18x-27+4x^2-1\)

\(=3x^2-22x-26\)