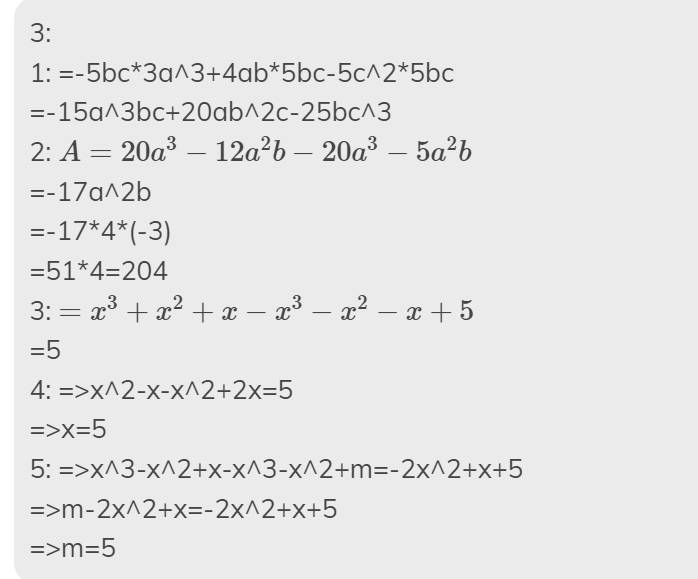Anh nguyễn le phước thịnh lấy -4x^2 ở đâu ạ e chx hiểu 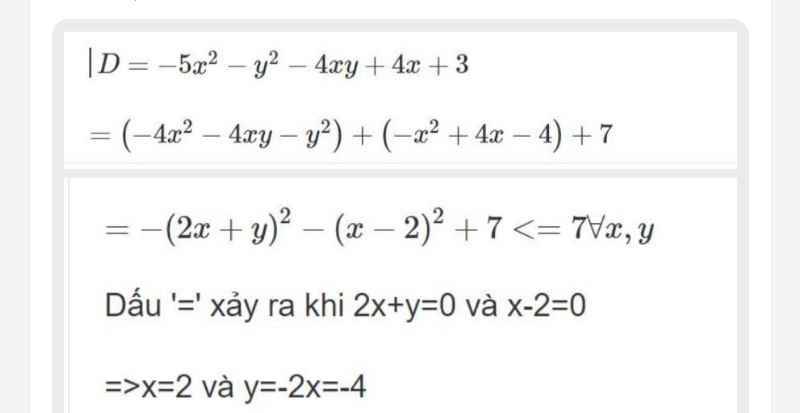
Bài 1: Nhân đơn thức với đa thức
tách -5x2 ra thôi bạn ơi
Đúng 2
Bình luận (0)
Tìm max -4xy+4x-y^2-5x^2+3
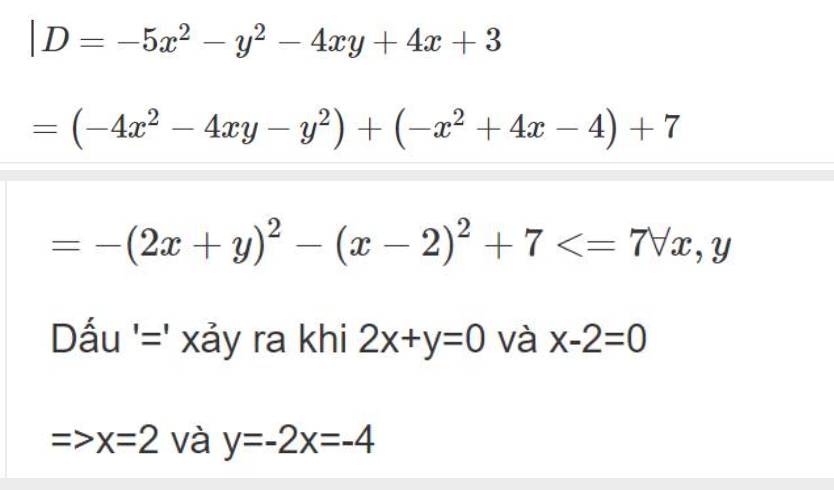
Vậy: \(D_{max}=7\) khi x=2 và y=-4
Đúng 0
Bình luận (0)
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
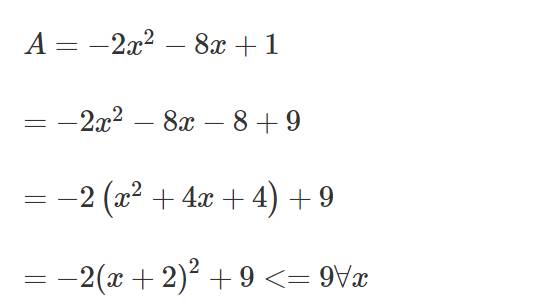
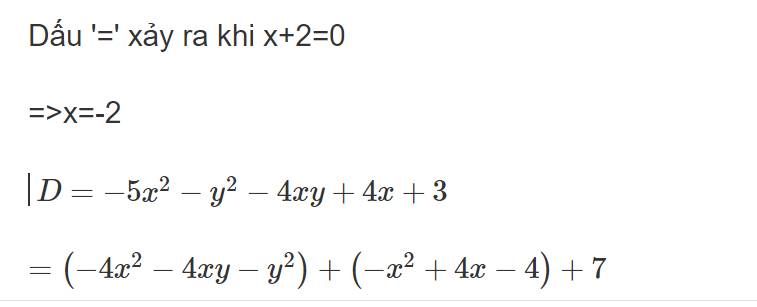
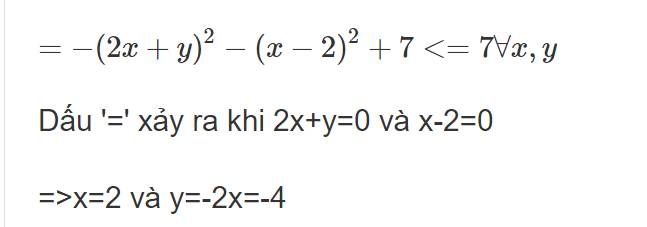
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất -2x^2-8x+1
-4xy+4x-y^2-5x^2+3 giúp chi tiết
a: \(-2x^2-8x+1\)
\(=-2x^2-8x-8+9\)
\(=-2\left(x^2+4x+4\right)+9\)
\(=-2\left(x+2\right)^2+9< =9\forall x\)
Dấu '=' xảy ra khi x+2=0
=>x=-2
b: \(-5x^2-y^2-4xy+4x+3\)
\(=\left(-4x^2-4xy-y^2\right)+\left(-x^2+4x-4\right)+7\)
\(=-\left(2x+y\right)^2-\left(x-2\right)^2+7< =7\forall x,y\)
Dấu '=' xảy ra khi 2x+y=0 và x-2=0
=>x=2 và y=-2x=-4
Đúng 0
Bình luận (0)
Cho tứ giác ABCD gọi K và I lần lượt là trung điểm của AB và CD
a)Chứng minh AI=CK và góc IAC = góc KCA
b) Chứng minh AI song song với CK
a: Sửa đề; ABCD là hình bình hành
ABCD là hình bình hành
=>AB=CD(1)
K là trung điểm của AB
=>\(KA=KB=\dfrac{AB}{2}\left(2\right)\)
I là trung điểm của CD
=>\(IC=ID=\dfrac{CD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra KA=KB=IC=ID
Xét ΔADI và ΔCBK có
AD=CB
\(\widehat{ADI}=\widehat{CBK}\)(ABCD là hình bình hành)
DI=BK
Do đó: ΔADI=ΔCBK
=>AI=CK và \(\widehat{DAI}=\widehat{BCK}\)
Xét ΔDAC và ΔBCA có
DA=BC
AC chung
DC=BA
Do đó: ΔDAC=ΔBCA
=>\(\widehat{DAC}=\widehat{BCA}\)
Ta có: \(\widehat{DAI}+\widehat{IAC}=\widehat{DAC}\)
\(\widehat{BCK}+\widehat{KCA}=\widehat{BCA}\)
mà \(\widehat{DAI}=\widehat{BCK};\widehat{DAC}=\widehat{BCA}\)
nên \(\widehat{IAC}=\widehat{KCA}\)
b: ta có: \(\widehat{IAC}=\widehat{KCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AI//CK
Đúng 1
Bình luận (0)
Rút gọn cái biểu thức sau r tính giá trị biểu thức F=-(2x-y) ^3-x(2x-y)^2-y^3 tại (x-2)^2 +y^2=0 G=(x+y) (x^2-xy+y^2) +3(2x-y) (4x^2+2xy+y^2) tại x+y=2;y=-3 H=(X+3y) (x^2-3xy+9y^2) +(3x-y) (9x^2+3xy+y^2) tại 3x-y=5;x=2
a: \(F=-\left(2x-y\right)^3-x\left(2x-y\right)^2-y^3\)
\(=-\left(2x-y\right)^2\cdot\left[2x-y+x\right]-y^3\)
\(=-\left(2x-y\right)^2\cdot\left(3x-y\right)-y^3\)
\(=\left(-4x^2+4xy-y^2\right)\left(3x-y\right)-y^3\)
\(=-12x^3+4x^2y+12x^2y-4xy^2-3xy^2+y^3-y^3\)
\(=-12x^3+16x^2y-7xy^2\)
\(\left(x-2\right)^2+y^2=0\)
mà \(\left(x-2\right)^2+y^2>=0\forall x,y\)
nên dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2=0\\y=0\end{matrix}\right.\)
=>x=2 và y=0
Thay x=2 và y=0 vào F, ta được:
\(F=-12\cdot2^3+16\cdot2^2\cdot0-7\cdot2\cdot0^2\)
\(=-12\cdot2^3\)
\(=-12\cdot8=-96\)
b: \(G=\left(x+y\right)\left(x^2-xy+y^2\right)+3\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(=x^3+y^3+3\left(2x-y\right)\left[\left(2x\right)^2+2x\cdot y+y^2\right]\)
\(=x^3+y^3+3\left(8x^3-y^3\right)\)
\(=x^3+y^3+24x^3-3y^3\)
\(=25x^3-2y^3\)
Ta có: \(\left\{{}\begin{matrix}x+y=2\\y=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-3\\x=2-y=2-\left(-3\right)=2+3=5\end{matrix}\right.\)
Thay x=5 và y=-3 vào G, ta được:
\(G=25\cdot5^3-2\cdot\left(-3\right)^3\)
\(=25\cdot125-2\cdot\left(-27\right)\)
\(=3125+54=3179\)
c: \(H=\left(x+3y\right)\left(x^2-3xy+9y^2\right)+\left(3x-y\right)\left(9x^2+3xy+y^2\right)\)
\(=\left(x+3y\right)\left[x^2-x\cdot3y+\left(3y\right)^2\right]+\left(3x-y\right)\left[\left(3x\right)^2+3x\cdot y+y^2\right]\)
\(=x^3+27y^3+27x^3-y^3\)
\(=28x^3-26y^3\)
Ta có: \(\left\{{}\begin{matrix}3x-y=5\\x=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=3x-5=3\cdot2-5=1\end{matrix}\right.\)
Thay x=2 và y=1 vào H, ta được:
\(H=28\cdot2^3-26\cdot1^3\)
\(=28\cdot8-26\)
=198
Đúng 1
Bình luận (0)
x^2+8y^2+4xy+8y-4x+20=0
Bài 3:
1) \(\left(3a^3-4ab+5c^2\right)\left(-5bc\right)\)
\(=\left(3a^3\cdot-5bc\right)+\left(-4ab\cdot-5bc\right)+\left(5c^2\cdot-5bc\right)\)
\(=-15a^3bc+20ab^2c-25bc^3\)
2) \(A=4a^2\left(5a-3b\right)-5a^2\left(4a+b\right)\)
\(A=20a^3-12a^2b-20a^3-5a^2b\)
\(A=-19a^2b\)
Thay a=-2, b=-3 vào A ta có:
\(-19\cdot\left(-2\right)^2\cdot\left(-3\right)=228\)
3) \(B=x\left(x^2+x+1\right)-x^2\left(x+1\right)-x+5\)
\(B=x^3+x^2+x-x^3-x^2-x+5\)
\(=5\)
Vậy giá trị của biểu thức không phụ thuộc vào biến
4) \(x\left(x-1\right)-x^2+2x=5\)
\(\Leftrightarrow x^2-x-x^2+2x=5\)
\(\Leftrightarrow x=5\)
5) \(\left(x^2-x+1\right)x-\left(x+1\right)x^2+m=-2x^2+x+5\)
\(\Leftrightarrow x^3-x^2+x-x^3-x^2+m=-2x^2+x+5\)
\(\Leftrightarrow-2x^2+x+m=-2x^2+x+5\)
\(\Leftrightarrow-2x^2+2x^2+x-x+m=5\)
\(\Leftrightarrow m=5\)
Đúng 1
Bình luận (0)
3:
1: =-5bc*3a^3+4ab*5bc-5c^2*5bc
=-15a^3bc+20ab^2c-25bc^3
2: \(A=20a^3-12a^2b-20a^3-5a^2b\)
=-17a^2b
=-17*4*(-3)
=51*4=204
3: \(=x^3+x^2+x-x^3-x^2-x+5\)
=5
4: =>x^2-x-x^2+2x=5
=>x=5
5: =>x^3-x^2+x-x^3-x^2+m=-2x^2+x+5
=>m-2x^2+x=-2x^2+x+5
=>m=5
Đúng 0
Bình luận (0)