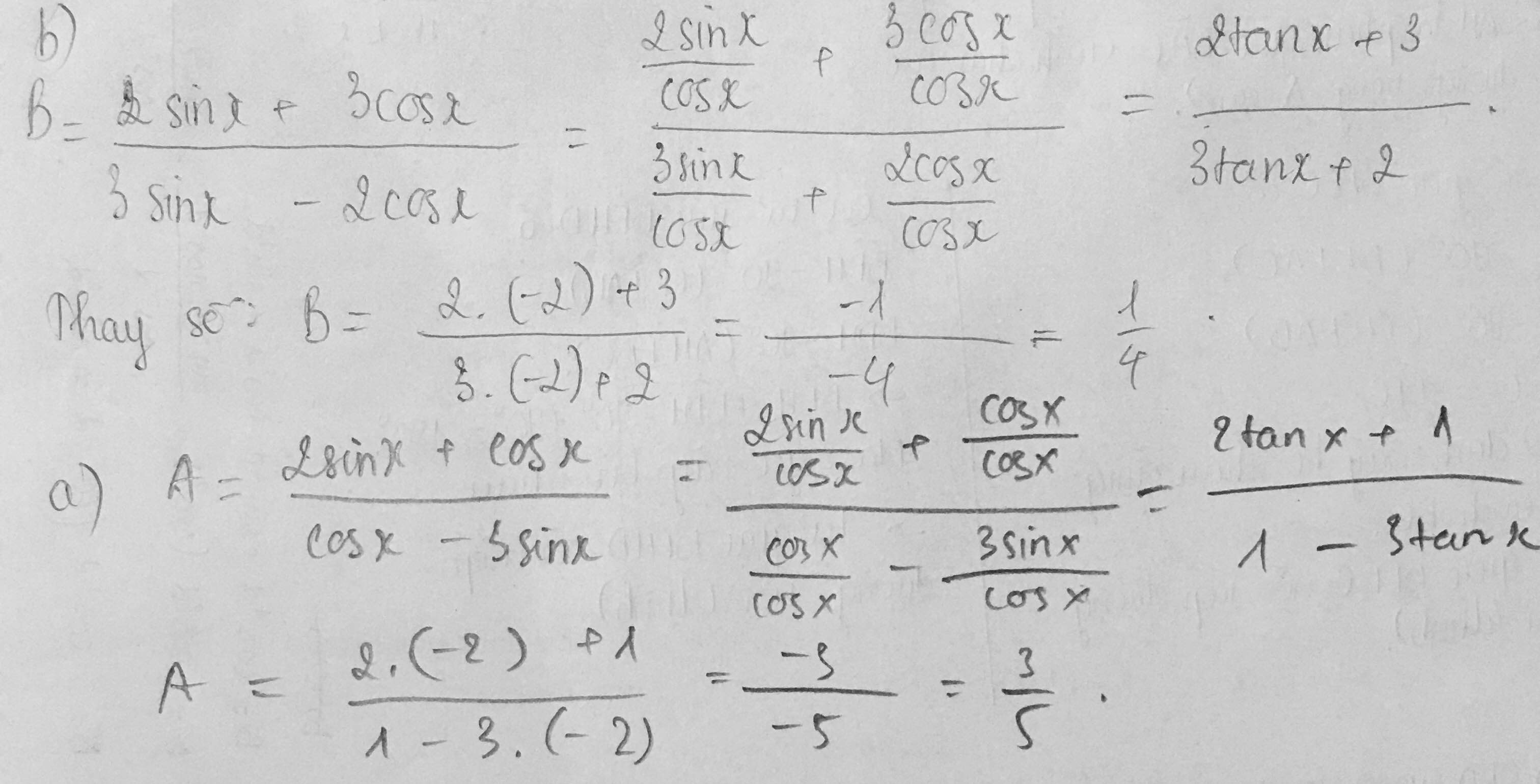Đề bài yêu cầu gì hả bạn ? 

a/ \(cosa=-\sqrt{1-sin^2a}=-\frac{\sqrt{5}}{3}\)

\(tana=\frac{sina}{cosa}=-\frac{2\sqrt{5}}{5}\) ; \(cota=\frac{1}{tana}=-\frac{\sqrt{5}}{2}\)

b/ \(\frac{1}{cos^2a}=1+tan^2a\Rightarrow cos^2a=\frac{1}{1+tan^2a}\)

\(\Rightarrow cosa=-\frac{1}{\sqrt{1+tan^2a}}=-\frac{\sqrt{3}}{3}\); \(sina=-\sqrt{1-cos^2a}=-\frac{\sqrt{6}}{3}\)

\(cota=\frac{1}{tana}=\frac{\sqrt{2}}{2}\)

c/ \(sina=\sqrt{1-cos^2a}=\frac{\sqrt{5}}{5}\); \(tana=\frac{sina}{cosa}=\frac{1}{2}\); \(cota=\frac{1}{tana}=2\)

d/ \(sina=\sqrt{1-cos^2a}=\frac{\sqrt{209}}{15}\); \(tana=\frac{sina}{cosa}=\frac{\sqrt{209}}{4}\); \(cota=\frac{1}{tana}=\frac{4}{\sqrt{209}}\)

e/ \(\frac{1}{sin^2a}=1+cot^2a\Rightarrow sin^2a=\frac{1}{1+cot^2a}\Rightarrow sina=\frac{-1}{\sqrt{1+cot^2a}}\)

\(\Rightarrow sina=-\frac{\sqrt{10}}{10}\); \(cosa=\sqrt{1-sin^2a}=\frac{3\sqrt{10}}{10}\); \(cota=\frac{1}{tana}=-\frac{1}{3}\)

f/ \(cosa=-\frac{1}{\sqrt{1+tan^2a}}=-\frac{\sqrt{5}}{5}\); \(sina=tana.cosa=\frac{2\sqrt{5}}{5}\); \(cota=\frac{1}{tana}=-\frac{1}{2}\)

g/ Đề sai, trong khoảng \(\pi< a< \frac{3\pi}{2}\) thì \(\left\{{}\begin{matrix}sina< 0\\cosa< 0\end{matrix}\right.\) nên \(tana>0\)

\(\Rightarrow tana\) không thể nhận giá trị âm, ko có góc \(\alpha\)

\(VT=\dfrac{-tan\left(\dfrac{\pi}{2}-a\right)cos\left(2\pi-\dfrac{\pi}{2}+a\right)-sin^3\left(4\pi-\dfrac{\pi}{2}-a\right)}{cos\left(\dfrac{\pi}{2}-a\right)tan\left(2\pi-\dfrac{\pi}{2}+a\right)}\)

\(=\dfrac{-cota.sina+sin^3\left(\dfrac{\pi}{2}+a\right)}{sina.\left(-cota\right)}=\dfrac{-cosa+cos^3a}{-cosa}=1-cos^2a=sin^2a\)

\(0< a< \frac{\pi}{2}\Rightarrow\left\{{}\begin{matrix}sina>0\\cosa>0\end{matrix}\right.\)

\(1+tan^2a=\frac{1}{cos^2a}\Rightarrow cos^2a=\frac{1}{1+tan^2a}\Rightarrow cosa=\frac{1}{\sqrt{1+tan^2a}}\)

\(\Rightarrow cosa=\frac{1}{2}\Rightarrow sina=cosa.tana=\frac{\sqrt{3}}{2}\)

\(cos2a=2cos^2a-1=-\frac{1}{2}\)

\(sin2a=2sina.cosa=\frac{\sqrt{3}}{2}\)

\(\Rightarrow sin\left(2a-\frac{\pi}{3}\right)=sin2a.cos\frac{\pi}{3}-cos2a.sin\frac{\pi}{3}=\frac{\sqrt{3}}{2}\)

\(tan\left(a+\frac{\pi}{4}\right)=\frac{tana+tan\frac{\pi}{4}}{1-tana.tan\frac{\pi}{4}}=-2-\sqrt{3}\)

a:

2: pi/2<a<pi

=>sin a>0 và cosa<0

tan a=-2

1+tan^2a=1/cos^2a=1+4=5

=>cos^2a=1/5

=>\(cosa=-\dfrac{1}{\sqrt{5}}\)

\(sina=\sqrt{1-\dfrac{1}{5}}=\dfrac{2}{\sqrt{5}}\)

cot a=1/tan a=-1/2

3: pi<a<3/2pi

=>cosa<0; sin a<0

1+cot^2a=1/sin^2a

=>1/sin^2a=1+9=10

=>sin^2a=1/10

=>\(sina=-\dfrac{1}{\sqrt{10}}\)

\(cosa=-\dfrac{3}{\sqrt{10}}\)

tan a=1:cota=1/3

b;

tan x=-2

=>sin x=-2*cosx

\(A=\dfrac{2\cdot sinx+cosx}{cosx-3sinx}\)

\(=\dfrac{-4cosx+cosx}{cosx+6cosx}=\dfrac{-3}{7}\)

2: tan x=-2 

=>sin x=-2*cosx

\(B=\dfrac{-4cosx+3cosx}{-6cosx-2cosx}=\dfrac{1}{8}\)

Do \(\alpha\in\left(\frac{\pi}{2};\frac{3\pi}{4}\right)\Rightarrow sin\alpha>0;cos\alpha< 0;tan\alpha< 0\)

\(\frac{tana}{cota}=\frac{\sqrt{5}-1}{\sqrt{5}+1}\Leftrightarrow tan^2a=\frac{\sqrt{5}-1}{\sqrt{5}+1}=\frac{\left(\sqrt{5}-1\right)^2}{4}\Rightarrow tana=\frac{1-\sqrt{5}}{2}\Rightarrow cota=\frac{-1-\sqrt{5}}{2}\)

\(1+tan^2a=\frac{1}{cos^2a}\Rightarrow cos^2a=\frac{1}{1+tan^2a}=\frac{5+\sqrt{5}}{10}\)

\(\Rightarrow sin^2a=1-cos^2a=\frac{5-\sqrt{5}}{10}\)

\(sin2a=2sina.cosa=2tana.cos^2a=-\frac{2\sqrt{5}}{5}\)

Thay vào ta được:

\(P=...\)

Bạn tự thay số và bấm máy

Lời giải:

$\frac{\pi}{2}< a< \pi$ nên $\sin a>0; \cos a< 0$

$-3=\tan a=\frac{\sin a}{\cos a}\Rightarrow \sin a=-3\cos a$

$\Rightarrow \sin ^2a=9\cos ^2a$

$\Rightarrow 10\sin ^2a=9(\sin ^2a+\cos ^2a)=9$

$\Rightarrow \sin ^2a=\frac{9}{10}$

$\Rightarrow \sin a=\frac{3}{\sqrt{10}}$

$\cos a=\frac{\sin a}{-3}=\frac{-1}{\sqrt{10}}$

$\cot a=\frac{1}{\tan a}=\frac{-1}{3}$