cho tam giác ABC có A=60 độ, B=36 độ, cạnh AB=2. Tính AC + BC \(\approx\)
§1. Cung và góc lượng giác
Áp dụng t/c tổng 3 góc trong 1 tam giác
=> \(\widehat{C}=180-60-36=84\)
Áp dụng định lí sin:
\(\dfrac{AB}{sin84}=\dfrac{BC}{sin60}=\dfrac{AC}{sin36}\)
\(\Rightarrow\left\{{}\begin{matrix}BC=\dfrac{sin60.AB}{sin84}\\AC=\dfrac{sin36.AB}{sin84}\end{matrix}\right.\)
\(AC+BC=\dfrac{AB\left(sin60+sin36\right)}{sin84}=\dfrac{2\left(sin60+sin36\right)}{sin84}\simeq2,9\)
Đúng 0
Bình luận (0)
Biết sin a=\(\dfrac{5}{13}\);cos b=\(\dfrac{3}{5}\); \(\dfrac{\text{π}}{2}\)<a<π; 0<b<\(\dfrac{\text{π}}{2}\). Hãy tính sin(a+b)
\(\cos a=\dfrac{-12}{13}\)
\(\sin b=\dfrac{4}{5}\)
\(\sin\left(a+b\right)=\sin a\cos b+\sin b\cos a\)
\(=\dfrac{5}{13}\cdot\dfrac{3}{5}+\dfrac{4}{5}\cdot\dfrac{-12}{13}=\dfrac{-45}{65}=\dfrac{-9}{13}\)
Đúng 1
Bình luận (0)
tính B=\(\sin\left(\dfrac{\pi}{4}+x\right)-\cos\left(\dfrac{\pi}{4}\right)-x\)
B=sin(pi/4)*cosx+sin(x)*cospi/4-cospi/4-x
=1/căn2(cosx+sinx)-1/căn 2-x
Đúng 0
Bình luận (0)
Rút gọn biểu thức :
P= \(\dfrac{cos\left(\dfrac{\pi}{2}-2x\right)+sinx}{sinx+sin2x+sin3x}\)
\(P=\dfrac{sin2x+sinx}{\dfrac{1}{2}\cdot cosx\cdot sin2x+sin2x}=\dfrac{sinx\left(2cosx+1\right)}{sin2x\left(\dfrac{1}{2}cosx+1\right)}\)
\(=\dfrac{2cosx+1}{2\cdot cosx\cdot\left(\dfrac{1}{2}cosx+1\right)}\)
Đúng 0
Bình luận (0)
Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay quay được góc 270 độ?
Sao lại ra chỗ k2pi /6 v ạ, gthich giúp e vs ạ, e cảm ơn ạ 
Cái này bạn quy đồng lên thôi
\(\dfrac{pi}{3}+\dfrac{kpi}{3}=\dfrac{2pi}{6}+\dfrac{k2pi}{6}=\dfrac{k2pi+2pi}{6}=\dfrac{\left(k+1\right)\cdot2pi}{6}\)
Do là k2pi và (k+1)2pi là hai điểm trùng nhau nên được tính chung luôn là k2pi bạn nha
Đúng 0
Bình luận (0)
Giải chi tiết mấy câu này giúp mình với ạ ( ét o ét cíuuuu ;-;)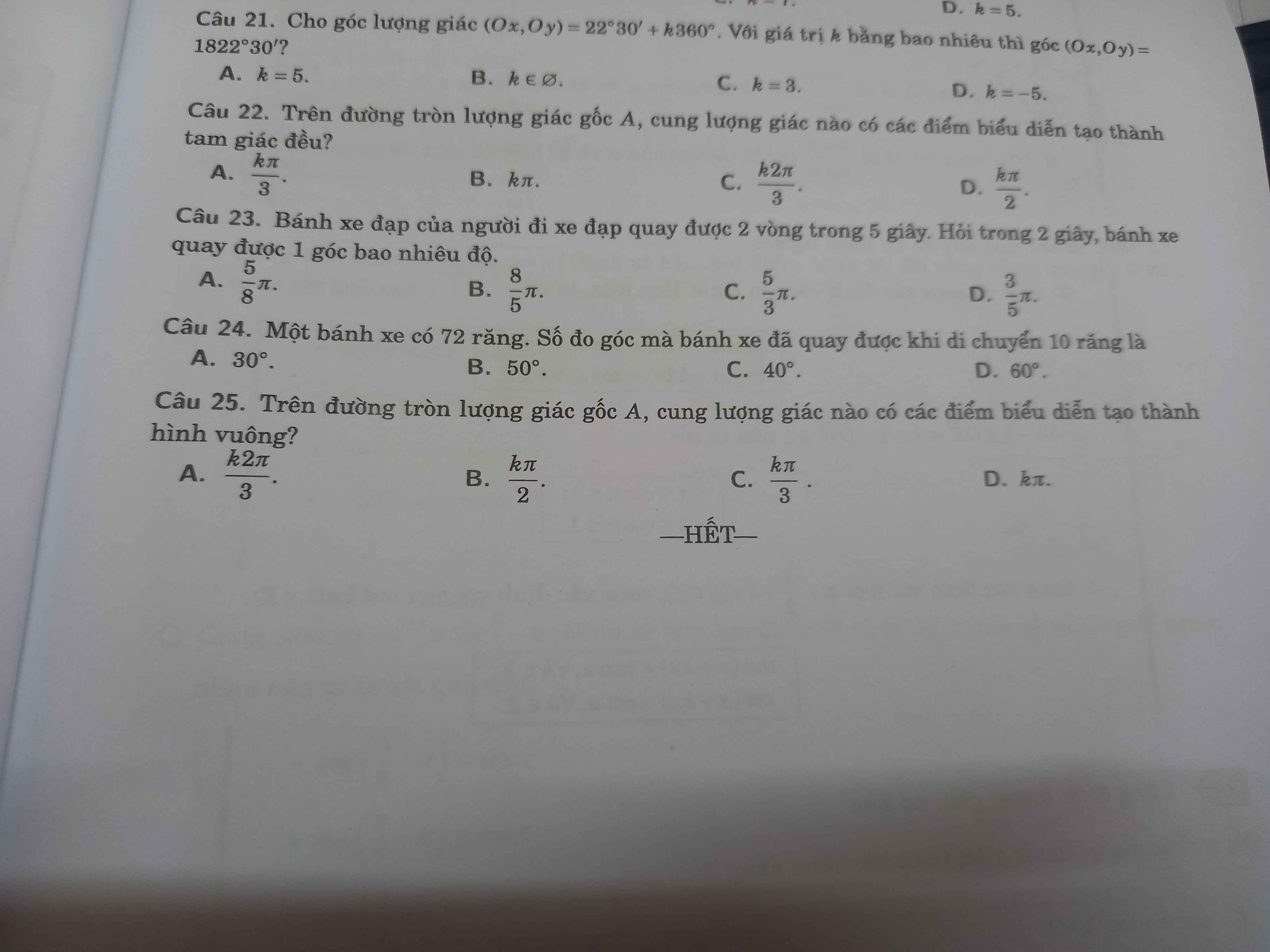
Giải chi tiết mấy câu này giúp mình với ạ ( ét o ét cíuuuu ;-;)
Câu 9: A
Câu 10: C
Câu 11: C
Câu 12: A
Câu 13; B
Câu 14: C
Đúng 2
Bình luận (0)
Giải chi tiết mấy câu này giúp mình với ạ ( ét o ét cíuuuu ;-;)
Câu 8: A
Câu 7: B
Câu 6: B
Câu 5: A
Đúng 1
Bình luận (0)
1/x-1+1/x+2>1/x-2 giúp tớ




