Cho hình vuông ABCD cạnh a.Tính các tích vô hướng sau: a)AB.AD;AB.BD b)(AB+AD).(BD+BC)
H24
Những câu hỏi liên quan
Cho hình vuông ABCD cạnh a túng các tích vô hướng a. Vectơ AB.AC b. vectơ AC.BD
a: ABCD là hình vuông
=>AC là phân giác của góc BAD và \(AC^2=AB^2+BC^2\)
AC là phân giác của góc BAD
=>\(\widehat{BAC}=\widehat{DAC}=\dfrac{1}{2}\cdot90^0=45^0\)
\(AC^2=AB^2+BC^2\)
=>\(AC^2=a^2+a^2=2a^2\)
=>\(AC=a\sqrt{2}\)
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB};\overrightarrow{AC}\right)\)
\(=a\cdot a\sqrt{2}\cdot cosBAC\)
\(=a^2\cdot\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=a^2\)
b: Vì ABCD là hình vuông
nên AC\(\perp\)BD
=>\(\overrightarrow{AC}\cdot\overrightarrow{BD}=0\)
Đúng 2
Bình luận (0)
Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau:
a) \(\overrightarrow {AB} .\overrightarrow {AC} \)
b) \(\overrightarrow {AC} .\overrightarrow {BD} \)
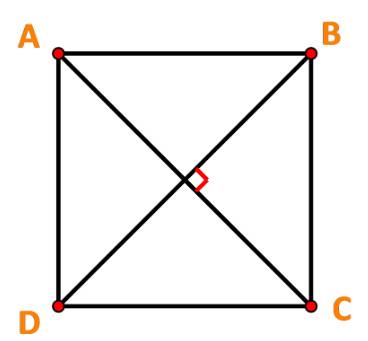
a) Ta có: \(AC = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2}} = a\sqrt 2 \)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = a.a\sqrt 2 .\cos \widehat {BAC} = {a^2}\sqrt 2 \cos {45^o} = {a^2}.\)
b) Dễ thấy: \(AC \bot BD \Rightarrow (\overrightarrow {AC} ,\overrightarrow {BD} ) = {90^o}\)
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = AC.BD.\cos {90^o} = AC.BD.0 = 0.\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a.Tính tích vô hướng \(\overrightarrow{SA.}\overrightarrow{CD}\) ?
\(\overrightarrow{SA}.\overrightarrow{CD}=\overrightarrow{SA}.\overrightarrow{BA}=\overrightarrow{AS}.\overrightarrow{AB}=a.a.cos60^0=\dfrac{a^2}{2}\)
Đúng 2
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng:
\(\overrightarrow {AB} .\overrightarrow {AD} ,\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {CB} ,\overrightarrow {AC} .\overrightarrow {BD} \)
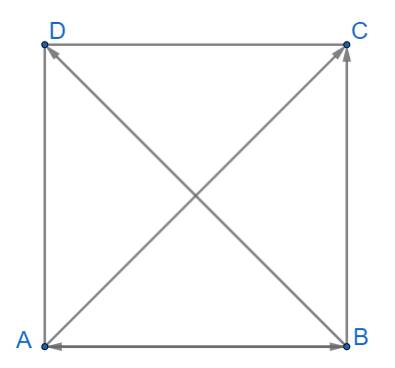
Ta có: \(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) \(AB \bot AD \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0\)
+) \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a\sqrt 2.\cos 45^\circ = a^2\)
+) \(\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.\cos 135^\circ = - {a^2}\)
+) \(AC \bot BD \Rightarrow \overrightarrow {AC} \bot \overrightarrow {BD} \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0\)
Chú ý
\(\overrightarrow {a} \bot \overrightarrow {b} \Leftrightarrow \overrightarrow {a} .\overrightarrow {b} = 0\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng 6 cm
Tính tích vô hướng \(\overrightarrow{AC.}\overrightarrow{BD}\)
ABCD là hình vuông
=>AC\(\perp\)BD
=>\(\overrightarrow{AC}\cdot\overrightarrow{BD}=0\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh 20 cm, M là trung điểm BC.Tính vô hướng →ab.→am
BM=BC/2=10cm
\(AM=\sqrt{20^2+10^2}=10\sqrt{5}\left(cm\right)\)
Xét ΔABM vuông tại B có sin BAM=BM/AM=10/10căn 5
nên cos BAM=2/căn 5
\(\overrightarrow{AB}\cdot\overrightarrow{AM}=AB\cdot AM\cdot cosBAM=20\cdot10\sqrt{5}\cdot\dfrac{2}{\sqrt{5}}\)
\(=20\cdot10\cdot2=40\cdot10=400\)
Đúng 2
Bình luận (0)
Cho hình chóp tứ giác S.ABCD có đáy là một hình vuông, độ dài tất cả các cạnh của hình chóp đã cho bằng a. Tính tích vô hướng \(\overrightarrow{SA}.\overrightarrow{SC}\)
Lời giải:$ABCD$ là hình vuông nên $AC=\sqrt{2}a$
Ta thấy: $SA^2+SC^2=a^2+a^2=2a^2=AC^2$
$\Rightarrow SAC$ là tam giác vuông tại $S$
$\Rightarrow \overrightarrow{SA}.\overrightarrow{SC}=0$
Đúng 1
Bình luận (0)
Cho hình thang ABCD vuông tạ A và D. AB=AD=a, CD=2a. Khi đó tích vô hướng \(\overrightarrow{AC}.\overrightarrow{BD}\)
\(\overrightarrow{AC}.\overrightarrow{BD}=\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AD}.\overrightarrow{BA}+\overrightarrow{AD}^2+\overrightarrow{DC}.\overrightarrow{BA}+\overrightarrow{DC}.\overrightarrow{AD}\)
\(=\overrightarrow{AD}^2-\overrightarrow{AB}.\overrightarrow{DC}=a^2-a.2a=-a^2\)
Đúng 3
Bình luận (2)
Cho hình vuông ABCD có cạnh 6aa) tính độ dài các vecto sau overrightarrow{u}overrightarrow{AB}-overrightarrow{AC} ; overrightarrow{v}overrightarrow{BC}+overrightarrow{BD}b) tính các tích vô hương sau : overrightarrow{AB}.overrightarrow{AC}; overrightarrow{BD}.overrightarrow{AC};overrightarrow{AB}.overrightarrow{CD}
Đọc tiếp
Cho hình vuông ABCD có cạnh = 6a
a) tính độ dài các vecto sau \(\overrightarrow{u}=\overrightarrow{AB}-\overrightarrow{AC}\) ; \(\overrightarrow{v}=\overrightarrow{BC}+\overrightarrow{BD}\)
b) tính các tích vô hương sau : \(\overrightarrow{AB}.\overrightarrow{AC}\); \(\overrightarrow{BD}.\overrightarrow{AC}\);\(\overrightarrow{AB}.\overrightarrow{CD}\)
a: AB=BC=CD=DA=6a
\(AC=BD=\sqrt{\left(6a\right)^2+\left(6a\right)^2}=6a\sqrt{2}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=6a\)
\(\left|\overrightarrow{BC}+\overrightarrow{BD}\right|=\sqrt{BC^2+BD^2+2\cdot BC\cdot BD\cdot cos45}\)
\(=\sqrt{36a^2+72a^2+\sqrt{2}\cdot6a\cdot6a\sqrt{2}}\)
\(=6a\sqrt{5}\)
b: \(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=6a\cdot6a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\)
\(=36a^2\)
Đúng 2
Bình luận (0)



