Cho hình hộp ABCDA'B'C'D" .Gọi điểm M thuộc các đường thẳng A'C sao cho vecto MA =-3 vecto MC . Đặt vecto BA= vecto a,vecto BB'= vecto b ,vectoBC =vecto c . Hãy biểu thị vecto BM qua các vecto a,b,c
Bài 1: Vectơ trong không gian
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O,gọi M,N,P theo thứ tự là trung điểm của các cạnh SB,SD,OC.
a. Tìm giao tuyến của (MNP) với (SAC)
b.Tìm giao điểm của SA với (MNP)
c. Tìm thiết diện (MNP) với hình chóp
Mn giải giúp em với :< cảm ơn trước..
a: P thuộc (MNP) giao (SAC)
Gọi E=SO giao MN
=>(MNP) giao (SAC)=PE
b: Chọn mp(SAC) có chứa SA
Gọi giao của PE với SA là G
=>G là giao điểm cần tìm
Đúng 0
Bình luận (0)
tại sao tích 2 VTCP = VTPT?
"Tại sao tích 2 vecto chỉ phương bằng 2 vecto pháp tuyến" ???
Đúng 0
Bình luận (0)
Lời giải:
Gọi cạnh bên đó là $SA$
$SA\perp AB, SA\perp AD\Rightarrow SA\perp (ABCD)$
$\Rightarrow (SAB)\perp (ABCD), (SAC)\perp (ABCD) , (SAD)\perp (ABCD)$
$AB, AD$ cùng vuông góc với nhau và vuông góc với giao tuyến $SA$ của 2 mp $(SAB)$ và $(SAD)$ nên $(SAD)\perp (SAB)$
Vậy có 4 cặp.
Đúng 1
Bình luận (1)
Cho hình lập phương ABCD.EFGH. Phân tích vecto AE theo vecto AC, AF, AH
\(\overrightarrow{AF}=\overrightarrow{AE}+\overrightarrow{AB}\)
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AH}=\overrightarrow{AE}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AF}-\overrightarrow{AC}+\overrightarrow{AH}=\overrightarrow{AE}+\overrightarrow{AB}-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AF}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AH}\)
Đúng 0
Bình luận (0)
Cho lăng trụ ABC.DEF có G,H,I,J,K lần lượt là trung điểm của AE, EC, CD, BC, BE. Chứng minh các vecto Ạ, GI, HK đồng phẳng
ACFD là hình bình hành \(\Rightarrow I\) đồng thời là trung điểm AF
\(\Rightarrow GI\) là đường trung bình tam giác AEF
\(\Rightarrow GI||BC\Rightarrow\overrightarrow{GI}\) có phương song song (ABC)
HK là đường trung bình tam giác EBC \(\Rightarrow HK||BC\)
\(\Rightarrow\overrightarrow{HK}\) có phương song song (ABC)
\(\Rightarrow AJ;GI;HK\) đều có phương song song (ABC) nên đồng phẳng
Đúng 0
Bình luận (0)
Cho tứ diện ABCD đều. Gọi G là trọng tâm của tam giác BCD.
a) Chứng minh AG\(\perp\) CD
b) Gọi M là trung điểm của CD . Tính góc giữa AC và BM .
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC .Góc giữa hai đường thẳng AB,BC
Cậu gán giá trị OA=OB=OC=1 và tình cho dễ nhé. Đặc biệt hóa ý
Đúng 0
Bình luận (0)
Do OA=OB=OC
\(\Rightarrow AB=AC=BC\)
\(\Rightarrow\Delta ABC\) đều
\(\Rightarrow\widehat{\left(AB;BC\right)}=\widehat{ABC}=60^0\)
Đúng 1
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a . Tính góc giữa 2 đường thẳng A'B và B'D'
\(BD||B'D'\Rightarrow\widehat{\left(A'B;B'D'\right)}=\widehat{\left(A'B;BD\right)}=\widehat{A'BD}\)
Mặt khác \(A'B=BD=A'D=a\sqrt{2}\) (đều là đường chéo của các hình vuông cạnh a)
\(\Rightarrow\Delta A'BD\) đều \(\Rightarrow\widehat{A'BD}=60^0\)
Đúng 0
Bình luận (0)
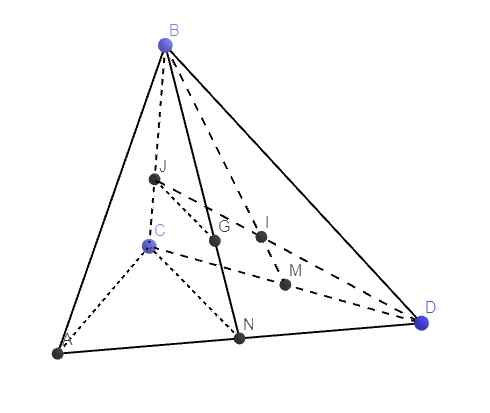
Mọi người ơi giúp mình với, mình ngồi cả ngày ko làm được :(( ( không xài meneliut nha )
\(IM=\dfrac{1}{4}IB\Rightarrow IM=\dfrac{1}{5}BM\Rightarrow\overrightarrow{MI}=\dfrac{1}{5}\overrightarrow{MB}=-\dfrac{1}{10}\left(\overrightarrow{BC}+\overrightarrow{BD}\right)\)
\(\Rightarrow\overrightarrow{DI}=\overrightarrow{DM}+\overrightarrow{MI}=\dfrac{1}{2}\overrightarrow{DC}-\dfrac{1}{10}\left(\overrightarrow{BC}+\overrightarrow{BD}\right)=\dfrac{1}{2}\overrightarrow{DB}+\dfrac{1}{2}\overrightarrow{BC}-\dfrac{1}{10}\overrightarrow{BC}-\dfrac{1}{10}\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{DI}=\dfrac{2}{5}\overrightarrow{BC}-\dfrac{3}{5}\overrightarrow{BD}\)
\(\overrightarrow{DJ}=\overrightarrow{DC}+\overrightarrow{CJ}=\overrightarrow{DB}+\overrightarrow{BC}+x.\overrightarrow{CB}=\left(1-x\right)\overrightarrow{BC}-\overrightarrow{BD}\)
D; I; J thẳng hàng \(\Rightarrow\dfrac{1-x}{\dfrac{2}{5}}=\dfrac{1}{\dfrac{3}{5}}\Rightarrow x=\dfrac{1}{3}\)
\(\Rightarrow CJ=\dfrac{1}{3}CB\Rightarrow BJ=\dfrac{2}{3}BC\Rightarrow\dfrac{BJ}{BC}=\dfrac{2}{3}\)
Gọi N là trung điểm AD \(\Rightarrow\dfrac{BG}{BN}=\dfrac{2}{3}\) (theo t/c trọng tâm)
\(\Rightarrow\dfrac{BJ}{BC}=\dfrac{BG}{BN}\Rightarrow JG||CN\)
\(\Rightarrow\widehat{\left(JG;CD\right)}=\widehat{\left(CN;CD\right)}=\widehat{NCD}=30^0\) (do tam giác ACD đều)
Đúng 0
Bình luận (0)