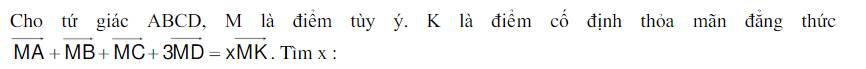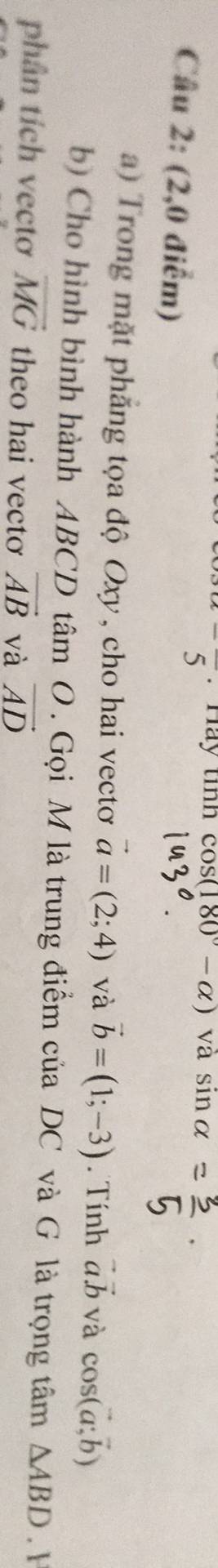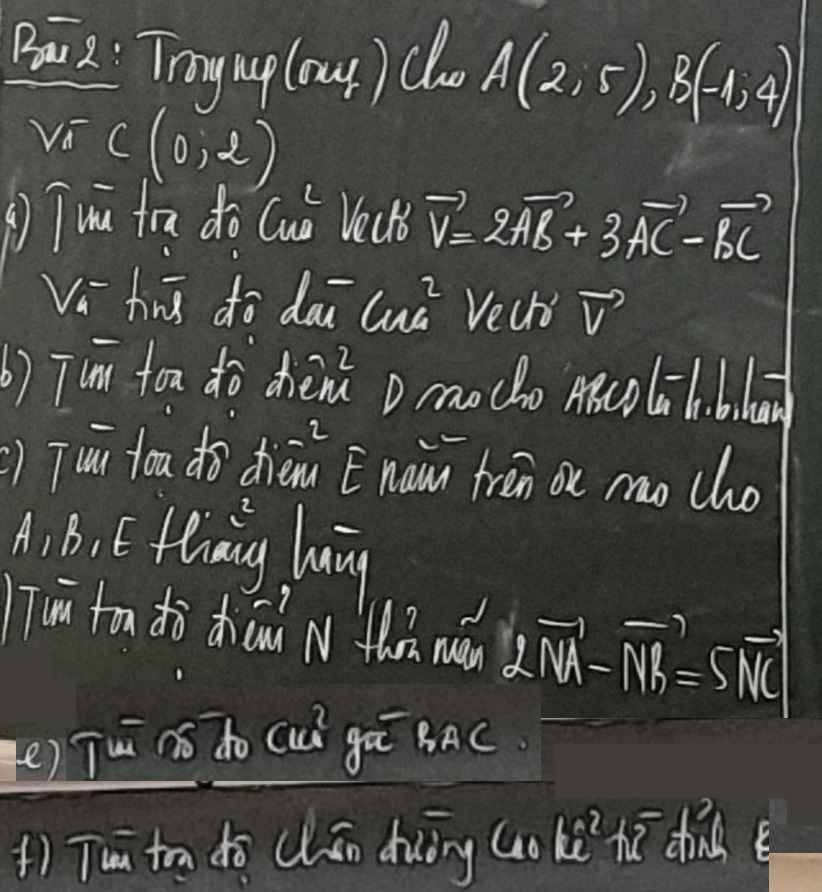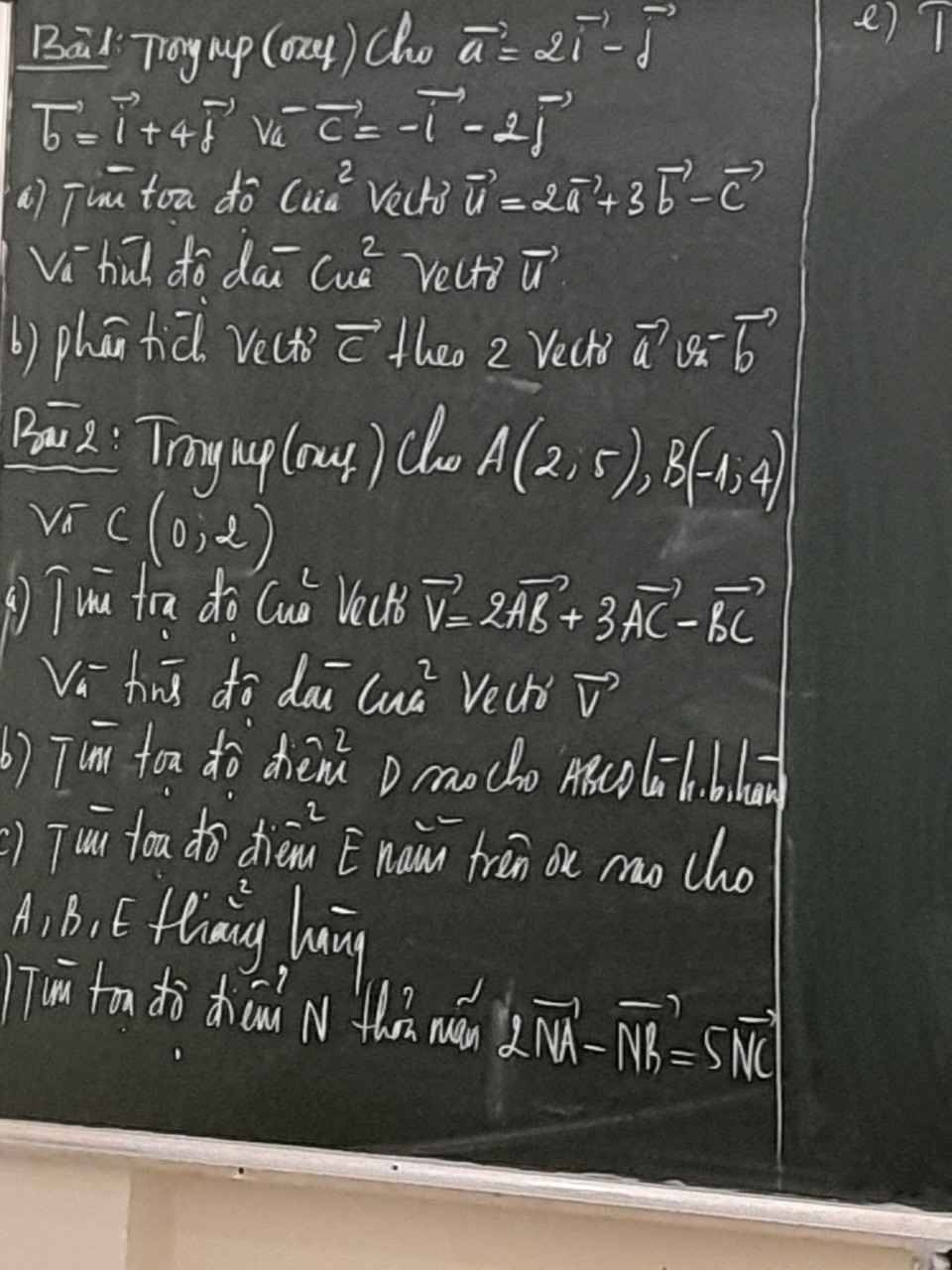Chương 1: VECTƠ

M là trung điểm BC \(\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)

\(\overrightarrow{IM}=2\overrightarrow{AI}\Rightarrow\overrightarrow{IA}+\overrightarrow{AM}=2\overrightarrow{AI}\)

\(\Rightarrow-\overrightarrow{AI}+\overrightarrow{AM}=2\overrightarrow{AI}\)

\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{3}\overrightarrow{AM}=\dfrac{1}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)

\(\overrightarrow{BI}=\overrightarrow{BA}+\overrightarrow{AI}=-\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}=-\dfrac{5}{6}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)

Đặt \(\overrightarrow{AK}=x.\overrightarrow{AC}\)

\(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}=-\overrightarrow{AB}+x.\overrightarrow{AC}\)

Do B, I, K thẳng hàng \(\Rightarrow\overrightarrow{BK}\) và \(BI\) cùng phương

\(\Rightarrow\dfrac{-1}{\left(-\dfrac{5}{6}\right)}=\dfrac{x}{\left(\dfrac{1}{6}\right)}\Rightarrow x=\dfrac{1}{5}\)

\(\Rightarrow\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AC}=\dfrac{1}{5}\left(\overrightarrow{AK}+\overrightarrow{KC}\right)=\dfrac{1}{5}\overrightarrow{AK}+\dfrac{1}{5}\overrightarrow{KC}\)

\(\Rightarrow\dfrac{4}{5}\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{KC}\)

\(\Rightarrow4.\overrightarrow{AK}=1.\overrightarrow{KC}\Rightarrow4.\overrightarrow{KA}=1.\overrightarrow{CK}\)

\(\Rightarrow\left\{{}\begin{matrix}n=4\\m=1\end{matrix}\right.\)

Các kí hiệu em ghi như IM=2AI và nKA=mCK nó là đoạn thẳng hay có vecto?

Xét hình thang ADCB có

Q,P lần lượt là trung điểm của AB,DC

=>QP là đường trung bình của hình thang ADCB

=>QP//AD//BC và \(QP=\dfrac{AD+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3}{4}BC\)

Ta có: M là trung điểm của BC

=>\(BM=MC=\dfrac{BC}{2}\)

Ta có: N là trung điểm của MC

=>\(MN=NC=\dfrac{MC}{2}=\dfrac{BC}{4}\)

BM+MN=BN

=>\(BN=\dfrac{1}{4}BC+\dfrac{1}{2}BC=\dfrac{3}{4}BC\)

=>QP=BN

Ta có: QP//BN

QP=BN

Do đó: \(\overrightarrow{QP}=\overrightarrow{BN}\)

=>Điểm E trùng với điểm P

Xét ΔABC có G là trọng tâm

nên \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)

\(\dfrac{1}{3}\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)\)

\(=\dfrac{1}{3}\left(\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right)\)

\(=\dfrac{1}{3}\left(3\cdot\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)

\(=\dfrac{1}{3}\cdot3\cdot\overrightarrow{MG}=\overrightarrow{MG}\)

Lời giải:

\(A=|3\overrightarrow{OA}+4\overrightarrow{OB}|\\ \Rightarrow A^2=9OA^2+16OB^2+24\overrightarrow{OA}.\overrightarrow{OB}\)

\(A^2=9a^2+16.2a^2+\overrightarrow{OA}(\overrightarrow{OA}+\overrightarrow{AB})=41a^2+OA^2+\overrightarrow{OA}.\overrightarrow{AB}\\ =41a^2+a^2+0=42a^2\)

(do $OA, AB$ vuông góc với nhau)

$\Rightarrow A=\sqrt{42}a$

a: A(-2;1); B(3;2); C(-1;4)

\(AB=\sqrt{\left(3+2\right)^2+\left(2-1\right)^2}=\sqrt{5^2+1^2}=\sqrt{26}\)

\(AC=\sqrt{\left(-1+2\right)^2+\left(4-1\right)^2}=\sqrt{1^2+3^2}=\sqrt{10}\)

\(BC=\sqrt{\left(-1-3\right)^2+\left(4-2\right)^2}=\sqrt{2^2+\left(-4\right)^2}=2\sqrt{5}\)

Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{26+10-20}{2\cdot\sqrt{26}\cdot\sqrt{10}}=\dfrac{4}{\sqrt{65}}\)

=>\(sinBAC=\sqrt{1-cos^2BAC}=\dfrac{7}{\sqrt{65}}\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)

\(=\dfrac{1}{2}\cdot\dfrac{7}{\sqrt{65}}\cdot\sqrt{26}\cdot\sqrt{10}=7\)

b: ADBC là hình thoi

=>AB\(\perp\)DC và \(\overrightarrow{AD}=\overrightarrow{CB}\)

=>\(\left\{{}\begin{matrix}\overrightarrow{AD}=\overrightarrow{CB}\\\overrightarrow{AB}\cdot\overrightarrow{DC}=0\end{matrix}\right.\)

\(\overrightarrow{AD}=\left(x+2;y-1\right);\overrightarrow{CB}=\left(4;-2\right)\)

\(\overrightarrow{AB}=\left(5;1\right);\overrightarrow{DC}=\left(-1-x;4-y\right)\)

Do đó, ta có: \(\left\{{}\begin{matrix}x+2=4\\y-1=-2\\5\left(-x-1\right)+1\left(4-y\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=-1\\5\left(-2-1\right)+1\left(4+1\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=2\\y=-1\\5\cdot\left(-3\right)+1\cdot5=0\left(sai\right)\end{matrix}\right.\)

vậy: Không có điểm D nào thỏa mãn

Vì đẳng thức đã cho thỏa mãn với mọi M

Xét trường hợp M trùng K

\(\Rightarrow\overrightarrow{KA}+\overrightarrow{KB}+\overrightarrow{KC}+3\overrightarrow{KD}=x.\overrightarrow{KK}=\overrightarrow{0}\)

Gọi G là trọng tâm tam giác ABC

\(\Rightarrow3\left(\overrightarrow{KG}+\overrightarrow{KD}\right)=\overrightarrow{0}\)

=> K là trung điểm DG

Mà: \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+3\overrightarrow{MD}=x.\overrightarrow{MK}\)

\(\Rightarrow3\left(\overrightarrow{MG}+\overrightarrow{MD}\right)=x.\overrightarrow{MK}\)

\(\Leftrightarrow6.\overrightarrow{MK}=x.\overrightarrow{MK}\)

\(\Rightarrow x=6\)

b: Gọi giao điểm của BG với AD là K, E là giao điểm của DG với AB

Xét ΔABD có

G là trọng tâm

K là giao điểm của BG với AD

E là giao điểm của DG với AB

Do đó: K là trung điểm của AD và E là trung điểm của AB

Xét ΔABD có

G là trọng tâm của ΔABD

AO là đường trung tuyến

Do đó: \(AG=\dfrac{2}{3}\cdot AO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AC=\dfrac{1}{3}\cdot AC\)

AG+GC=AC

=>\(GC+\dfrac{1}{3}AC=AC\)

=>\(GC=\dfrac{2}{3}AC\)

Xét ΔDAB có 

G là trọng tâm

DE là đường trung tuyến

Do đó; \(DG=\dfrac{2}{3}DE\)

Xét ΔGDC có GM là trung tuyến

nên \(\overrightarrow{GM}=\dfrac{1}{2}\left(\overrightarrow{GD}+\overrightarrow{GC}\right)\)

\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{DE}+\dfrac{2}{3}\cdot\overrightarrow{AC}\right)\)

\(=\dfrac{1}{3}\left(-\overrightarrow{DE}+\overrightarrow{AC}\right)\)

\(=\dfrac{1}{3}\left(-\dfrac{1}{2}\cdot\left(\overrightarrow{DA}+\overrightarrow{DB}\right)+\overrightarrow{AB}+\overrightarrow{AD}\right)\)

\(=\dfrac{1}{3}\left(\dfrac{1}{2}\overrightarrow{AD}-\dfrac{1}{2}\overrightarrow{DB}+\overrightarrow{AB}+\overrightarrow{AD}\right)\)

\(=\dfrac{1}{3}\left(\dfrac{3}{2}\overrightarrow{AD}-\dfrac{1}{2}\left(\overrightarrow{DA}+\overrightarrow{AB}\right)+\overrightarrow{AB}\right)\)

\(=\dfrac{1}{3}\left(\dfrac{3}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AD}-\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AB}\right)\)

\(=\dfrac{1}{3}\left(2\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\right)\)

\(=\dfrac{2}{3}\overrightarrow{AD}+\dfrac{1}{6}\overrightarrow{AB}\)

a: \(\overrightarrow{a}=\left(2;4\right);\overrightarrow{b}=\left(1;-3\right)\)

=>\(\overrightarrow{a}\cdot\overrightarrow{b}=2\cdot1+4\cdot\left(-3\right)=-10\)

\(\left|\overrightarrow{a}\right|=\sqrt{2^2+4^2}=2\sqrt{10}\)

\(\left|\overrightarrow{b}\right|=\sqrt{1^2+\left(-3\right)^2}=\sqrt{10}\)

\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\overrightarrow{b}}=\dfrac{-10}{2\sqrt{10}\cdot\sqrt{10}}=-\dfrac{1}{2}\)

=>\(\left(\overrightarrow{a};\overrightarrow{b}\right)=120^0\)

MNPQ là hình bình hành tâm I

=>I là trung điểm chung của MP và NQ

Xét ΔKQN có KI là trung tuyến

nên \(\overrightarrow{KQ}+\overrightarrow{KN}=2\cdot\overrightarrow{KI}\)

Xét ΔKMP có KI là đường trung tuyến

nên \(\overrightarrow{KM}+\overrightarrow{KP}=2\cdot\overrightarrow{KI}\)

mà \(\overrightarrow{KQ}+\overrightarrow{KN}=2\cdot\overrightarrow{KI}\)

nên \(\overrightarrow{KM}+\overrightarrow{KP}+\overrightarrow{KQ}+\overrightarrow{KN}=2\overrightarrow{KI}+2\overrightarrow{KI}=4\overrightarrow{KI}\)

a: A(2;5); B(-1;4); C(0;2)

Tọa độ vecto AB là:

\(\left\{{}\begin{matrix}x=-1-2=-3\\y=4-5=-1\end{matrix}\right.\)

Tọa độ vecto AC là:

\(\left\{{}\begin{matrix}x=0-2=-2\\y=2-5=-3\end{matrix}\right.\)

Tọa độ vecto BC là:

\(\left\{{}\begin{matrix}x=0-\left(-1\right)=1\\y=2-4=-2\end{matrix}\right.\)

Vậy: \(\overrightarrow{AB}=\left(-3;-1\right);\overrightarrow{AC}=\left(-2;-3\right);\overrightarrow{BC}=\left(1;-2\right)\)

\(\overrightarrow{V}=2\overrightarrow{AB}+3\overrightarrow{AC}-\overrightarrow{BC}\)

=>\(\overrightarrow{V}=\left(2\cdot\left(-3\right)+3\left(-2\right)-1;2\cdot\left(-1\right)+3\left(-3\right)-\left(-2\right)\right)\)

=>\(\overrightarrow{V}=\left(-13;-9\right)\)

\(\left|\overrightarrow{V}\right|=\sqrt{\left(-13\right)^2+\left(-9\right)^2}=\sqrt{198}=9\sqrt{22}\)

b: ABCD là hình bình hành

=>\(\overrightarrow{AB}=\overrightarrow{DC}\)

mà \(\overrightarrow{AB}=\left(-3;-1\right);\overrightarrow{DC}=\left(-x;2-y\right)\)

nên \(\left\{{}\begin{matrix}-x=-3\\2-y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)

Vậy: D(3;3)

c: E nằm trên tia Ox nên E(x;0)

\(\overrightarrow{AB}=\left(-3;-1\right);\overrightarrow{AE}=\left(x-2;-5\right)\)

A,B,E thẳng hàng nên \(\dfrac{x-2}{-3}=\dfrac{-5}{-1}=5\)

=>x-2=-15

=>x=-15+2=-13

vậy: E(-13;0)

d: \(\overrightarrow{NA}=\left(2-x;5-y\right);\overrightarrow{NB}=\left(-1-x;4-y\right);\overrightarrow{NC}=\left(-x;2-y\right)\)

\(2\overrightarrow{NA}-\overrightarrow{NB}=5\overrightarrow{NC}\)

=>\(\left\{{}\begin{matrix}2\left(2-x\right)-\left(-1-x\right)=5\left(-x\right)\\2\left(5-y\right)-\left(4-y\right)=5\left(2-y\right)\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4-2x+x+1=-5x\\10-2y-4+y=10-5y\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-5x=-x+5\\-5y+10=-y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x=5\\-4y=-4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-\dfrac{5}{4}\\y=1\end{matrix}\right.\)

Vậy: \(N\left(-\dfrac{5}{4};1\right)\)

e: \(AB=\sqrt{\left(-3\right)^2+\left(-1\right)^2}=\sqrt{10}\)

\(AC=\sqrt{\left(-2\right)^2+\left(-3\right)^2}=\sqrt{13}\)

\(BC=\sqrt{1^2+\left(-2\right)^2}=\sqrt{5}\)

Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{10+13-5}{2\cdot\sqrt{10}\cdot\sqrt{13}}\)

\(=\dfrac{18}{2\sqrt{130}}=\dfrac{9}{\sqrt{130}}\)

=>\(sinBAC=\sqrt{1-\left(\dfrac{9}{\sqrt{130}}\right)^2}=\dfrac{7}{\sqrt{130}}\)

Bài 1:

a: \(\overrightarrow{a}=2\overrightarrow{i}-\overrightarrow{j};\overrightarrow{b}=\overrightarrow{i}+4\overrightarrow{j};c=-\overrightarrow{i}-2\overrightarrow{j}\)

=>\(\overrightarrow{a}=\left(2;-1\right);\overrightarrow{b}=\left(1;4\right);\overrightarrow{c}=\left(-1;-2\right)\)

\(\overrightarrow{u}=2\cdot\overrightarrow{a}+3\cdot\overrightarrow{b}-\overrightarrow{c}\)

=>\(\overrightarrow{u}=\left(2\cdot2+3\cdot1-\left(-1\right);2\cdot\left(-1\right)+3\cdot4-\left(-2\right)\right)\)

=>\(\overrightarrow{u}=\left(8;12\right)\)

\(\left|\overrightarrow{u}\right|=\sqrt{8^2+12^2}=\sqrt{144+64}=\sqrt{208}=4\sqrt{13}\)

b: Đặt \(\overrightarrow{c}=x\cdot\overrightarrow{a}+y\cdot\overrightarrow{b}\)

\(\overrightarrow{a}=\left(2;-1\right);\overrightarrow{b}=\left(1;4\right);\overrightarrow{c}=\left(-1;-2\right)\)

=>\(\left\{{}\begin{matrix}-1=x\cdot2+y\cdot1\\-2=x\cdot\left(-1\right)+4y\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x+y=-1\\-x+4y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=-1\\-2x+8y=-4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}9y=-5\\x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{5}{9}\\x=4y+2=4\cdot\left(-\dfrac{5}{9}\right)+2=-\dfrac{20}{9}+2=-\dfrac{2}{9}\end{matrix}\right.\)

vậy: \(\overrightarrow{c}=\dfrac{-2}{9}\cdot\overrightarrow{a}+\dfrac{-5}{9}\cdot\overrightarrow{b}\)