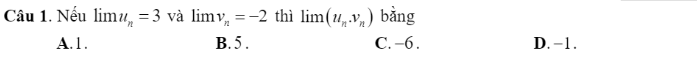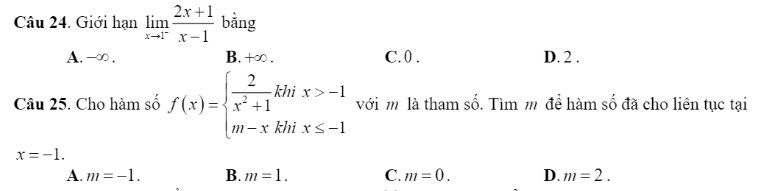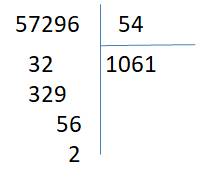trình bày hộ câu này với ạ/; 355 x 45 + 54 x 355 + 355 =
DL
Những câu hỏi liên quan
Bạn nào giải giúp mình hai câu này vs ạ , trình bày hộ mình với , mình cám ơn ạ
22/ \(\omega A=8\pi\)
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Leftrightarrow A^2=3,2^2+\dfrac{\left(4,8\pi\right)^2}{\omega^2}\)
\(\Leftrightarrow\omega^2A^2=3,2^2\omega^2+23,04\pi^2\Leftrightarrow64\pi^2=3,2^2.\omega^2+23,04\pi^2\Leftrightarrow\omega=2\pi\left(rad/s\right)\)
\(\Rightarrow f=\dfrac{\omega}{2\pi}=\dfrac{2\pi}{2\pi}=1\left(Hz\right)\Rightarrow D.1Hz\)
23/ \(\omega A=20;\omega^2A=80\Rightarrow\left\{{}\begin{matrix}\omega=4\left(rad/s\right)\\A=5cm\end{matrix}\right.\)
\(\Rightarrow v=\omega\sqrt{A^2-x^2}=4.\sqrt{5^2-4^2}=12\left(cm/s\right)\Rightarrow A.12cm/s\)
Đúng 1
Bình luận (0)
Là xem naruto
làm giúp em đề hoá này với ạ và câu 31 32 trình bày tự luận hộ em em cảm ơn

ai trả lời hộ mik câu này với ạ 57296 chia cho 54 bằng bao? nhiêu và cách trình bày sao cho đúng ạ mik cảm ơn mn rất nhiều !!!
Viết đoạn văn 100 chữ trình bày suy nghĩ của iem zề đức tính tự lập UvU.
bác nào giỏi hộ iem câu này với,sắp hết tết rồi mà em vx chưa lm xong bt Văn đây này. Xin cảm ơn nhiều ạ!
Em tham khảo nhé !!
Tính tự lập có một vai trò vô cùng quan trọng trong cuộc sống của mỗi con người. Vậy tính tự lập là gì? Tính tự lập là sự tự ý thức của con người khi làm một việc gì đó mà không cần sự nhắc nhớ, đôn đốc hay dựa dẫm và người khác. Người có tính tự lập luôn luôn là người đạt nhiều thành công trong cuộc sống. Thực tế cho chúng ta thấy có rất nhiều người có tính tự lập. Như Jack Ma, nhờ có tính tự lập mà ông đã trở thành tỉ phú. Thử hỏi xem nếu không có tính tự lập thì chúng ta sẽ làm được gì? Sẽ đạt được thành công, sẽ bước trên con đường trải đầy hoa hay không? Tính tự lập giúp chúng ta có động lực để làm việc. Có tự lập, chúng ta mới biết được ngoài kia có biết bao sóng gió, thử thách. Nếu không có tự lập, bạn sẽ chẳng bao giờ làm được việc gì thậm chí hình thành thói ỷ lại, dựa dẫm vào người khác. Hiện nay, có rất nhiều các bậc phụ huynh rất nuông chiều con, không cho con sống tự lập để rồi gây ra nhiều hậu quả đáng tiếc. Tuy nhiên, không phải lúc nào chúng ta cũng tự lập. Đôi lúc chúng ta vẫn phải hỏi ý kiến của người lớn, những người thân trong gia đình để có hướng đi tốt nhất cho chính bản thân mình. Thật vậy, mỗi người hãy rèn cho mình tính tự lập bới tự lập không phải tự có, xuất hiện trong chúng ta, nó chỉ có khi chúng ta biết trau dồi, biết rèn luyện mà thôi!
Đúng 1
Bình luận (1)
Tự lập là một trong những yếu tố quan trọng hàng đầu dẫn đến sự thành công của con người. Tự lập là chúng ta có khả năng tự xây dựng lấy cuộc sống cho mình, không ỉ lại, không nhờ vả người khác. Nó thể hiện sự tự tin của bản thân ta. Tính tự lập còn giúp cho ta rèn luyện những phẩm chất đạo đức tốt đẹp khác nữa như: cần cù, chịu khó, kiên nhẫn,…Giúp cho ta dần dần hoàn thiện trong cuộc sống. Bên cạnh đó, tính tự lập còn tạo cho bản thân những thử thách mới lạ, tạo niềm vui cho cuộc sống. Có tính tự lập thì chúng ta sẽ có được một cuộc sống tốt đẹp hơn. Tự lập là một đức tính rất tốt, quý báu. Chúng ta cần phải rèn luyện, trau dồi, bồi dưỡng đức tính quý báu này để ta có thể đương đầu một cách tự tin trước cuộc đời đầy bon chen xô bồ này.
Đúng 1
Bình luận (0)
Trình bày câu này giúp mình với ạ !!
Trình bày lời giải mấy câu này giúp em với ạ

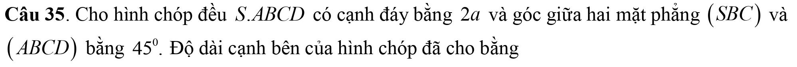
34:
(SBA) giao (SCD)=d đi qua S, d//AB//CD
=>d vuông góc SA,d vuông góc SD
=>(SAB;SCD)=(SA;SD)
tan ASD=AD/AS=1/căn 3
=>góc ASD=30 độ
Đúng 0
Bình luận (0)
Trình bày cách giải mấy câu này giúp mình với ạ :((( khó quá


15.
\(\Delta'=m^2+m-2>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\)
Đáp án B
16.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow\dfrac{\pi}{4}< \dfrac{a}{2}< \dfrac{\pi}{2}\Rightarrow\dfrac{\sqrt{2}}{2}< sin\dfrac{a}{2}< 1\Rightarrow\dfrac{1}{2}< sin^2\dfrac{a}{2}< 1\)
\(sina=\dfrac{3}{5}\Leftrightarrow sin^2a=\dfrac{9}{25}\Leftrightarrow4sin^2\dfrac{a}{2}.cos^2\dfrac{a}{2}=\dfrac{9}{25}\)
\(\Leftrightarrow sin^2\dfrac{a}{2}\left(1-sin^2\dfrac{a}{2}\right)=\dfrac{9}{100}\Leftrightarrow sin^4\dfrac{a}{2}-sin^2\dfrac{a}{2}+\dfrac{9}{100}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2\dfrac{a}{2}=\dfrac{1}{10}< \dfrac{1}{2}\left(loại\right)\\sin^2\dfrac{a}{2}=\dfrac{9}{10}\end{matrix}\right.\)
\(\Rightarrow sin\dfrac{a}{2}=\dfrac{3\sqrt{10}}{10}\)
Đúng 3
Bình luận (0)
17.
Áp dụng công thức trung tuyến:
\(AM=\dfrac{\sqrt{2\left(AB^2+AC^2\right)-BC^2}}{2}=\dfrac{\sqrt{201}}{2}\)
18.
\(\Leftrightarrow x^2+2x+4>m^2+2m\) ; \(\forall x\in\left[-2;1\right]\)
\(\Leftrightarrow m^2+2m< \min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)\)
Xét \(f\left(x\right)=x^2+2x+4\) trên \(\left[-2;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-2;1\right]\) ; \(f\left(-2\right)=4\) ; \(f\left(-1\right)=3\) ; \(f\left(1\right)=7\)
\(\Rightarrow\min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)=f\left(1\right)=3\)
\(\Rightarrow m^2+2m< 3\Leftrightarrow m^2+2m-3< 0\)
\(\Rightarrow-3< m< 1\Rightarrow m=\left\{-2;-1;0\right\}\)
Đáp án C
Đúng 3
Bình luận (0)
19. Hình đa giác là bát giác đều như hình vẽ

\(S=8S_{OAB}=8.\dfrac{1}{2}.IB.OA=4.y_B.x_A=4.\dfrac{\sqrt{2}}{2}.1=2\sqrt{2}\)
Cả 4 đáp án đều không chính xác?
20.
\(M\in\Delta\Rightarrow a+b+1=0\Rightarrow b=-a-1\Rightarrow M\left(a;-a-1\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AM}=\left(a+1;-a-4\right)\\\overrightarrow{BM}=\left(a-1;-a-2\right)\end{matrix}\right.\)
\(AM+BM=\sqrt{\left(a+1\right)^2+\left(-a-4\right)^2}+\sqrt{\left(-a-2\right)^2+\left(a-1\right)^2}\)
\(AM+BM\ge\sqrt{\left(a+1-a-2\right)^2+\left(-a-4+a-1\right)^2}=\sqrt{26}\)
Dấu "=" xảy ra khi:
\(\left(a+1\right)\left(a-1\right)=\left(-a-4\right)\left(-a-2\right)\Leftrightarrow a=-\dfrac{3}{2}\Rightarrow b=\dfrac{1}{2}\)
\(\Rightarrow ab=-\dfrac{3}{4}\)
Đúng 3
Bình luận (5)
Mọi người trình bày cách giải mấy câu này giúp em với ạ!!
Đọc tiếp
Mọi người trình bày cách giải mấy câu này giúp em với ạ!!

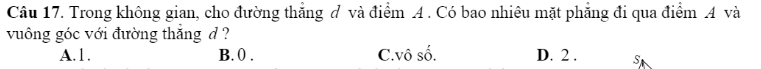
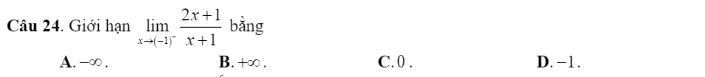

2.B (t/c của giới hạn)
6.B H/s ko x/đ với x = 0 -> Ko liên tục tại đ x = 0
17.C
24. \(\lim\limits_{x\rightarrow\left(-1\right)^-}\dfrac{2x+1}{x+1}\) . Thấy : \(\lim\limits_{x\rightarrow\left(-1\right)^-}2x+1=2.\left(-1\right)+1=-1\)
\(\lim\limits_{x\rightarrow\left(-1\right)^-}x+1=0\) ; \(x\rightarrow\left(-1\right)^-\Rightarrow x+1< 0\).
Do đó : \(\lim\limits_{x\rightarrow\left(-1\right)^-}=+\infty\) . Chọn B
Đúng 3
Bình luận (0)
33 . B
Trên (SAB) ; Lấy H là TĐ của AB ; ta có : SH \(\perp AB\) ( \(\Delta SAB\) đều ) ; HC \(\perp AB\) ( \(\Delta ABC\) đều )
Ta có : (SAB) \(\perp\left(ABC\right)\) ; \(\left(SAB\right)\cap\left(ABC\right)=AB;SH\perp AB\)
\(\Rightarrow SH\perp\left(ABC\right)\)
\(SC\cap\left(ABC\right)=C\) . Suy ra : \(\left(SC;\left(ABC\right)\right)=\widehat{SCH}\)
Có : \(SH\perp HC\) => \(\Delta SHC\) vuông tại H
G/s \(\Delta\)ABC đều có cạnh là a \(\Rightarrow AB=a\)
\(\Delta SAB\) đều => SA = SB = AB = a
Tính được : \(SH=HC=\dfrac{\sqrt{3}}{2}a\)
\(\Delta SHC\) vuông tại H : \(tan\widehat{SCH}=\dfrac{SH}{HC}=1\)
\(\Rightarrow\widehat{SCH}=45^o\) => ...
Đúng 3
Bình luận (0)
Trình bày lời giải mấy câu này giúp em với ạ!! Em xin cảm ơn.
Đọc tiếp
Trình bày lời giải mấy câu này giúp em với ạ!! Em xin cảm ơn.